1、什么是高斯混合模型[1]
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。
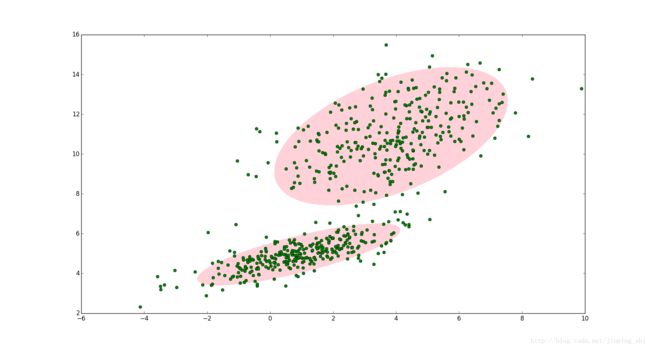
如图1,图中的点在我们看来明显分成两个聚类。这两个聚类中的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM,那么只能用一个的二维高斯分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理,毕竟肉眼一看就觉得应该把它们分成两类。
这时候就可以使用GMM了!如图2,数据在平面上的空间分布和图1一样,这时使用两个二维高斯分布来描述图2中的数据,分别记为N(μ1,Σ1)和N(μ2,Σ2) 。图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布N(μ1,Σ1)和N(μ2,Σ2) 合成一个二维的分布,那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合,用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型(GMM)。
高斯混合模型(GMM)的数学表示:
2、什么是EM算法[2]
期望极大(Expectation Maximization)算法,也称EM算法,是一种迭代算法,由Dempster et. al 在1977年提出,用于含有隐变量的概率参数模型的极大似然估计。
EM算法作为一种数据添加算法,在近几十年得到迅速的发展,主要源于当前科学研究以及各方面实际应用中数据量越来越大的情况下,经常存在数据缺失或者不可用的的问题,这时候直接处理数据比较困难,而数据添加办法有很多种,常用的有神经网络拟合、添补法、卡尔曼滤波法等,但是EM算法之所以能迅速普及主要源于它算法简单,稳定上升的步骤能相对可靠地找到“最优的收敛值”。
(个人的理解就是用含有隐变量的含参表达式不断拟合,最终能收敛并拟合出不含隐变量的含参表达式)
模型的EM训练过程,直观的来讲是这样:我们通过观察采样的概率值和模型概率值的接近程度,来判断一个模型是否拟合良好。然后我们通过调整模型以让新模型更适配采样的概率值。反复迭代这个过程很多次,直到两个概率值非常接近时,我们停止更新并完成模型训练。现在我们要将这个过程用算法来实现,所使用的方法是模型生成的数据来决定似然值,即通过模型来计算数据的期望值。通过更新参数μ和σ来让期望值最大化。这个过程可以不断迭代直到两次迭代中生成的参数变化非常小为止。该过程和k-means的算法训练过程很相似(k-means不断更新类中心来让结果最大化),只不过在这里的高斯模型中,我们需要同时更新两个参数:分布的均值和标准差.[3]
3、GMM和EM的使用[1,3]
GMM常用于聚类。如果要从 GMM 的分布中随机地取一个点的话,实际上可以分为两步:首先随机地在这 K 个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数Πk ,选中 Component 之后,再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布,转化为已知的问题。
根据数据来推算概率密度通常被称作 density estimation 。特别地,当我已知(或假定)概率密度函数的形式,而要估计其中的参数的过程被称作『参数估计』。
(推导和迭代收敛过程这里省略,可参考资料1)
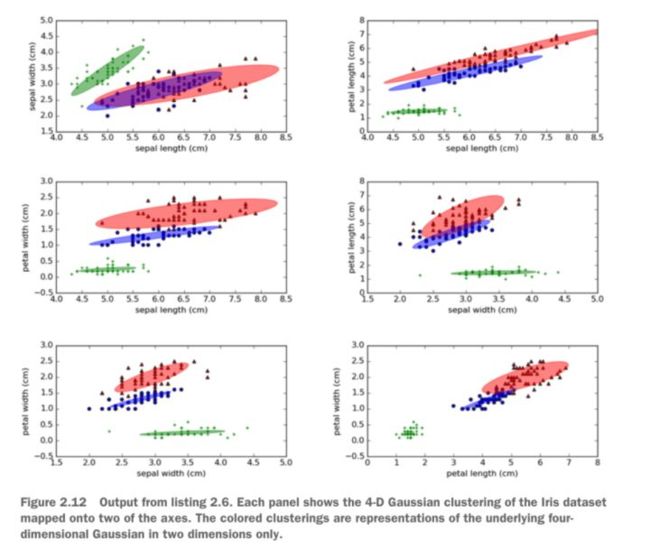
一个实际的例子:用GMM对iris数据集进行聚类,并通过make_ellipses表示出来
make_ellipses方法概念上很简单,它将gmm对象(训练模型)、坐标轴、以及x和y坐标索引作为参数,运行后基于指定的坐标轴绘制出相应的椭圆图形。
4、k-means和GMM的关系[3]
在特定条件下,k-means和GMM方法可以互相用对方的思想来表达。在k-means中根据距离每个点最接近的类中心来标记该点的类别,这里存在的假设是每个类簇的尺度接近且特征的分布不存在不均匀性。这也解释了为什么在使用k-means前对数据进行归一会有效果。高斯混合模型则不会受到这个约束,因为它对每个类簇分别考察特征的协方差模型。
K-means算法可以被视为高斯混合模型(GMM)的一种特殊形式。整体上看,高斯混合模型能提供更强的描述能力,因为聚类时数据点的从属关系不仅与近邻相关,还会依赖于类簇的形状。n维高斯分布的形状由每个类簇的协方差来决定。在协方差矩阵上添加特定的约束条件后,可能会通过GMM和k-means得到相同的结果。
在k-means方法中使用EM来训练高斯混合模型时对初始值的设置非常敏感。而对比k-means,GMM方法有更多的初始条件要设置。实践中不仅初始类中心要指定,而且协方差矩阵和混合权重也要设置。可以运行k-means来生成类中心,并以此作为高斯混合模型的初始条件。由此可见并两个算法有相似的处理过程,主要区别在于模型的复杂度不同。
5、总结
高斯混合模型的基本假设是已知类别的比例和类别的个数,但是不知道每个样例的具体标签,据此用EM的模式为每个样本进行最优的标注。也就是说它适合的是无标签学习的分类问题,并且需要已知基本假设。
整体来看,所有无监督机器学习算法都遵循一条简单的模式:给定一系列数据,训练出一个能描述这些数据规律的模型(并期望潜在过程能生成数据)。训练过程通常要反复迭代,直到无法再优化参数获得更贴合数据的模型为止。
【1】https://blog.csdn.net/jinping_shi/article/details/59613054 高斯混合模型(GMM)及其EM算法的理解
【2】https://cloud.tencent.com/developer/news/231599 机器学习中的数学(4)-EM算法与高斯混合模型(GMM)
【3】https://zhuanlan.zhihu.com/p/31103654 一文详解高斯混合模型原理