星期五的晚上,一帮同事在希格玛大厦附近的“硬盘酒吧”多喝了几杯。程序员多喝了几杯之后谈什么呢?自然是算法问题。有个同事说:“我以前在餐馆打工,顾客经常点非常多的烙饼。店里的饼大小不一,我习惯在到达顾客饭桌前,把一摞饼按照大小次序摆好——小的在上面,大的在下面。由于我一只手托着盘子,只好用另一只手,一次抓住最上面的几块饼,把它们上下颠倒个个儿,反复几次之后,这摞烙饼就排好序了。我后来想,这实际上是个有趣的排序问题:假设有n块大小不一的烙饼,那最少要翻几次,才能达到最后大小有序的结果呢?你能否写出一个程序,对于n块大小不一的烙饼,输出最优化的翻饼过程呢?
我们首先将问题简化一下,简化问题可以然我们集中精力在问题的本质上。我们假设就是10个烙饼,大小用1-10来表示,用一个数组存储,数组的下标表示相对位置关系。翻转烙饼就是将到数组中的0到i的元素的顺序调转,通过翻转操作,最后要数组是增序的。
先不考虑最优解的情况,先尝试着通过翻转,让数组排好序。很容易想到的是汉罗塔中的思路,先将最底下面的放好,再考虑上面的。通过递归来解决。将最大的烙饼放在最下面,可能的情况是:
1)最大的烙饼本身就在最下面,我们不用任何操作;
2)最大的烙饼在最上面,我们将所有烙饼一起翻转一下就可以了;
3)最大的烙饼在中间,那么我们先将烙饼所在位置上面包括该烙饼本身一起翻转一次,最大的烙饼就在最上面了,再如2)中一样操作。
将最大烙饼放好位置后,再考虑倒数第二个。重复上面的操作,最终可以完成对烙饼的排序。
这个方案中,对每个位置的调整,翻转次数为0,1或2。所以最多2*n次,我们就可以完成排序,再考虑上面的第一个位置,实际上,我们完成了第二个位置的排序时,最小的烙饼已经排好序了(和蜗牛爬电线杆类似)。实现就是还可以考虑第三个位置排好序了,最上面的两个烙饼最多需要一次翻转就可以了。所以最多次数为max(2n-3,0),考虑到n=1的情况,我们用个max。
好了,我们知道了排序的一个解决方案了,但是我们不知道是不是最优解。要知道最有解,最直接的办法是找到所有解,然后比较翻转次数。
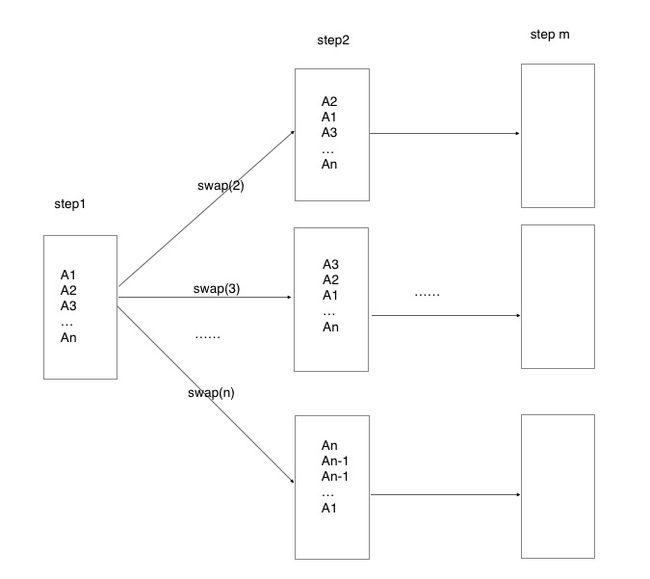
如何找到所有解呢,很暴力的想法就是穷举。将所有翻转方案列举一下,找到能够排序的。
上图中演示了,怎样遍历所有翻转情况。但似乎好像有点问题。很明显上面的过程是个递归过程,但是没有看到递归的出口。我们分析一下出口情况:
1)我们知道了至少有一种方案的翻转次数是小于max(2n-3,0)的,那么最优方案肯定也小于这个值,所以第一个出口是step > max(2n-3,0)的时候,一点不是最优的,不用继续了。拓展一下,最佳方案的翻转次数不会大于目前已经找到的最佳方案的翻转次数,所以出口条件为,step > maxStep,maxStep为目前找到的最佳方案翻转次数。
2)目前,已经排好序了,找到了方案,不需要继续了。退出前更新maxStep。
用上述两个条件,我们已经可以给出初步的解决方案了。代码如下:
class CakeSwap
{
private:
int swapCount;
int cakeArray[10] = {7,3,6,8,5,2,1,4,9,10};
int *swapArray;
int *tempSwapArray;
public:
void init(){
swapCount = 20;//最多翻转次数
swapArray = new int[20];
tempSwapArray = new int[20];
search(0);
printResult();
}
void search(int step)
{
if(step > swapCount)
{
return;
}
if(isSorted(10))
{
if (swapCount > step)
{
swapCount = step;
for (int index = 0 ; index < step ; index ++)
{
swapArray[index] = tempSwapArray[index];
}
}
return;
}
for(int index = 1; index < 10 ; index++)
{
swap(index, cakeArray, 10);
tempSwapArray[step] = index;
search(step + 1);
swap(index, cakeArray, 10);
}
}
bool isSorted(int size)
{
for(int i = 0; i < size - 1; i++)
{
if(cakeArray[i] > cakeArray[i + 1])
{
return false;
}
}
return true;
}
void swap(int i, int *array, int size)
{
if (i < size)
{
for (int beginIndex = 0 , endIndex = i; beginIndex < endIndex ; beginIndex++, endIndex--)
{
array[beginIndex] = array[beginIndex] + array[endIndex] ;
array[endIndex] = array[beginIndex] - array[endIndex] ;
array[beginIndex] = array[beginIndex] - array[endIndex] ;
}
}
else
{
cout << "out of array size";
}
}
void printResult()
{
for (int index = 0 ; index < swapCount; index++)
{
cout << swapArray[index] << "\\\\\\\\n";
}
cout << "end...\\\\\\\\n";
}
};
为减少不必要的查找,我们希望更早排除非最佳方案。有两个方面可以考虑:
1)根据目前的状态,预测至少需要翻转多少次才能排好序,如果预测值+目前已经翻转次数 > 目前最佳方案,则不用继续了。
2)考虑状态,如果当前状态之前出现过,则不用继续了。
对第一个问题,根据当前状态中的相连状态,可以预估一个最少翻转次数lowerBound。因为一次翻转最多使一个烙饼与大小和它相邻的烙饼排到一起,所以lowerBound的计算如下(实测过程中,对排列混乱的情况lowerBound的引入大大的提高效率):
lowerBound = 0;
for( index = 0; index < size - 1; index ++)
{
if(swapArray[index] - swapArray[index+1] !=1 && swapArray[index] - swapArray[index+1] != -1)
{
lowerBound++;
}
}
对第二问题,我们至少可以做到避免翻转会上一个状态。我们传入上次翻转位置,然后在本次中同一位置不翻转,直接退出。代码如下:
void search(int step,int lastIndex)
for(int index = 1; index < 10 ; index++)
{
if(index == lastIndex)
{
continue;
}
swap(index, cakeArray, 10);
tempSwapArray[step] = index;
search(step + 1,index);
swap(index, cakeArray, 10);
}
记录状态,我们容易想到的是将所有出现的状态缓存起来,然后搜素缓存中的状态和当前状态比较,如果状态中已经存在了,而且出现这个状态所用的翻转次数少于当前次数,直接退出。实际操作起来问题却很多,比如:
1) 怎样存储状态?
首先,存储数组是不合理的,不仅占用空间大,而且赋值操作多。需要转化一下。有几个转化思路
(1)将数组转化为字符串存储。
(2)将数组序列映射为整数。
2) 怎样搜索状态?
遍历搜索将大大的降低效率,因为搜索过程中比较太多。优化一下,可以用二分查找,这需要在缓存的时候,对状态排序。实际操作做还是进行可大量的比较,效率实际上降低了。转化一下,将数组序列映射的整数做为缓存数组的下标,在缓存中存bool值表示该位置对应的状态是否出现过。可是会消耗量的存储空间。
一番折腾,发现不是效率变低,就是存储空间太大(当然探索的过程中还是收获不少的)。所以缓存所有状态,好像不合理,那么我们退而求其次,只缓存当前翻转路径中的所有状态,也就是缓存从初始状态将到当前状态过程中的所以状态,然后搜索当前状态是否在缓存中出现过,这个是合理的,我们虽然在上面避免了马上回到上一个状态的过程,但是回到上两个、三个状态情况。
这里很适合用数据结构中的栈。进入下一个操作的时候,状态入栈,退出的时候出栈。
代码如下:
void search(int step,int lastIndex)
{
if(step + lowerBound() > swapCount || step > swapCount)
{
return;
}
if(findState())
{
return;
}
if(isSorted(10))
{
if (swapCount > step)
{
swapCount = step;
for (int index = 0 ; index < step ; index ++)
{
swapArray[index] = tempSwapArray[index];
}
}
return;
}
stateArray.push_back(toKey());
for(int index = 1; index < 10 ; index++)
{
if(index == lastIndex)
{
continue;
}
swap(index, cakeArray, 10);
tempSwapArray[step] = index;
search(step + 1,index);
swap(index, cakeArray, 10);
}
if(stateArray.size() > 0)
stateArray.pop_back();
}
搜索缓存
bool findState(){
for(int i = 0 ;i < stateArray.size(); i++)
{
if(toKey() == stateArray[i] )
{
return true;
}
}
return false;
}
状态数组转化为整数
int toKey(){
int result = cakeArray[0];
for(int i = 1 ; i < 10; i++)
{
result *= 10;
result += cakeArray[i];
}
return result;
}