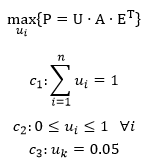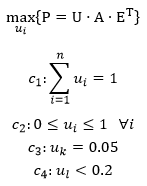1前言
对于对抗类游戏,无论是1v1还是5v5,FTG还是MOBA,只要存在多种策略供玩家选择,那么这些策略之间的“平衡性”就是一个老生常谈的问题,这里的策略可以是某个英雄(亚索)、某套组合(光猴、睡箭)、某种战术(人族TR)。如果某种策略过于强势,那么逐利的玩家就会倾向于只使用这种策略,从而导致整个游戏环境变得单一、缺乏变化和乐趣。因此游戏设计者需要对游戏中策略之间的平衡性进行评估,从而及时作出调整。
但是要评估游戏的平衡性并不简单,一方面对于大部分游戏而言,游戏中所包含策略的数量都很大,因为这样才有足够的游戏性和博弈空间,从而导致人工评估需要消耗极大的人力;另一方面,游戏中的策略也是动态变化的,随着开发者对游戏内容的修改(例如加强或者削弱某个英雄、新英雄新玩法的推出),或者仅仅是玩家开发出了一种新战术,都可能当前游戏的环境和平衡性产生冲击,因此评估结果还需要动态更新的,不能做成“一锤子买卖”。
本文以Alexander Jaffe在GDC2015上的一次分享“Metagame Balance For eSports&Fighting Games”(https://www.youtube.com/watch?reload=9&v=miu3ldl-nY4)为灵感,谈谈笔者利用“对战胜率/场次矩阵”进行游戏环境预测和平衡性评价的一点思路和效果。
该方法首先使用策略之间的对局胜率和游戏中不同策略的使用比例计算每种策略的“胜率期望”,然后以胜率期望为基础使用线性规划计算玩家胜率期望大于50%时每种策略的“可使用范围”,并以此作为评价策略平衡性的指标。
为了便于说明和理解,后文中使用“英雄”作为“策略”的代表,但请注意“策略”一词不仅仅包含英雄,而是“游戏对局战术思路”的合集。
2胜率期望计算
2.1对战胜率表与游戏环境
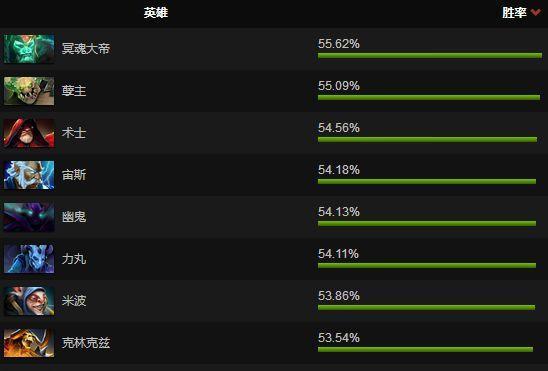
当谈到衡量英雄强弱的标准时,我们最容易想的是“英雄胜率”,在大量对局数据的基础上,胜率越高的英雄显然越厉害
Dotamax上的英雄胜率数据
但实际上英雄胜率是由2个部分组成的:英雄之间的强弱关系+游戏环境中不同英雄出现比例。例如对于2个胜率超过50%的英雄而言,可能1个是因为他打谁胜率都超过50%,另一个是因为目前游戏环境中某个英雄数量很多,而它正好是这个热门英雄的克星。
因此,要客观公正地评价英雄的强弱、平衡,需要同时考虑“英雄之间的强弱关系”和“游戏环境中不同英雄出现比例”,同样的高胜率英雄中,打谁胜率都超过50%的英雄显然更加的不平衡。上述2点可以分别用“对战胜率表(A)”“游戏环境(E)”进行描述。
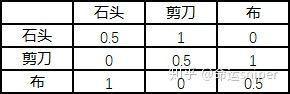
“对战胜率表(A)”是一个记录每个英雄两两之间的对局胜率的2维矩阵,每一行代表一个英雄在对阵其他英雄时的胜率,例如大家熟悉的石头剪刀布的对战胜率矩阵就是:
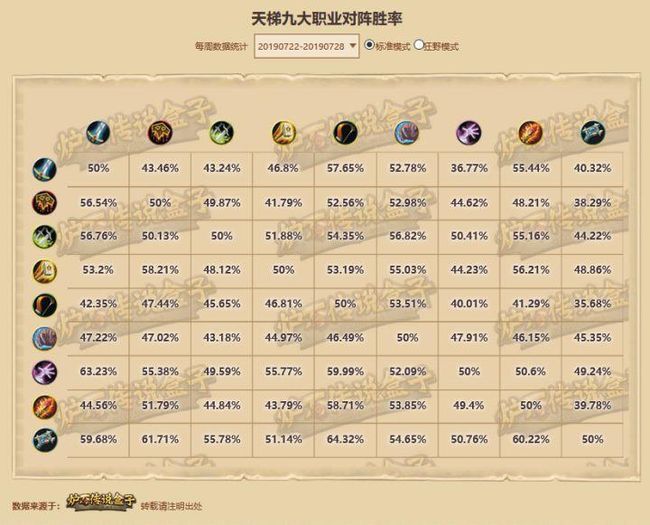
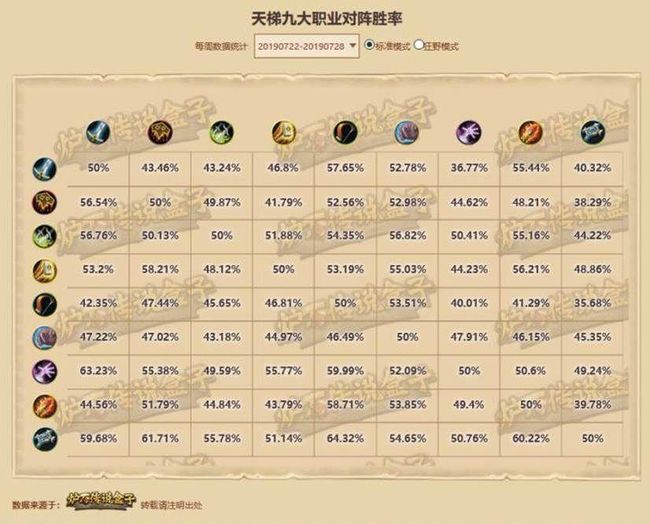
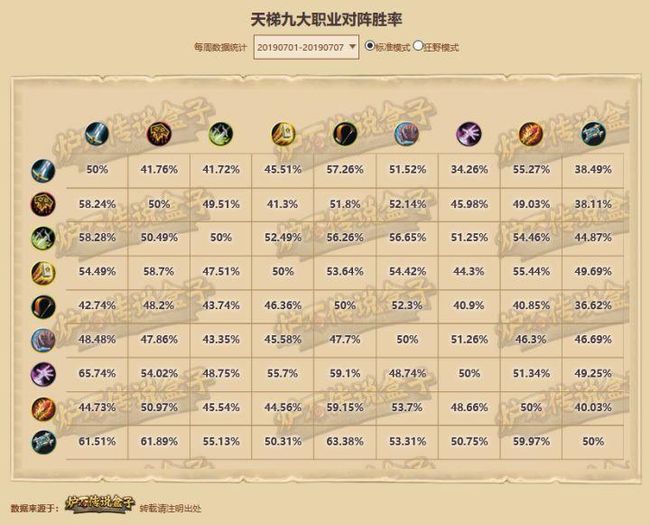
炉石传说中不同职业之间的对战胜率矩阵是:
数据来源:炉石传说盒子,http://lushi.163.com/bigdata/
“游戏环境(E)”虽然是一个抽象感念,但可以通过一个记录每个英雄出场次数在所有英雄出场次数中占比(也就是使用率)的1维矩阵来表示,例如:
代表目前游戏环境中有40%的人出石头,50%的人出剪刀和10%的人出布
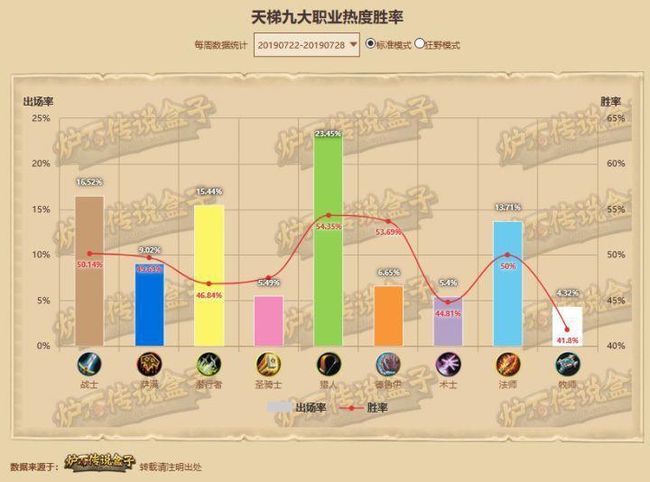
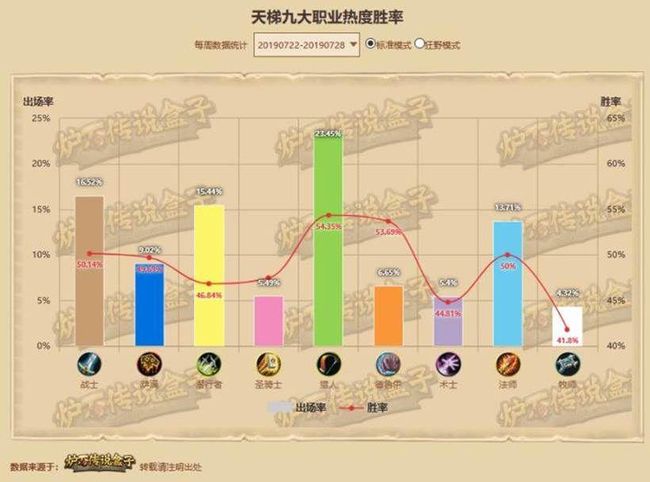
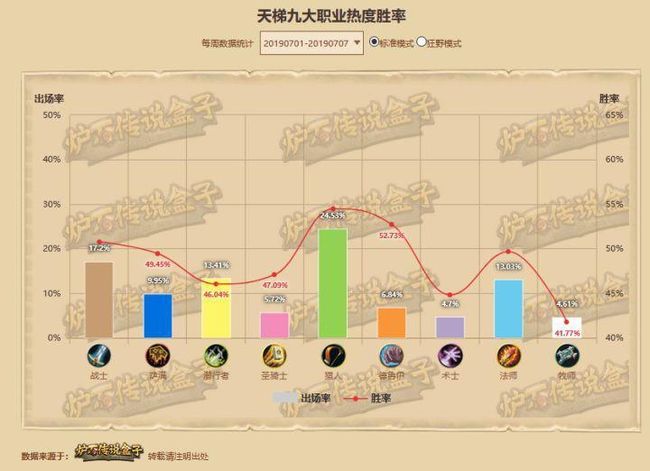
在比如炉石传说中不同职业的使用率为:
用1维矩阵表示即:
2.2玩家策略与胜率期望
在大部分游戏中,玩家在一次对局里只能使用一个英雄,甚至于在多次对局中,一些玩家也会只用1个或者少数几个英雄。
但是从统计角度来看,大量玩家的英雄选择、单个玩家在大量对局中的英雄选择是以一定的比例进行分布的,例如50%选A,30%选B,20%选C,我们可以用一个1维矩阵来表示,称为“玩家策略(U)”,例如:
表示一个玩家出剪刀和布的概率各为50%,绝对不出石头。
可以看出,玩家策略(U)和游戏环境(E)在结构上完全相同,因为本质上2者是相同的概念,只是玩家策略描述的是单个玩家在长时间内、大量玩家在短时间内对于英雄的选择偏好,而游戏环境则是描述大量玩家在长时间内对于英雄的选择偏好。如果所有玩家都追求高胜率且对游戏环境足够敏感,那么最终U和E将会趋于相等,意味着环境趋于稳定。
那么在对战胜率表(A)、游戏环境(E)、玩家策略(U)确定后,实际上我们可以根据这些数据计算出玩家的“胜率期望”P=U·A·ET(这里需要一些基础的矩阵运算知识),或者叫策略U的胜率期望。
以大家熟悉的石头剪刀布为例,如果当前环境E=[0.33,0.33,0.33],也就是其他玩家出剪刀石头布的概率都是三分之一,那么如果我只出剪刀U=[0,1,0],那么最终胜率会是0.5,
但如果当前环境是E=[0.5,0.5,0],也就是没有人出布,那么U=[1,0,0]的胜率就将会是0.25(从0.5的剪刀哪里吃平局的分)
所以我们可以看到,当玩家策略、策略与策略之间的对战胜负关系、游戏环境中的策略分布确定之后,那么玩家策略的胜率期望是可以计算出来的。如果一个策略的胜率期望高,那么说明这是一个强势策略,反之则是一个弱势策略。
进一步的,如果一个英雄总是出现在各种强势策略中,且一旦将这个英雄移除,强势策略就变得普通甚至弱势,那么说明这个英雄很强、用它就能赢;反之则说明这个英雄很弱,拉都拉不起来。这一计算过程充分利用了游戏中英雄之间的胜负关系和游戏环境里不同英雄的出场比例数据,比单纯使用英雄胜率评价英雄的强弱更加准确。
因此,通过计算不同玩家策略的胜率期望,可以更加准确地发现游戏中那些明显过强、过弱的英雄,进而评价游戏的平衡性。
3游戏平衡性评价
3.1平衡性的定义
在使用胜率期望进行游戏平衡性评价之前,我们首先要弄清一个问题:什么样的游戏环境是健康、平衡的?
可能对于不同的设计师来说这个问题有不同的答案,当然哪个对哪个错也没有定论,但本文提出一个观点——玩家在游戏中达到50%胜率所能使用的英雄越多,那么游戏环境就越平衡、健康。
对玩家来说,如果用一个英雄自己输多胜少,那么这个英雄本质上是弱势的,有可能这个英雄很好玩,赢一把爽一天,但对于游戏环境来说这个英雄很弱。不过好玩和能赢哪一个更重要又是另一个问题了,此处按下不表。
如果将“玩家在游戏中达到50%胜率所能使用的英雄数量”作为评价游戏平衡性的指标,那么真的就仅仅是“胜率超过50%的英雄越多就越好越平衡”这么简单?显然也不是,毕竟游戏里不可能大部分英雄胜率都超过50%。这里需要将玩家多次游戏中不同英雄的使用比例纳入考虑的范围,用到第二节里提到的“玩家策略”这一概念。
对于一个英雄A,玩家如果只用A,可能胜率不足50%,但是十次游戏里用8次A,其他2次用其他版本强势英雄,最后整体胜率超过50%,那么整体体验也是良好的。
对于一个英雄B,如果玩家在十次游戏中只能用一次,如果用了2次,即使其他8次都用胜率最高的英雄最后总体胜率期望也不足50%,那么英雄B显然太弱了,属于弟弟角色。
对于一个英雄C,如果玩家十次游戏中得用他至少5次,否则如果只用4次,剩下6次无论怎么选择英雄,最后胜率都不足50%,那么英雄C显然太强了,玩家不玩C就寸步难行。
为此,我们需要以每个英雄为粒度,计算“玩家若想整体胜率超过50%,该英雄的出场率范围是多少”,换言之,如果在玩家策略中该英雄的出场率低于或高于这个范围,那么玩家的胜率期望将会低于50%。如果这个出场率范围合理,说明这个英雄的强度合理;如果强度合理的英雄数量足够多,那么说明整个游戏环境是平衡和健康的。
3.2出场率范围计算
对于2.2节中提到的P=U·A·ET,在英雄对战胜率表A和游戏环境E已知且不变的情况下,如果没有其他约束条件,利用简单的矩阵运算就可以求出在此条件下最佳的玩家策略U,使得P最大。
但在实际游戏中,除了U、A、E这3个矩阵的规范性外(例如单英雄使用率在0到1之间),还可能有一些其他的限制条件,例如某个英雄由于其上手难度很高因此使用率存在某个上限,或者某个英雄由于其人气很高因此使用率存在一个下限等等。
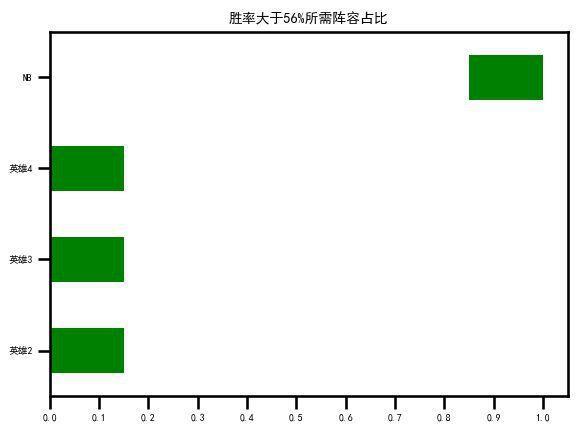
为能够兼容对这种复杂条件下的计算,这里使用了线性规划的方式,即将U=[u1,u2,…,un]作为参数,在一定的约束条件C={c1,c2,…,cm}的约束下,求解P=U·A·ET的最大值以及对应的U,例如:
其中c1和c2是对U规范性的约束(英雄使用率之和为1,单个英雄使用率在0到1之间),c3:uk=0.05代表正在求解玩家以5%的使用率使用第k个英雄时的最高胜率期望。
当按0.05、0.1、0.15、0.2……0.95、1的形式不断变化uk的取值时,就可以算出对于第k个英雄而言,在不同使用率下的最高胜率期望,得到如下所示的一系列结果
![]()
其中,[使用率0.35,胜率期望48.42]的含义是,如果要求玩家在自己的策略中以35%的比例使用该英雄(不能多也不能少),那么这个玩家最多只能找到一个胜率期望是48.42%的策略,也就意味着玩家找不到任何一个策略能够让自己的胜率期望超过50%。
然后我们将其中胜率期望大于50%的部分标记为绿色,表示在对应的使用率下,能够找到一个玩家策略使得玩家的胜率期望大于50%。
![]()
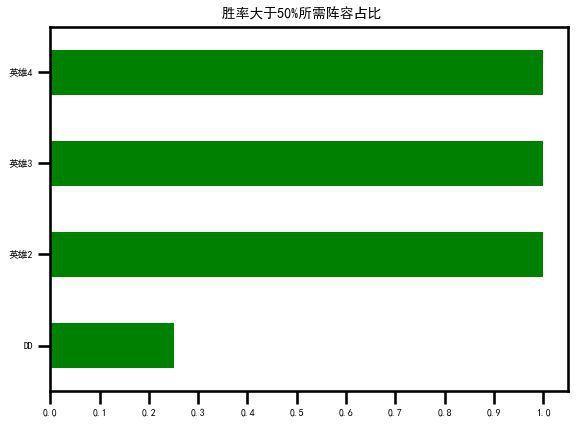
更换求目标英雄k,重复上述求解过程,将会得到一系列[使用率,胜率期望]的计算结果。我们以使用率为横坐标,英雄为纵坐标,将每个英雄标绿的部分画在一张图上,并按绿条的长度进行排序,有如下结果:
可以看到,英雄8和4很厉害,即使玩家只用这一个英雄(使用率为100%),也能有超过50%的胜率,而英雄1、10、9则很弟弟,最多只能用15%到20%,否则就拿不到50%胜率。
下面我们以几个典型对局例子看看这套评价方法的结果如何,其中游戏环境假定为各种策略的使用比例相同。
首先是剪刀石头布:
说明每种策略都可以全用或不用(当然前提是游戏环境中剪刀石头布的出现概率都是三分之一)
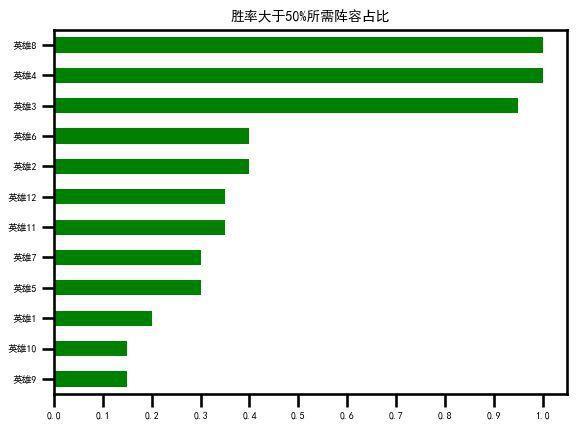
第二种是存在过强的英雄
对于那个过强的英雄,如果玩家想要获得50%以上的胜率,至少得拿出四分之一的比例来使用它,而对于其他3个一般的英雄,使用比例则不能高于四分之三。
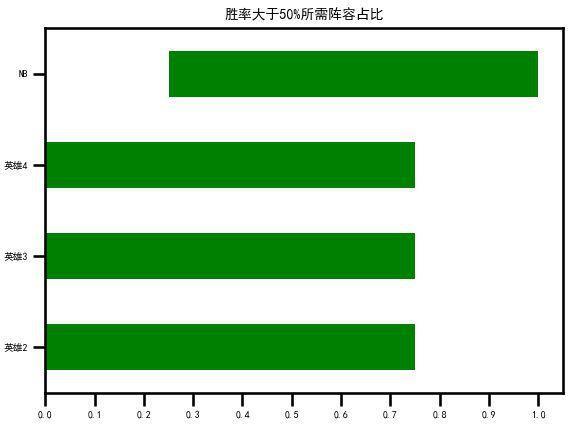
如果我们把“标绿”的阈值提高,把目标提升到超过56%胜率,甚至可以出现如下结果:
只用NB英雄的话,可以获得超过56%的胜率
第三种,过弱的英雄
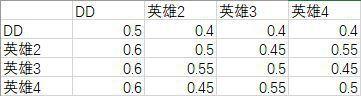
别的英雄都可以随便用,但唯独这个DD英雄的使用率不能超过四分之一,否则胜率就达不到50%
最后我们以前面给出的炉石传说的对局胜率和游戏环境为例进行一下计算
注意这里的胜率矩阵是纵向排布的,即第一行是[各职业对阵战士]的胜率,特别注意的是,所有职业对阵德鲁伊的胜率均小于50%
数据来源:炉石传说盒子,http://lushi.163.com/bigdata/1
3.3有约束条件下的平衡性计算
3.2节讨论了当对玩家策略不做任何约束的情况下的平衡性计算,但在实际游戏中,因为玩家喜好、英雄池的不同,是存在一些潜在约束条件的。
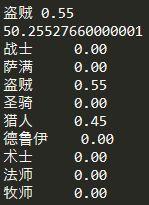
以3.2节最后的炉石传说的计算结果为例,在胜率大于50%的求解结果中,看上去圣骑、盗贼在使用率超过50%的情况下,也能够获得超过50%的胜率,但是如果我们将求解的“最佳策略”输出出来就会发现,在盗贼使用占比55%的情况下,剩下45%必须全部用猎人才能获得50.26%的胜率。
如果一个玩家不喜欢玩猎人,或者目前手里的牌构筑不出环境中主流猎人的卡组,那么这个玩家55%使用盗贼的情况下就“有可能”拿不到50%的胜率了。
因此,3.2节的求解过程中,如果有一定的先验知识,那么可以加入一些额外的约束条件来使得整个求解结果更加接近于真实结果
这里的c4:ul<0.2就是额外的约束条件,要求第l个英雄的使用率不能超过0.2。
加入一个约束条件对于求解问题本身并没有难度,只是要注意2点
1是约束条件C={c1,c2,…,cm}本身需要是自洽的,不能既要求u1>0.6,u2>0.6,还要求u1+u2≤1
2是当求解到k=l的相关情况时(uk=0.05、0.10…),在代码中要做好处理,确定以谁为标准,是uk=0.05还是ul<0.2
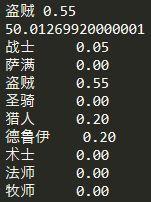
我们将“猎人、德鲁伊的使用率≤20%”作为条件加入到前面的炉石求解过程中,得到结果:
可知,限制了猎人、德鲁伊的使用率后,玩家在55%使用盗贼的情况下已经只有50.01%的胜率了
3.4问题点讨论
3.4.1数据缺失问题
如果游戏的玩家数量不够多,或游戏版本更新较快,会导致同一个游戏版本中难以获得足够多数量的对局覆盖所有英雄之间的对抗情况,最终导致“对战胜率矩阵”中存在空缺值。
对于这种情况,有2种解决方案
方案1是人为根据经验、其他相似英雄的对局胜率估算一个胜率填补空缺值
方案2是在求解计算时,“不让没有对局胜率的2个英雄碰面”,即将本应该属于他们2人的对局分配给其他有对局胜率的英雄
例如本来环境中石头、剪刀、布的分布是0.4、0.4、0.2,但现在布和石头的对局胜率缺失了,那么在计算到0.2*[石头VS布]时,就用0.1*[石头VS石头]+0.1*[石头VS剪刀]来代替
图中函数getWinRateNow是用来计算玩家策略(myArray)对抗游戏环境(enemyArray)时的胜率期望,对于每一个heroMe,55-57行用noRate统计了其存在空缺值(对局胜率小于0)的场次比例,并在61行在计算有对局胜率的场次时除以(1-noRate),从而实现将缺少数据的场次按比例分配给有数据对局。
但是该方案也仅仅适用于空缺值较少的情况,如果对于某个冷门英雄缺失了很多对局胜率数据,那么这种将空缺场次分给非空缺场次的做法会带来比较明显的偏差,一个极端的例子是如果这个英雄只和一个英雄有对局胜率,胜率是55%,那么最终结果将会是这个英雄对阵每个英雄的胜率都是55%,这显然是不合理的。
3.4.2“策略”的粒度问题
正如第1节所说,“策略”是讨论游戏平衡性的单位,但是具体到实施中,对游戏中的“策略”进行归类时粒度的粗细却不好把控,可以将大致相似的策略都归为一种,也可以将但凡有一丁点不同的策略都视为不同的。
以WAR3为例,我们可以简单地将兽、人、暗夜、亡灵作为4个策略,也可以将同一个种族的不同套路例如暗夜-乱矿流、暗夜-吹风流视为不同的策略,还可以将同一个种族、同一个套路但首发不同英雄视为不同的策略,甚至还可以继续细分。那么到底细分到哪个粒度可以认为是“够了”,或者说2个策略相似到何种地步就可以认为是同一个策略?
这个问题笔者认为只能说因游戏而已。
有的游戏很容易给出2个策略之间数值上的相似/差异程度,例如炉石传说的2个套牌之间可以用不同卡牌的张数来体现差异,从而很容易归类出相似套路的卡组;而有的游戏则不好判断2个策略到底差别有多大,例如MOBA里一个五人队伍把辅助A换成辅助B,有可能最终队伍的战术玩法完全没有区别,也有可能完全不同。
另一方面,有的游戏DAU高、对局数据量很大,即使将策略划分得很细致,搞出几十几百个策略,策略之间的两两对局胜率也不会出现空缺值,而有的游戏DAU低、对局数据不足,稍微把策略划分细致一点就出现大量空缺值,自然也就让平衡性的计算无从下手了。
4游戏环境预测
4.1简单粗暴的环境预测
从第三节中可以看出,游戏环境与游戏平衡性计算关系密切,一方面计算P=U·A·ET时游戏环境(E)是必不可少的要素,另一方面在存在数据空缺值时也可以通过游戏环境进行一定程度地弥补。
虽然当前的游戏环境是很容易通过数据统计的方式得到的,但游戏环境是动态变化的,如果仅仅利用“当前游戏环境”来评估游戏平衡性,那么评估结果仅仅只是“当前环境”的评价,在指导后续游戏调整上还存在不足。如果能够预测在不加入其他干预的情况下游戏环境会如何变化,对于游戏设计者来说将更加能够把控游戏环境与玩家体验。
但是对游戏环境的预测是一门很复杂的学问,涉及很多方面。本文提出一种较为简单粗暴的环境预测方法,该方法假设玩家都是追逐胜率的,会根据游戏环境调整自己的策略选择胜率最高的策略,而这一行为又会影响游戏环境,从而形成一个循环,最终达到稳定,即全部玩家都选择同样/相似的策略,大家的胜率都是50%。
具体而言,整个预测过程是一个迭代循环:
1、根据P=U0·A·E0T求解对于当前游戏环境E0和对战胜率A而言的最佳玩家策略U0
2、根据U0将游戏环境E0按一定演变系数x向U0靠近,模拟玩家因为追逐胜率选择版本强势英雄的过程,得到新的环境E1,即
3、返回第一步,用E1求解新的最佳玩家策略U1,反复迭代一定次数,或直至En和En+1的向量距离小于特定参数,代表游戏环境趋于稳定
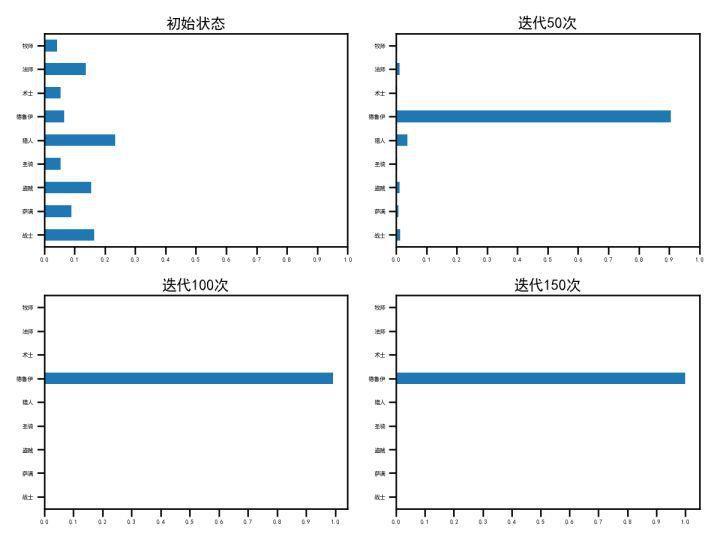
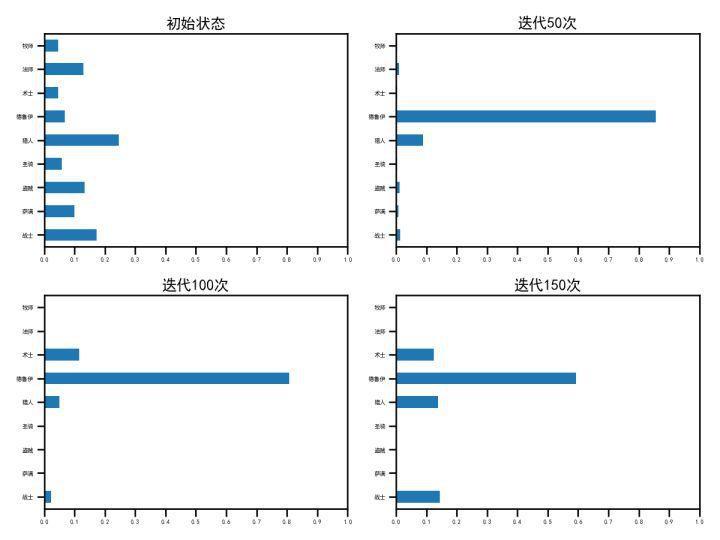
以前面用到的炉石传说的环境为例进行预测,演变系数x取0.05,得到如下结果:
由于德鲁伊打谁都超过50%的胜率,导致最后大家都用德鲁伊了
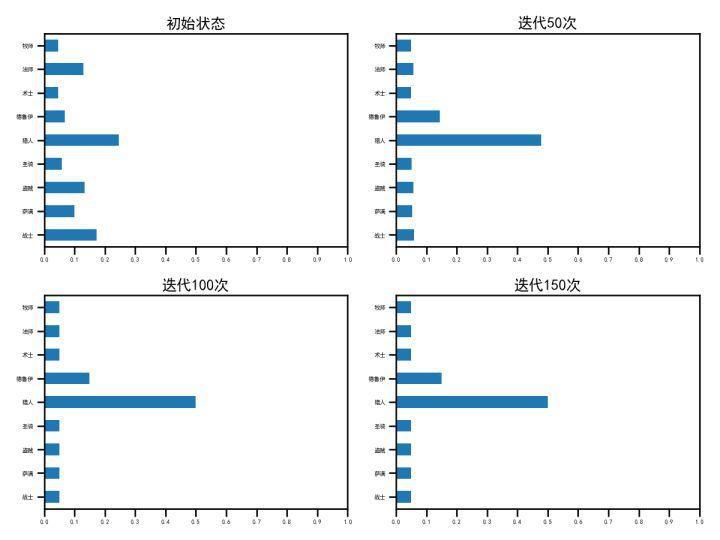
由于这样的数据和结果实在不具有分析和验证的能力,我们再往前选择7月1日-7月7日的数据
得到如下结果
最初由于德鲁伊的强势,德鲁伊迅速崛起,但随着德鲁伊数量越来越多,唯一能打德鲁伊的术士变多,从而带动了特别能打术士的猎人(59%胜率)和战士(65%胜率)
4.2附带限制条件的环境预测
出于和第三节提到的类似的原因,在实际游戏中可能存在一些先验的约束条件,例如游戏中最多只有15%的人拥有一个牛逼英雄,或者某个角色最少也有5%的死忠粉。
因此和3.3节一样,需要将上述条件带入到求解最佳玩家策略U的线性规划中,例如我们假设炉石中9个职业均至少有5%的使用率,最高不超过50%,那么最终的环境预测结果是
虽然德鲁伊除了对阵术士外均是优势对局,但是猎人在平均胜率上更高,因此从其他职业身上“吃分”的效率更高。
4.3存在问题的地方
4.3.1演变系数x的确定
环境预测的每次迭代计算中,当前环境向当前最优解靠近的速度是由演变系数x确定的,4.1节所提到的方案中x是固定值,这并不合理,因为游戏环境的变化速度由很多原因决定,并不是固定的。因此这也导致预测结果的指导意义不足,我们无法知道“迭代50次”所展示的结果大概会在多少天后出现。
4.3.2演变系数x的生效方式
对于求解“当前环境下的最佳玩家策略”这一步而言,通过简单的矩阵运算知识可以证明最终求解结果将会是某个“最优英雄”的使用率为100%,其他英雄使用率为0%。因此4.1节所提到的“当前环境向当前最优解的靠近”在本质上是让环境中使用非最优英雄的玩家减少一定比例转去玩最优英雄。
但实际上,使用不同非最优英雄的玩家并不会同等比例地转去玩最优英雄。首先自身胜率超过50%的玩家可能并不会换英雄,其次自身胜率低于50%的玩家可能换去转去玩胜率超过50%但并不最优的英雄
4.3.3对战胜率表的变化
前面的整个预测过程中,对战胜率矩阵是保持不变的,但实际情况下,随着游戏环境的变化,胜率矩阵大概率是也会变化的,例如开发出针对当前热门英雄的打法,或者大量玩家在“打不过就加入后”由于自身对强势英雄并不熟悉,导致强势英雄的胜率降低等等。
结语
本文的起因是对Alexander Jaffe在GDC2015上分享进行复现和评估。在复现中发现其方法存在一定的弊端,例如使用“最低胜率”而非“胜率期望”作为评估一个玩家策略优劣的标准、未考虑游戏中不同策略的使用比例等等。
于是在充分拆解了Alexander Jaffe所提方法的计算流程和逻辑后,提出了本文中的游戏平衡性计算与评价方法,且由于需要用到“游戏环境”作为输入数据,简单实现了一种游戏环境的演变预测方法,最终觉得可以进行一下分享和讨论。
从实践效果上看,2个方法所得到的结果存在一定的指导意义,尤其是游戏平衡性评价方法输出的结果比单看胜率、出场率要更加客观。但2个方法也有比较明显的问题和弊端,存在一些“拍大腿”定下的参数,例如以50%胜率作为划分标准和4.3节提到的问题。
后续准备结合项目组已有和未来的数据调整一些评价、预测的细节,并调研看看目前业界在这方面有没有什么好方法。
相关代码见:https://github.com/lwt1231234/MetaGame
作者:命运sniper
专栏地址:https://zhuanlan.zhihu.com/p/76479087