指数衰减的学习率
运行环境
python3.6.7、tensorflow1.4.0
测试思路
给定1000组数据,每组数据输入为一个值x,输出为一个值y,y由x线性变换而来,映射关系为y = 0.6x + 0.4,为模拟真实数据,在生成y的过程中加入了随机噪音。用这些数据用于训练,w和b初始化为0,采用梯度下降算法,损失函数取均方误差,通过设置不同的学习率来观察学习率对最终迭代结果的影响,并在最后采用指数衰减的学习率进行启发式的学习。
源代码
# -*- coding: UTF-8 -*-
#Author:Yinli
import tensorflow as tf
import numpy as np
from numpy.random import RandomState
import os
#设置只显示warning和error
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
#设置学习速率、batch数量和迭代次数
#初始学习率为1.0,每训练10次后学习率乘以0.96
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(1.0, global_step, 10, 0.96, staircase=True)
#LEARNING_RATE = 1.0
#LEARNING_RATE = 0.01
BATCH_SIZE = 10
STEPS = 1000
#为x和y_设置placeholder
#x是输入,每组数据1个属性
#y_是正确输出,每组数据一个值
x = tf.placeholder(tf.float32, shape=(None, 1), name='x')
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y_')
#初始化w和b为0
w = tf.Variable(tf.constant(0, dtype=tf.float32))
b = tf.Variable(tf.constant(0, dtype=tf.float32))
#规定映射函数,y=w*x+b
y = x*w + b
#规定损失函数为正确值和预测值的均方误差
loss = tf.reduce_mean(tf.square(y_-y))
#定义训练步骤,采用梯度下降
train_step = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(loss,global_step)
#随机生成1000*1的输入数据,即1000组输入数据
rdm = RandomState(1)
dataset_size = 1000
X = rdm.rand(dataset_size, 1)
#用X生成Y,其中给定w=0.6,b=0.4,再加入随机值模拟噪音
Y = [[(0.6*x+0.4+rdm.rand()/10.0-0.05)] for x in X]
with tf.Session() as sess:
#初始化数据
init_op = tf.global_variables_initializer()
sess.run(init_op)
#迭代
for i in range(STEPS):
#每次选择一批数据
start = (i*BATCH_SIZE) % dataset_size
end = min(start + BATCH_SIZE, dataset_size)
#对这批数据采用梯度下降的算法进行更新
sess.run(train_step, feed_dict={x:X[start:end], y_:np.reshape(Y,(1000,1))[start:end]})
#每100次迭代打印查看当前的w和b
if i%100 == 0:
print("————第%d次迭代————"% i)
print("w的值为", sess.run(w),end=" ")
print("b的值为", sess.run(b))
运行结果
当学习率为0.01时
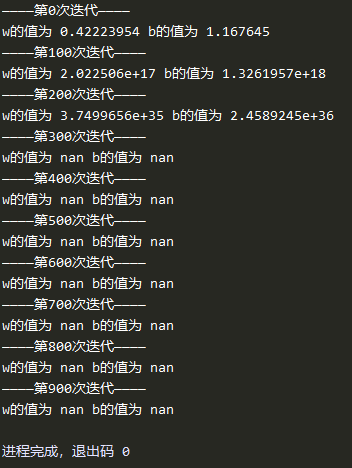
当学习率为1时
使用指数衰减学习率
结果分析
从三种学习率中可以看出来,当学习率取0.01时,经过1000次迭代后还没有收敛到正确的w和b附近,说明学习率小了收敛速度慢。当学习率取1时,梯度下降的步伐太大导致震荡得到无穷大的结果,而当采用了指数衰减的学习率,初始学习率为1,每迭代10次学习率乘以0.96,这样可以在保证速度的同时使得学习步伐在后期不会太快,最终在400次左右就收敛到了正确值附近。
滑动平均模型
运行环境
python3.6.7、tensorflow1.4.0
滑动平均模型介绍
除了指数衰减策略之外,tensorflow还提供了滑动平均模型来实现逐渐变小的学习率,滑动平均模型需要提供一个decay值,还可以提供step用来记录当前迭代的次数,滑动平均后的变量记为shadow_variable,有如下关系:
shadow_variable = shadow_variable × decay + (1 - decay) × variable
其中decay值在地带前期取(1+step)/(10+step),在后期取给定的decay值,取两者的最小值,这样就可以实现随着迭代次数的增加,滑动平均变量的变化趋于稳定,而在迭代前期滑动平均变量变化比较大,滑动平均模型实现见下
源代码
# -*- coding: UTF-8 -*-
#Author:Yinli
import tensorflow as tf
#初始化v1为0,v1是用来计算滑动平均的值
v1 = tf.Variable(0,dtype=tf.float32)
#step是当前迭代的次数,将trainable设置为False是为了改变step观察结果
step = tf.Variable(0,trainable=False)
#ema是一个滑动平均的类,设定decay值为0.98
#传入step是为了在训练前期更新得更快
#训练前期step小,decay值取的就是(1+step)/(10+step)
ema = tf.train.ExponentialMovingAverage(0.98, step)
#定义滑动平均操作
maintain_op = ema.apply([v1])
with tf.Session() as sess:
#初始化参数
init_op = tf.global_variables_initializer()
sess.run(init_op)
#观察初始的v1和滑动平均值
print(sess.run([v1, ema.average(v1)]))
#将v1初始化为5,进行滑动平均,打印v1和滑动平均后的v1
#此时step为0,decay取0.1,滑动平均后为4.5
sess.run(tf.assign(v1, 5))
sess.run(maintain_op)
print(sess.run([v1,ema.average(v1)]))
#将步数设置为1000,v1设置为10
sess.run(tf.assign(step,1000))
#sess.run(tf.assign(v1,10))
#进行滑动平均操作并打印结果
#此时decay取0.98,滑动平均后为0.98*4.5+0.02*5=4.51
sess.run(maintain_op)
print(sess.run([v1, ema.average(v1)]))
#再次进行滑动平均并打印结果
#此时decay取0.98,滑动平均后为0.98*4.51+0.02*5=4.5198
sess.run(maintain_op)
print(sess.run([v1, ema.average(v1)]))