这篇文章起于我与男票的一个讨论。有一天在杂志上一眼撇到Monte Carlo这个词,就随口说了一句有一种Monte Carlo Simulation是一种基础的数据模拟方法,激发了他的好奇心。 【悔不该当初地捂脸】
所以我们俩就开始了对蒙特卡罗模拟方法的讨论。
Monte Carlo:
蒙特卡罗方法(英语:Monte Carlo method),也称统计模拟方法,是1940年代中期由于科学技术的发展和电子计算机的发明,而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
Monte Carlo一般的应用,就是一个输出结果,有好几个带有不确定性的输入数值,并且每个输入都有不同概率分布的时候,我们可以用蒙特卡洛模拟方法来产生成千上万的随机数进行模拟,最后看模拟出来结果的分布,就可以了解我的输出
实现的工具有,最简单的如Excel,更加复杂或者需要比较大的随机数组的可以用R或者其他的数据工具。
就这样, 我讲了半天,口干舌燥,仍是没让他一个天天琢磨机器学习的人听明白我说的是啥,另外他所不解的一段,为什么不能直接通过推导公式的方法算出输出的平均值和标准差。 这个时候,真心觉得。。。无论多么高大上的术语,在一个对某方面一无所知的人面前,是多么的苍白无力啊。。。。
反倒是他“语重心长”地跟我说,
”费曼曾说过,如果我们无法把一个理论简化至大学一年级的程度,我们就不算真正理解这个理论。“
【费曼式意味深长笑。。。】
啊 我摔!
非常巧的一件事情是,不到一个星期,刚巧在吴军老师的专栏里提到这个理论。短短几行,简介明了。 哎,所以我的解释一定是哪里出了问题。
如果上天再给我一次机会的话。。。
不管了,我们推倒重来。
蒙特卡洛模拟可以用来解决一些有多个影响因素,且复杂的概率分布时候,用于在复杂系统中进行结果模拟。
举个简单的例子:我计划明年开一个炸鸡店。
对于可能影响我收益的因素,我作了以下调研:
1. 店铺的租金。根据调研,我发现我想要开店地域的租金价格分布,平均价格是两万五,呈正态分布。 (简单的说,就是说大多数的店铺租金价格为两万五,租到更贵或者更便宜的店铺的可能性都在逐渐减小,极端价格的可能性低)
2. 通过分析与我类似地点的同类商家,我发现我的炸鸡日销量最高可能为2万个,最低销量为一万个,其他点销量的概率为线性分布。
3. 我的店员人工成本按照市场价格,人工成本的平均数为一万块钱一个月,呈正态分布。
4. 通过行业人数,我了解到明年炸鸡成本有涨价的可能。保持现价一块钱一个的可能性为40%,涨为1块二一个的可能性为60%。 (这个数是我胡诌的。。。)
5. 其他的浮动成本以及补贴,如水电煤气费,当地某大哥可能会跟我要的保护费,正在申请但是只有30%可能性能拿到的中小企业补贴费等等等等。。。
请问,在这些条件以及相应的不确定性下,我明年开炸鸡店是会赔还是赚?
这样复杂的问题,有很多变量的情况下,会发现用简单的数学公式
利润=炸鸡销售量*(销售单价-炸鸡批发价)-人工成本-租金成本-其他成本
已经很难预估到可能出现的结果了。
-那怎么办?
-答案: 蒙特卡洛模拟
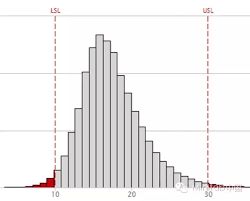
通过随机生出一万种不同的排列组合,相当于模拟一万次开店的场景,算出来每次的收益。这么大的数据组可以帮我把最好的结果,最坏结果,一般般的结果都生成。通过这个数据组,我就可以画出一个概率分布图,了解到每个可能出现的结果所对应的可能性。
比如说上面这样的。
通过这种图,我就可以了解到,我明年开炸鸡店,年盈利100万的可能性为20%,盈利50万的可能性为50%,赔钱的可能性为30%。 这样我就能够估计出我作这个决定的风险以及可能的收益,来帮助我作出对的决策。
并且我产生的随机数组数量越大,得出的概率分布就会越接近真实发生的可能性。(当然同时的前提是我的输入分布也给的很准确)。
此外,这个模型还可以辅助我来作What-if analysis (直译为:如果情况的分析)。比如说我通过Monte Carlo 模拟之后发现,当房租成本上限为两万块钱块的时候(举例,数是胡诌的),我的利润就有98%的可能性是正值,2%为负。那么作为一个经营者,我就知道,要想稳赚不赔,必须找一个租金成本在两万块钱以下的店铺。
所以蒙特卡洛在数据分析中是一个非常实用的模型。
最后分享一个电视剧中让我拍脑瓜瞬间”Aha “的片段。英剧《黑镜》通过架空演绎,设想各种黑科技科技给人们生活带来的影响。其中有一集叫作Hang the DJ。讲述的是,在未来社会,人们通过App来计算两个人的匹配度。
实现的方法就是将双方性格的信息输入到系统里,在系统中生成两个与原主性格等一切条件都符合的两个人物,在一个好似Matrix的系统里 (《黑客帝国》里的系统名称),通过模拟1000次恋爱场景并设置考验,来测试两个人的契合度。 剧中的男女主人公的虚拟小人为了在一起, 1000次中有998次为真爱选择了私奔,只有两次没有。最终系统判定两个在现实生活中有99.8%的可能性有情人终成眷属。
这就是蒙特卡洛模拟方法的一个典型应用。
虽然统计学和数据不等同于生活,复杂多变的生活也很难用冷冰冰的模型来,我们更没法保证我们一定不会在有生之年活成那0.2%的结果。 Monte Carlo之美就在于,上千万次的模拟,让人们在接近于零的试错成本下,了解一个选择风险或者得到某种结果的可能性。在现实生活中,在有效的时间和资源里,我们很难通过尝试一两次就准确地估计出结果。就好比黑镜中男女主角需要跟每次都花几个月去跟不同的人谈恋爱直到遇到对的为止,同样我在开炸鸡店点之前就能对我所面临风险进行评估。
生活比模型更加精彩。同样,期待在未来,蒙特卡罗模型在生活中能够有更多的应用,辅助人们作出决策。
Tiffany,一个没事爱琢磨的理科生。喜欢就点个赞吧。