好萌的讲解
以下为部分摘取的一些定义
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集 U 和 V ,使得每一条边都分别连接U 、 V 中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。
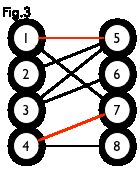
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
完备匹配:在一个二分图中找到u->v的一个匹配方案,使得U中所有点出现在该匹配中。
匈牙利算法是用来求解二分无权图的最大匹配算法
HDU - 2063 过山车
题意:
二分图无权图的最大匹配
题解:
- 邻接矩阵的匈牙利算法
#include
#include
#include
#include
using namespace std;
const int MAXN=510;
int graph[MAXN][MAXN];
int flower[MAXN];
int used[MAXN];
int n,m;
bool DFS(int x)
{
int i;
for(i=1;i<=m;i++)
{
if(graph[x][i]&&!used[i])
{
used[i]=1;
if((flower[i]==0)||(DFS(flower[i])))
{
flower[i]=x;
return true;
}
}
}
return false;
}
int main()
{
int k,a,b;
while(scanf("%d",&k)!=EOF,k)
{
scanf("%d%d",&n,&m);
memset(graph,0,sizeof(graph));
memset(flower,0,sizeof(flower));
set girl;
for(int i=1;i<=k;i++)
{
scanf("%d%d",&a,&b);
graph[a][b]=1;
girl.insert(a);
}
int sum=0;
for(set::iterator it=girl.begin();it!=girl.end();it++)
{
memset(used,0,sizeof(used));
if(DFS(*it)) sum++;
}
printf("%d\n",sum);
}
return 0;
}
- 邻接表的匈牙利算法
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=510;
vector graph[MAXN];
int flower[MAXN];
int used[MAXN];
int n,m;
bool DFS(int x)
{
for(int i=0;i girl;
for(int i=1;i<=k;i++)
{
scanf("%d%d",&a,&b);
graph[a].push_back(b);
girl.insert(a);
}
int sum=0;
for(set::iterator it=girl.begin();it!=girl.end();it++)
{
memset(used,0,sizeof(used));
if(DFS(*it)) sum++;
}
printf("%d\n",sum);
}
return 0;
}
- 前向星的匈牙利算法
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=510;
const int MAXEDGE=1010;
struct Node
{
int to,next;
};
Node Edge[MAXEDGE];
int head[MAXN];
int cnt;
void addEdge(int u,int v)
{
Edge[cnt].to=v;
Edge[cnt].next=head[u];
head[u]=cnt++;
}
int flower[MAXN];
int used[MAXN];
int n,m;
bool DFS(int x)
{
for(int i=head[x];i!=-1;i=Edge[i].next)
{
if(!used[Edge[i].to])
{
used[Edge[i].to]=1;
if((flower[Edge[i].to]==0)||DFS(flower[Edge[i].to]))
{
flower[Edge[i].to]=x;
return true;
}
}
}
return false;
}
int main()
{
int k,a,b;
while(scanf("%d",&k)!=EOF,k)
{
scanf("%d%d",&n,&m);
memset(flower,0,sizeof(flower));
memset(head,-1,sizeof(head));
cnt=0;
set girl;
for(int i=1;i<=k;i++)
{
scanf("%d%d",&a,&b);
addEdge(a,b);
girl.insert(a);
}
int sum=0;
for(set::iterator it=girl.begin();it!=girl.end();it++)
{
memset(used,0,sizeof(used));
if(DFS(*it)) sum++;
}
printf("%d\n",sum);
}
return 0;
}
其实二分匹配也可以用最大流来做的
建一个超级源点,连向一边所有的点 容量为1;
另外一边点都连向汇点 容量为1;
二分图的边容量也为1
然后跑一遍最大流即可
#include
#include
#include
#include
using namespace std;
const int MAXN=1010;
const int MAXE=5010;
const int INF=0x3f3f3f3f;
int head[MAXN],cnt;
struct Node
{
int to,next,val;
Node(){}
Node(int to,int next,int val):to(to),next(next),val(val){}
};
Node edge[MAXE];
void addEdge(int u,int v,int val)
{
edge[cnt]=Node(v,head[u],val);
head[u]=cnt++;
edge[cnt]=Node(u,head[v],0);
head[v]=cnt++;
}
int step[MAXN];
bool BFS(int st,int ed)
{
queue que;
que.push(st);
memset(step,-1,sizeof(step));
step[st]=0;
int u,v;
while(!que.empty())
{
u=que.front();
que.pop();
for(int i=head[u];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(step[v]==-1&&edge[i].val>0)
{
step[v]=step[u]+1;
que.push(v);
if(v==ed) return true;
}
}
}
return false;
}
int DFS(int st,int ed,int flow)
{
if(st==ed||flow==0) return flow;
int v,curr=0;
for(int i=head[st];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(step[v]==step[st]+1&&edge[i].val>0)
{
int d=DFS(v,ed,min(flow,edge[i].val));
if(d>0)
{
edge[i].val-=d;
edge[i^1].val+=d;
curr+=d;
flow-=d;
if(flow==0) break;
}
}
}
if(curr==0) step[st]=INF;
return curr;
}
int Dinic(int st,int ed)
{
int flow=0;
while(BFS(st,ed))
{
flow+=DFS(st,ed,INF);
}
return flow;
}
int main()
{
int k,m,n,a,b,st,ed;
while(scanf("%d",&k)!=EOF,k)
{
scanf("%d%d",&m,&n);
memset(head,-1,sizeof(head));
cnt=st=0;
ed=m+n+1;
for(int i=1;i<=m;i++)
{
addEdge(st,i,1);
}
for(int i=1;i<=n;i++)
{
addEdge(m+i,ed,1);
}
for(int i=0;i