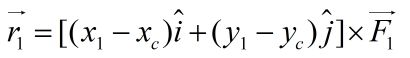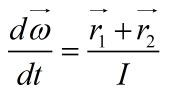Introduction and Backgroud
As we have known,Hyperion has an unusual shape,leading to its different behavior.Hyperion is shaped more like an egg and its orbit is choatic. We are now studying the behavior of our model for Hyperion for different initial conditions
The moon is named after Hyperion, the Titan god of watchfulness and observation – the elder brother of Cronus, the Greek equivalent of Saturn – in Greek mythology. It is also designated Saturn VII. The adjectival form of the name is Hyperionian.Hyperion's discovery came shortly after John Herschel had suggested names for the seven previously-known satellites of Saturn in his 1847 publication Results of Astronomical Observations made at the Cape of Good Hope.[9] William Lassell, who saw Hyperion two days after William Bond, had already endorsed Herschel's naming scheme and suggested the name Hyperion in accordance with it.[10] He also beat Bond to publication
---------------from wikipedia
Abstract
.This time we mainly discusses the Hyperion satellite orbiting Saturn with chaotic tumnling phenomena.
Main cody
The gravitational force on m1 can be written as
The torque on m1 is
The total torque on the moon is just e1+r2, then we can time derivative by
Putting all together
We simulate the phenomena, here is the code
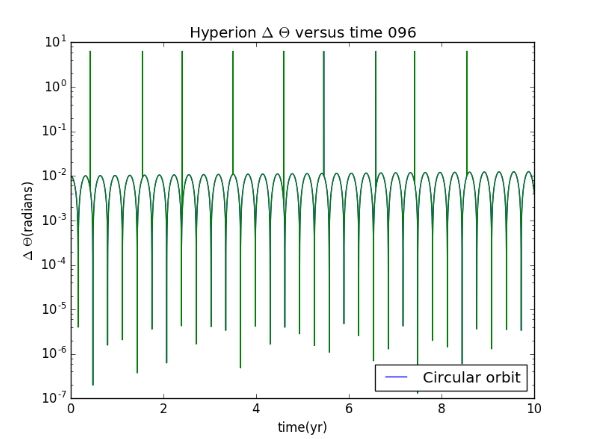
First, We think the behavior when the orbit is circular
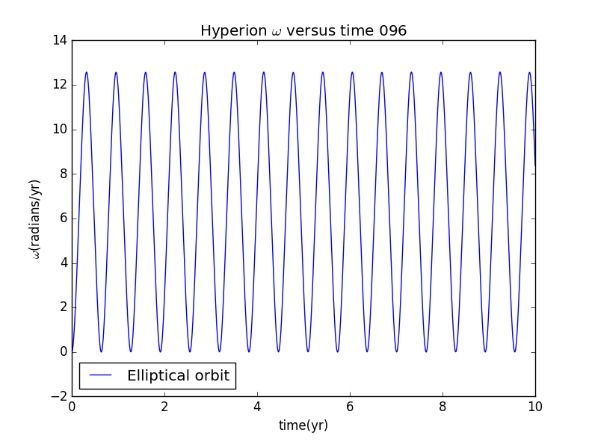
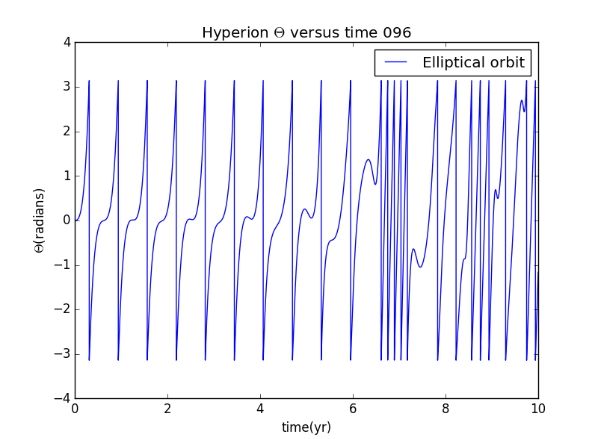
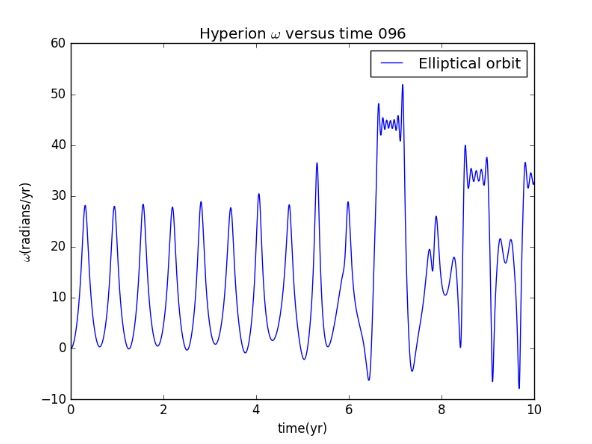
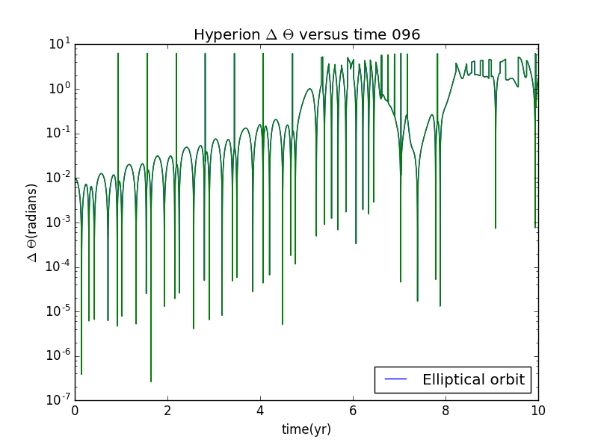
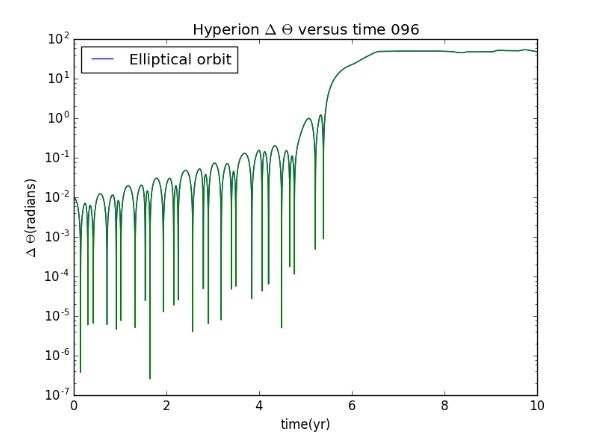
Secondly we consider the situation when the orbit is elliptical.(just change the size of theta)
So we can draw a conclusion that the chaotic phenomena would appear when the orbit changed into elliptical shape.
Then we are going to find the relation between the "theta" "t" and "V". Plot the difference between two results for θ(t) with different inital conditions.We use θ(0)=0 for one trajectory and θ(0)=0.01 for the other
So wen can find that when V_initial decreased, the Lyapunov exponent increased realatively
Reference
Thanks for chenruiyang's code
The link of Hyperion on WKI-pedia