Abstract
In this exercise, the motion of Hyperion will be discussed according to the instruction of Problem4.21.Hyperion, also known as Saturn VII,is distinguished by its irregular shape, chaotic rotation, and unexplained dumbball-like appearance.My work on Hyperion is just qualitative, aiming to show its chaotic during its orbit to Saturn.
Background
The model has been simplified as figure 4.16 in textbook.There are two forces acting on each of the masses, the force of the gravity from Saturn and the force from the rod. Since we are interested in the motion about the center of mass, the force from the rod does not contribute. The gravitational force on m1 can be written as
where Msat is the mass of Saturn, r1 is the distance from Saturn to m1, i and j are unit vectors in the x and y directions. The coordinates of the center of mass are (xc,yc), so that (x1-xc)i+(y1-yc)j is the vector from the center of mass to m1. The torque on m1 is then
with a similar expression for r2. The total torque on the moon is just r1+r2 and this is related to the time derivative of omega by:
Hence,we have
rc is the distance from the center of mass to Saturn.
The Main Body
First of all, if we restrain theta in
For point c(the center of mass), if it move in a circle, we can see:
If its trajectory is ellipse, we have:
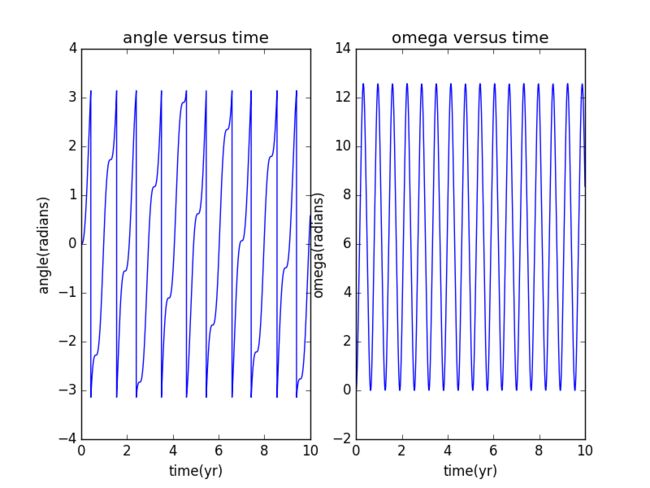
It is obviously that as for circular orbit, the motion is not chaotic,however, as for ellipse orbit, the result is very complicated and erratic, and appears to be chaotic.The abrupt vertical jumps in theta are due to our restriction that theta is -pi to pi.
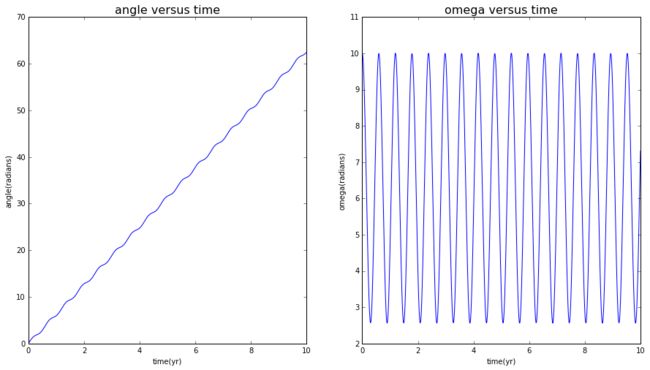
So we next remove this restriction, for circular orbit, we have:
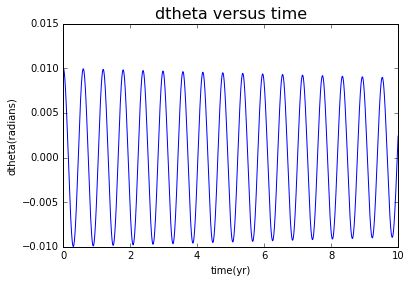
Futher more, we set two different initial conditions with theta(0)=0 and other on theta(0)=0.01, in all case the omega is zero.
we still find a regular wave.
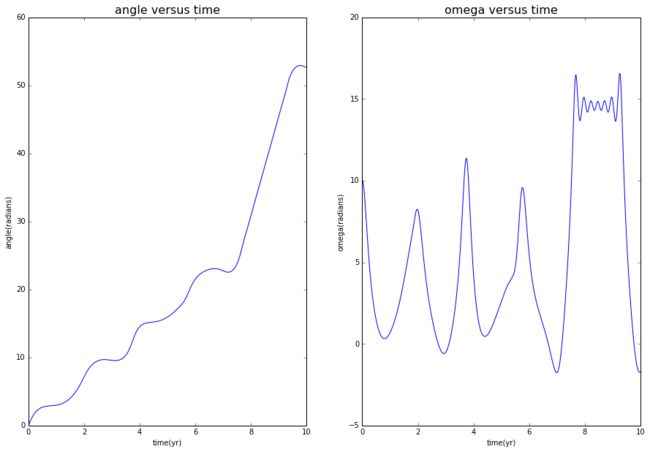
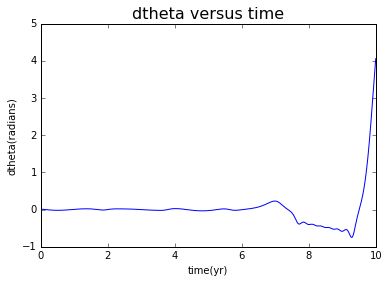
In the following step, with no doubt that we change circular orbit to ellipse orbit ,we have:
Compared to what I have done in circular orbit, this time chaos appear.Also, as time goes by, we can see dtheta have a rapid growth. To be more specific, if we contrast this to figures with the -pi to pi restriction, we gain tendency with more details.On the other hand, we can now get a clearer realization that one essential feature of a chaotic system is an extreme sensitivity to initial conditions.
click here to see the code
Reference
Wu Yuqiao's codes