普通大数乘法
普通大数乘法模拟两个数字竖式相乘,为了方便操作,数字的个位在数组的第0位,时间复杂度为O ( n² )
Bull Math
#include
#include
using namespace std;
const int MAXN=1200;
struct BigInt
{
int num[MAXN];
int len;//数字长度
void init()
{
memset(num,0,sizeof(num));
len=0;
}
void setVal(char *str)
{
len=strlen(str);
int index=0;
while(str[index]=='0'&&len>1)//去除前导零
{
len--;
index++;
}
for(int i=strlen(str)-1,j=0;i>=index;i--,j++)
{
num[j]=str[i]-'0';
}
}
void out()//数字打印
{
for(int i=len-1;i>=0;i--)
{
printf("%d",num[i]);
}
printf("\n");
}
static BigInt multi(BigInt a,BigInt b)
{
BigInt c;
c.init();
c.len=a.len+b.len;//a与b相乘的长度不超过a.len+b.len
for(int i=0;i1) c.len--;//去除前导0
if(c.num[c.len-1]==0&&c.len>1) c.len--;
return c;
}
};
int main()
{
BigInt a,b,c;
char v1[4500],v2[4500];
scanf("%s%s",v1,v2);
a.setVal(v1);
b.setVal(v2);
c=BigInt::multi(a,b);
c.out();
}
Karatsuba algorithm
以下内容为转载
- 概述
Karatsuba乘法是一种快速乘法。此算法主要用于两个大数相乘。普通乘法的复杂度是n2,而Karatsuba算法的复杂度仅为3nlog3≈3n1.585(log3是以2为底的)
取m = (n+1)/2,把x写成10m*a+b的形式,y写成10m*c+d的形式,则a, b, c, d都是m位整数(如果不足m位,前面可以补0)。
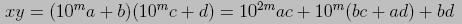
递归方程为T(n) = 4T(n/2) + O(n),其中系数4为四次乘法ac, bd, bc, ad,附加代价n为最后一个return语句的两次高精度加法。方程的解为T(n) = O(n^2),和暴力乘法没有区别。
Anatolii Karatsuba在1962年提出一个改进方法(并由Knuth改进):用ac和bd计算bc + ad,即:
bc + ad = (a + b)*(c + d)-ac - bd
这样一来,只需要进行三次递归乘法,即递归方程变为了T(n) = 3T(n/2)+O(n),解为T(n) = O(nlog3) = O(n^1.585),比暴力乘法快。 - 伪代码
procedure karatsuba(num1, num2)
if (num1 < 10) or (num2 < 10)
return num1*num2
/* calculates the size of the numbers */
m = max(size_base10(num1), size_base10(num2))
m2 = m/2
/* split the digit sequences about the middle */
x1, x0 = split_at(num1, m2)
y1, y0 = split_at(num2, m2)
/* 3 calls made to numbers approximately half the size */
z0 = karatsuba(x0,y0)
z1 = karatsuba((x1+x0),(y1+y0))
z2 = karatsuba(x1,y1)
return (z2*10^(2*m2))+((z1-z2-z0)*10^(m2))+(z0)
代码参考来源
#include
#include
using namespace std;
//增加前导零,加减法法对齐时用到
void addPreZero(string &num,int len)
{
while(len--)
{
num.insert(num.begin(),'0');
}
}
//num=num*10^len
void shiftString(string &num,int len)
{
if(num=="0") return ;//如果本身是0,不进行任何操作,否则最终结果会出现前导零
while(len--)
{
num.push_back('0');
}
}
//对齐
int makeSameLen(string &num1,string&num2)
{
int len1=num1.size();
int len2=num2.size();
if(len1>len2)
{
addPreZero(num2,len1-len2);
return len1;
}
else
{
addPreZero(num1,len2-len1);
return len2;
}
}
//减法
string minusString(string num1,string num2)
{
int len=makeSameLen(num1,num2);
int carray=0,currVal;
string res;
for(int i=len-1;i>=0;i--)
{
currVal=num1[i]-num2[i]+carray;
carray=0;
if(currVal<0)
{
currVal+=10;
carray=-1;
}
res.insert(res.begin(),currVal+'0');
}
//去掉前导零,只有减法才可能出现前导零,加法不会出现前导零,所以加法不用去
string::iterator it=res.begin();
while(it!=res.end()&&*it=='0') it++;
if(it==res.end()) return "0";
res.erase(res.begin(),it);
return res;
}
//加法
string addString(string num1,string num2)
{
int len=makeSameLen(num1,num2);
string res;
int carray=0,currVal;
for(int i=len-1;i>=0;i--)
{
currVal=num1[i]-'0'+num2[i]-'0'+carray;
carray=0;
if(currVal>9)
{
currVal-=10;
carray=1;
}
res.insert(res.begin(),currVal+'0');
}
if(carray) res.insert(res.begin(),'1');
return res;
}
string toString(int num)
{
if(num==0) return "0";
string res;
while(num)
{
res.insert(res.begin(),num%10+'0');
num/=10;
}
return res;
}
string Karatsuba(string num1,string num2)
{
int len=makeSameLen(num1,num2);
if(len==0) return "0";
if(len==1) return toString((num1[0]-'0')*(num2[0]-'0'));
int mid=len/2;
string a=num1.substr(0,mid),b=num1.substr(mid,len-mid);
string c=num2.substr(0,mid),d=num2.substr(mid,len-mid);
string z1=Karatsuba(a,c);
string z2=Karatsuba(b,d);
string z3=Karatsuba(addString(a,b),addString(c,d));
z3=minusString(z3,z1);
z3=minusString(z3,z2);
shiftString(z1,2*(len-mid));
shiftString(z3,len-mid);
return addString(addString(z1,z2),z3);
}
int main(){
int c;
string a,b;
cin>>a>>b;
cout< FFT大数乘法
大数乘法(快速傅立叶变换)上
大数乘法(快速傅立叶变换)下
#include
#include
#include
using namespace std;
const int MAXN=300010;
const double PI=3.141592653;
char s1[MAXN],s2[MAXN];
int ans[MAXN];
double retmp[MAXN],intmp[MAXN];
double rea[MAXN],ina[MAXN],reb[MAXN],inb[MAXN];
void FFT(double *reA,double *inA,int n,int flag)
{
if(n==1) return;
double rewm=cos(2*PI/n),inwm=sin(2*PI/n);
if(flag) inwm=-inwm;
double rew=1.0,inw=0.0;
//把下标为偶数的值按顺序放在前面,下标为奇数的值按顺序放在后面
int i,j,k;
for(i=0,k=1;klen2?len1:len2,base=1;
while(basei) rea[i]=(double)(s1[len1-i-1]-'0');
if(len2>i) reb[i]=(double)(s2[len2-i-1]-'0');
ina[i]=inb[i]=0.0;
}
//分别把向量a和向量b的系数转化为点值表示
FFT(rea,ina,len,0);
FFT(reb,inb,len,0);
//点值相乘得到向量c的点值表示
for(int i=0;i1) length--;
for(int i=length-1;i>=0;i--)
{
printf("%d",ans[i]);
}
printf("\n");
}
}