背景
在工程应用中经常会遇到一些复杂的非线性系统(我们航空发动机就是典型的强非线性模型),这些系统状态方程复杂,难以用数学方法准确建模。在这种情况下,可以建立BP神经网络表达这些非线性系统。该方法把未知系统看成黑箱,首先用系统输入输出数据训练BP神经网络,使网络能够表达该未知函数,然后用训练好的BP神经网络预测系统输出。
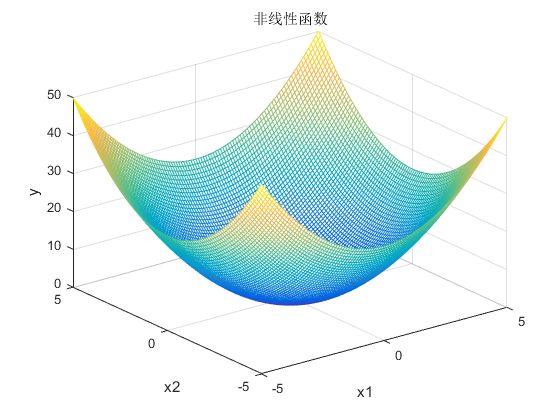
本文要拟合的非线性函数是
该函数的图形如下图1所示。
模型建立
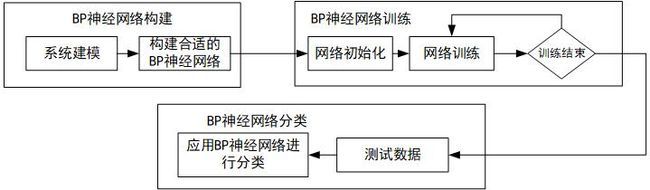
回顾上一篇文章建立BP网络的算法流程,进行具有非线性函数拟合的BP网络可以分为网络构建、训练和预测三步,如下图2所示。
BP神经网络构建根据要拟合的非线性函数特点确定BP网络结构,由于该非线性函数有两个输入参数,一个输出参数,所以BP网络结构可以设置为2-5-1,即输入层有2个节点,隐含层有5个节点,输出层有1个节点。
BP神经网络训练用非线性函数输入输出数据训练神经网络,使训练后的网络能够预测非线性函数输出。从非线性函数中随机得到2 000组输入输出数据,从中随机选择1 900组作为训练数据,用于网络训练,100组作为测试数据,用于测试网络的拟合性能。
神经网络预测用训练好的网络预测输出,并对预测结果进行分析。
MATLAB实现
1、数据选择和归一化
根据非线性函数方程随机得到该函数的2 000组输入输出数据,将数据存储在data.mat文件中,input是函数输入数据,output是函数输出数据。从输入输出数据中随机选取1 900组数据作为网络训练数据,100组作为网络测试数据,并对训练数据进行归一化处理。
%% 清空环境变量
clc
clear
%% 训练数据预测数据提取及归一化
%下载输入输出数据
load data input output
%从1到2000间随机排序
k=rand(1,2000);
[m,n]=sort(k);
%找出训练数据和预测数据
input_train=input(n(1:1900),:)';
output_train=output(n(1:1900));
input_test=input(n(1901:2000),:)';
output_test=output(n(1901:2000));
%训练样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
2、BP神经网络训练
用训练数据训练BP神经网络,使网络对非线性函数输出具有预测能力。
%% BP网络训练
% %初始化网络结构
net=newff(inputn,outputn,5);
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00004;
%网络训练
net=train(net,inputn,outputn);
3、BP神经网络预测
用训练好的BP神经网络预测非线性函数输出,并通过BP神经网络预测输出和期望输出,分析BP神经网络的拟合能力。
%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
%网络预测输出
an=sim(net,inputn_test);
%网络输出反归一化
BPoutput=mapminmax('reverse',an,outputps);
4、结果分析
%% 结果分析
figure(1)
plot(BPoutput,':og')
hold on
plot(output_test,'-*');
legend('预测输出','期望输出')
title('BP网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
%预测误差
error=BPoutput-output_test;
figure(2)
plot(error,'-*')
title('BP网络预测误差','fontsize',12)
ylabel('误差','fontsize',12)
xlabel('样本','fontsize',12)
figure(3)
plot((output_test-BPoutput)./BPoutput,'-*');
title('神经网络预测误差百分比')
errorsum=sum(abs(error));
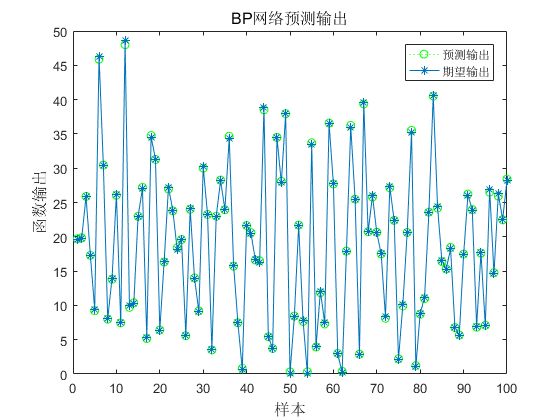
用训练好的BP神经网络预测函数输出,预测结果如下图3所示。
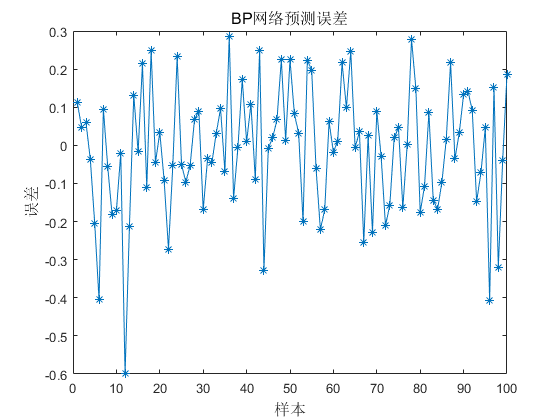
BP神经网络预测输出和期望输出的误差如下图4所示。
从图3和图4可以看出,虽然BP神经网络具有较高的拟合能力,但是网络预测结果仍有一定误差,某些样本点的预测误差较大。
改进网络
在上一篇文章中提到了调整隐含层节点数目、改变权值和阈值更新算法以及变学习率学习算法等方法,针对非线性拟合,BP神经网络的优化还可以使用多隐层的BP神经网络、改变激活函数等方法。