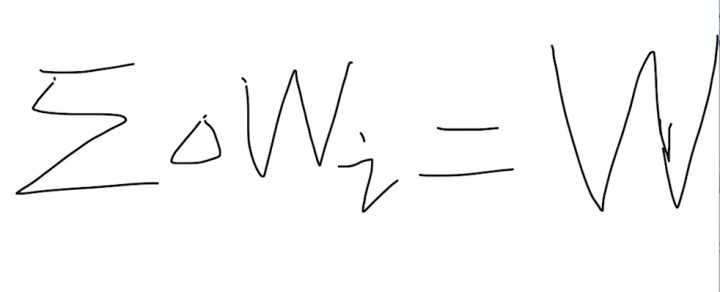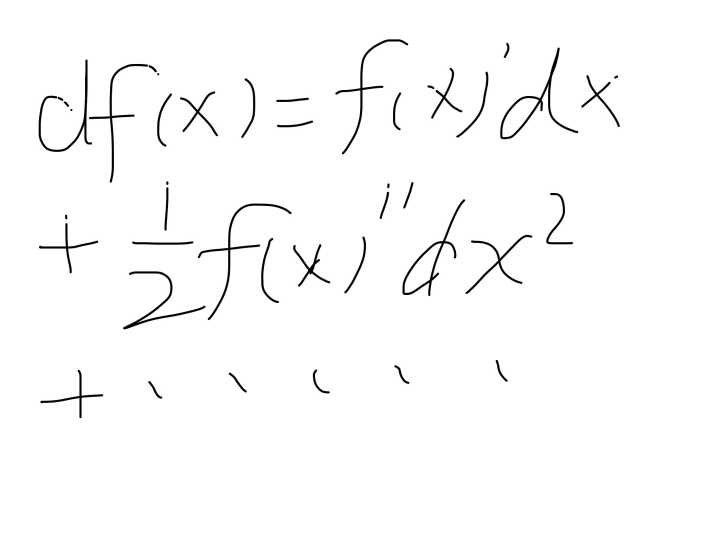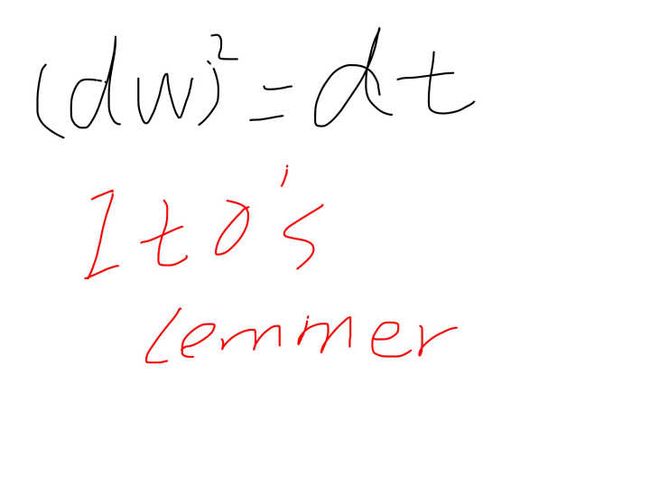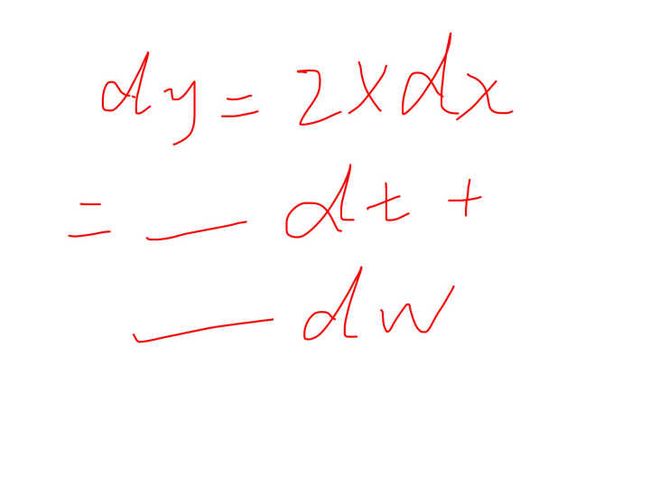伊藤定理
在日语里边什么藤往往是贵族的后裔,比如什么佐藤什么的,而我们今天要学习的就是伊藤定理,让我们一起去揭开他的神秘面纱吧.
在我们学习的微分方程里有三项:一个是-ax或者是△t,还有一个是YN△T,然后这时候我们把后边的yn△t看为△Wn
这时候我们定义一个积分,∑所有的I△Wi,我们把这个叫做大的W:
然后现在我们要研究一个更有趣的事实,就是如果让这样的i变成一个无穷的数的话,我们是不是可以把第一幅图中的这样的一个差分方程写成一个我们熟悉的微分方程,听起来有点困难,我们朝这个方向努力,也许它能够变成一个dw的形式而不是一个△w的形式,但是如果我们朝着这个方向再去努力,让他变得更加的连续的话,那这样的dw就会出现一个问题,dw是一个小量,而经过微分后第一个方程的t会变成dt,这时候dt也会变成一个小量,这两个小量是什么关系?这是一个非常trick的事情,这样其实会变成在N趋向于无穷的事情,但是这样会不会违背我们之前所说的概率论里边的极小时间段里这可能不是高斯分布,那我们真的让他趋向于无穷,这样它能够切换到极小,这时候会不会还原成不是高斯分布?其实不会的,因为假设在真实世界极小的时间段并非高斯分布,但是极小时间段的100倍是高斯分布,那接下来的性质我们已经脱离出来了,我们就是以宏观上来说他就是高斯分布,然后再把它切小,相当于一个以基础为前提的数学上的一个进化,所以这时候我们已经脱离真实世界了,我们再切小也是高斯分布因为他的宏观性质是一样的,而我们最终关心的是T时间,即在合理时间内的这样的一个涨跌的性质,所以这时候我们从自然界变成数学然后再回去,变成一个时间无限可分,但是在真实世界中时间并不是无限可分,分到普朗克时间就不能再分了,而在数学上是可以无限可分的,那现在我们关心的是,我们现在无限可分,这时候dw和dt是什么关系?
这时候我们猜想,是dw=dt么,还是说他们有某种正比的关系,还是说dw可能等于dt的平方?这才是我们关心的问题,首先我们刚才是知道每一个△w的平均值=0,并且△w的平方的平均值是△t,因为一个随机变量他的平均值等于0,因此他的平方的平均值就等于他的方差,而他的方差是△t,那这时候我们考虑一下,把这样的0到T的时间上的的△w²相加会怎么样?
这个时候我们考虑,当N趋向于无穷大的时候,我们是不是可以把它写成一个积分号从0-T,然后这边就变成积分的符号,
并且这时候还是高斯分布的,那么这时候有趣的事情来了,如果我们能够把它进行连续化,积分号其实是一个求和,求期望也就变成了一个数学操作,可能在数学分析级别的数学我们是不能把这个期望丢在里边的,但是在我们的工程用都是完全OK的,就是积分好的级数求和求期望能不能交换一样,我们认为是OK的,而从上边得推理我们知道,△W²等于△t,这时候我们的方差可以改为
而这些不等于别的,正是T,所以我们现在把重要的东西抽出来就会变成一个关于dw²的叠加,然后再去推理就会变成关于dt的叠加,而且这是对任意的T而言的,那么这时候总和每一个总和都是成立的话,他的每一个微元必须也精确地成立,所以这时候能够得到一个夸张的结论:dw²=dt,也就是说他的微元是一种平方相等的关系,而这个事情在高数里边是没有出现过的,我们还记得泰勒展开么?
而如果把这里的x换成t的话,他的第一项就是dt,没有比dt更小的项了,但是在随机微分方程里边,他的每一个求和的原,是可以有比dt更小的项,因为dw²就是等于dt,但是你又不能说dw²等于根下dt,因为你没法第一根号dt,所以这是随机微分方程跟普通的微分方程最大的区别,就是我们得到一个前所未有的奇怪的项,而这个奇怪的项会无处不在的影响我们,所以我们之前所有可能的高数级别的所有关于展开或者是微元的式子都需要改进或者修正,这是最精彩的部分,正是因为这一个部分解决了,所以后面推出了可以用来计算一切期权的balck_Scholes方程,这是一个基本的数学性质,而这个基本的数学性质就叫做伊藤引理,这是一个重要的引理,所以我们之后看见dw²就直接替换成dt就可以了.
所以我们把随机微分方程叫做SDE,(stochastic differential equation),就是在比如说常微分方程或者偏微分方程里面,我们关心的就是dx,dy,dt但是在随机微分方程里边我们关心的是dw,而dw是他最重要的一个特性,就是跟dt有关的我们会保留,然后dw是无处不在的,一定会引入的涨落,如果没有引入再涨落,就不是随机微分方程了,而他的dw²必须也要关注,那么接下来我们看一看我们以前认为是OK的结论要如何去修正:
现在我们拿一个简单的函数:y=x²,在普通的高等数学里边,y=x²的积分是dy=2xdx,那么现在如果x是由随机的dw存在的话,如果x是关于t的一个函数,因为随机过程总是要按照什么才能随机对不对,我们认为是关于时间随机,那么这时候这样的一个简单的方程应该要如何的写成一个关于时间的一个表达式:
为了明确,我们先把dx写成dt和dw的形式,这时候系数的话我们随便写,比如我们先给定一个f和g,是两个常数或者表达式
这个时候请大家求一下这个时候dy应该是多少?
当我们保留到一阶的情况下,我们就用我们最熟悉的东西去解决它然后再去替代,最熟悉的东西是因为我们知道dx是一阶的,所以如果我们不是对他直接保留到一阶的话,保留到二阶的话,会出现一个dx²,dx²会有一个dw²,dw²其实是一阶的,这意味着什么,意味着我们一开始就保留的泰勒级数的泰勒展开就应该要多保留一下,所以说在新的随机微分方程里边我们对一个函数的展开在第一步就应该展开到二阶,三阶我们就不管,因为dw的三次方可能就是二阶的,那dt的三次方就是三阶的,那我们只需要保留到原来的精度就可以了: