首先简单说一下为什么要用 btree ,大约两年前我们在数据打点这块引入了商业付费IP解析库“ipip.net”,用来将打点采集到的ip解析成地域和网络运营商,购买时官方宣称识别率在95%以上,而在我们实际数据测试显示只有82%左右;地域识别在营销宣传与广告投放应用中占有举足轻重的地位。
方案
为了解决上述问题,我们的优化思路大致是这样的:
- 在商业版基础上合并开源版的ip库,合并后的ip库作为基础版对外提供服务;
- 每天遍历日志数据收集未解析的ip,通过调用开源ip解析服务补充错误数据(如阿里、腾讯、百度、360等服务商提供的在线api)
这里会涉及到一个问题,日志打点服务对性能要求非常高,如何存储ip库、如何设计ip数据的存储结构是非常重要的
什么是BTree
B树是一种常见的树形设计结构,是二叉树的一种特殊应用,常用在磁盘存储与数据库索引存储的设计中;BTree通常也叫B-Tree,是平衡二叉树(其中B是balance的意思),它每层节点数不止2个(m/2+1 <= 节点数 <= m-1 ;其中m代表m阶B树),且每个分支深度是相同的,除叶子节点外的其它节点不存储数值,只存储关键字和指针。
BTree能解决哪些问题
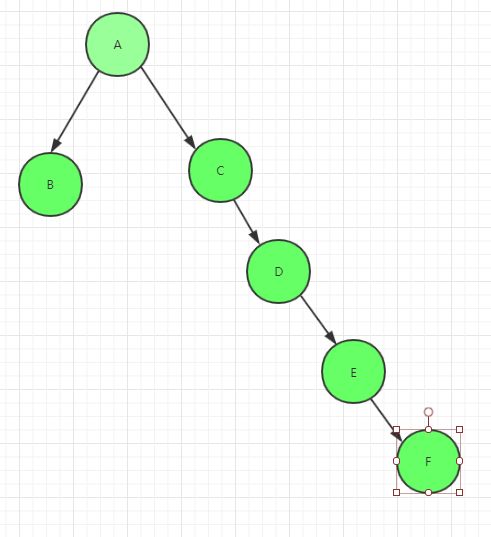
大学计算机数据导论都学过二叉树和链表的设计,这两种数据结构其实在工业界并不常用,原因很简单,链表数据结构在 大数据面前存在严重的性能问题,而二叉树如果不能保证各分支深度一致的话很容易变成链表结构,导致性能下降。
如何设计
二分查找在进行数据检索时效率非常高,但如果数据结构如上图所示,就很难保证较高的查询性能了;这时就要用到平衡二叉树了,我们将通过一个简单的4阶平衡二叉树进行讲解:
假设我们插入数据的顺序如下:
st.put("A", "1");
st.put("D", "4");
st.put("M", "12");
st.put("C", "3");
st.put("G", "6");
st.put("B", "2");
st.put("E", "5");
st.put("H", "7");
st.put("J", "8");
st.put("L", "8");
st.put("Z", "32");
st.put("N", "13");
st.put("K", "17");
st.put("O", "18");
st.put("Q", "19");
st.put("P", "21");
st.put("I", "22");
st.put("S", "23");
st.put("Y", "24");
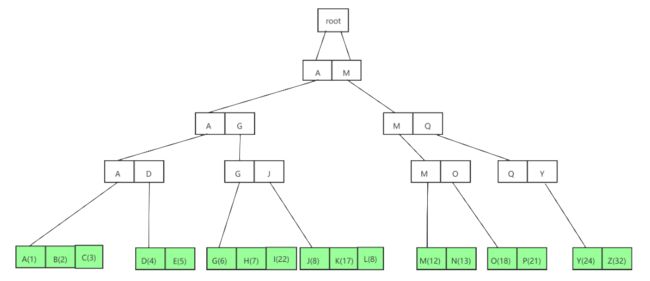
按照上面的数据进行构建,形成的btree是这样的
- 上述节点有三种:1、root 节点,仅仅存储第一层节点的指针; 2、叶子节点,存储key 和 value 没有下层节点指针 ; 3、中间的所有节点,存储key 和下层节点的指针,不存储value
- 每次节点的元素个数 满足 [m/2+1, m-1],且按照key从小到大排列
- 每个分支的深度都是一致的
构建流程
这里给出A-J数据插入构建流程
Java实现
package com.eqxiu.crawler;
class BTree, Value> {
private static final int NODE_MAX_CHILD = 4; // max children per B-tree node = M-1
private Node root; // root of the B-tree
private int treeHeight; // height of the B-tree
private int kvNum; // number of key-value pairs in the B-tree
/* helper B-tree node data type */
private static final class Node {
private int childNum; // number of children
private Entry[] children = new Entry[NODE_MAX_CHILD]; // the array of children
private Node(int k) { childNum = k; } // create a node with k children
}
// internal nodes: only use key and next
// external nodes: only use key and value
private static class Entry {
private Comparable key;
private Object value;
private Node next; // helper field to iterate over array entries
public Entry(Comparable key, Object value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
// constructor
public BTree() { root = new Node(0); }
// return number of key-value pairs in the B-tree
public int size() { return kvNum; }
// return height of B-tree
public int height() { return treeHeight; }
// search for given key, return associated value; return null if no such key
public Value get(Key key) { return search(root, key, treeHeight); }
private Value search(Node x, Key key, int ht) {
Entry[] children = x.children;
// external node
if (ht == 0) {
for (int j = 0; j < x.childNum; j++) {
if (eq(key, children[j].key)) return (Value) children[j].value;
}
}
// internal node
else {
for (int j = 0; j < x.childNum; j++) {
if (j+1 == x.childNum || less(key, children[j+1].key))
return search(children[j].next, key, ht-1);
}
}
return null;
}
// insert key-value pair
// add code to check for duplicate keys
public void put(Key key, Value value) {
Node u = insert(root, key, value, treeHeight);
kvNum++;
if (u == null) return;
// need to split root
Node t = new Node(2);
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
treeHeight++;
}
private Node insert(Node h, Key key, Value value, int ht) {
int j;
Entry t = new Entry(key, value, null);
// external node
if (ht == 0) {
for (j = 0; j < h.childNum; j++) {
if (less(key, h.children[j].key)) break;
}
}
// internal node
else {
for (j = 0; j < h.childNum; j++) {
if ((j+1 == h.childNum) || less(key, h.children[j+1].key)) {
Node u = insert(h.children[j++].next, key, value, ht-1);
if (u == null) return null;
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
for (int i = h.childNum; i > j; i--) h.children[i] = h.children[i-1];
h.children[j] = t;
h.childNum++;
if (h.childNum < NODE_MAX_CHILD) return null;
else return split(h);
}
// split node in half
private Node split(Node h) {
Node t = new Node(NODE_MAX_CHILD/2);
int hNum = (int)(Math.ceil(NODE_MAX_CHILD*1.0/2));
h.childNum = hNum;
for (int j = 0; j < NODE_MAX_CHILD/2; j++)
t.children[j] = h.children[hNum+j];
return t;
}
// for debugging
public String toString() {
return toString(root, treeHeight, "") + "\n";
}
private String toString(Node h, int ht, String indent) {
String s = "";
Entry[] children = h.children;
if (ht == 0) {
for (int j = 0; j < h.childNum; j++) {
s += indent + children[j].key + " " + children[j].value + "\n";
}
}
else {
for (int j = 0; j < h.childNum; j++) {
if (j > 0) s += indent + "(" + children[j].key + ")\n";
s += toString(children[j].next, ht-1, indent + " ");
}
}
return s;
}
// comparison functions - make Comparable instead of Key to avoid casts
private boolean less(Comparable k1, Comparable k2) {
return k1.compareTo(k2) < 0;
}
private boolean eq(Comparable k1, Comparable k2) {
return k1.compareTo(k2) == 0;
}
/*************************************************************************
* test client
*************************************************************************/
public static void main(String[] args) {
BTree st = new BTree();
// st.put("www.cs.princeton.edu", "128.112.136.12");
st.put("D", "4");
st.put("M", "12");
st.put("C", "3");
st.put("A", "1");
st.put("G", "6");
st.put("B", "2");
st.put("E", "5");
st.put("H", "7");
st.put("J", "8");
st.put("L", "8");
st.put("Z", "32");
st.put("N", "13");
st.put("K", "17");
st.put("O", "18");
st.put("Q", "19");
st.put("P", "21");
st.put("I", "22");
st.put("S", "23");
st.put("Y", "24");
System.out.println("cs.princeton.edu: " + st.get("Z"));
System.out.println(st.size());
}
}