新冠病毒Logistic增长模型:中国+钻石公主号游轮
Rimmer 博士是一位退休的心脏病专家,自1988年以来一直使用Mathematica。他对数学统计,金融市场,全球定位系统,信息知识和医学感兴趣;他在 Mathematica Journal和Wolfram演示项目上发表了很多文章。
新型冠状病毒的资源&更新(中国、美国、全世界的数据):https://wolfr.am/coronavirus
Logistic增长模型
逻辑 (Logistic) 增长由一个微分方程定义:
f(t)/t==k f(t) (1-f(t)/L)
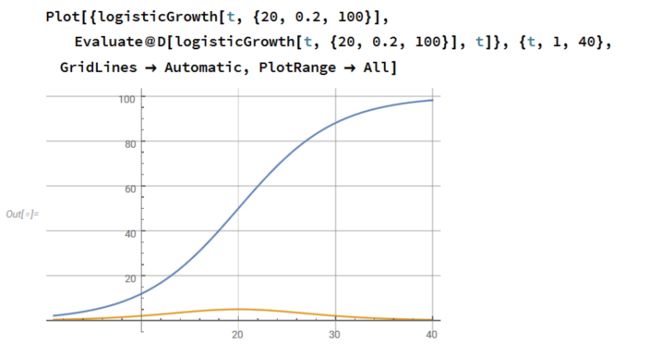
其中k是一个连续增长率,L是增长的界限,也就是说f(t)不能超过L。当f(t)与L小相关,则(1-f(t)/L)接近于1。初始增长与带指数增长率k的f(t)成比例。当f(t)到达L,增长率为0,增长结束。如果我们要求L和k为正数,则增长率总是正的。
这个模型最开始用于人口增长,概念是有一个空间可以支持的最大人口L,在这个空间中人口不能增长超过这个最大值。在传染病的流行病学控制中,有一个类似的模型,用于限定感染和潜伏人口,这样这些人口就不能向更大数量的人群传染疾病。在疾病爆发的初期,这个过程需要花费时间来完成,因为不能很好的掌握潜伏者的人口数量。但是主要概念是限制传染者和潜伏者,将他们隔离起来,这样的话L就会比未接触疾病的人口数量小很多。接触者互相隔离也很重要。如果控制的好,那么病毒可以传播的人口则会非常有限。如果传染不能接触到所有人群,那么病毒的易传染级别就没有那么重要。如果没有做好隔离,那么在有限空间内,比如在没有乘客可以下船的游轮上,传染的风险就会增加。
这证明了微分方程的解。
边界条件,f(t0) == L/2,将t0设为增长率最大的传染点。
函数给出了一个Sigmoid生长曲线,也显示了一阶导数。
有了参数替代,Logistic增长函数变成了LogisticDistribution函数。
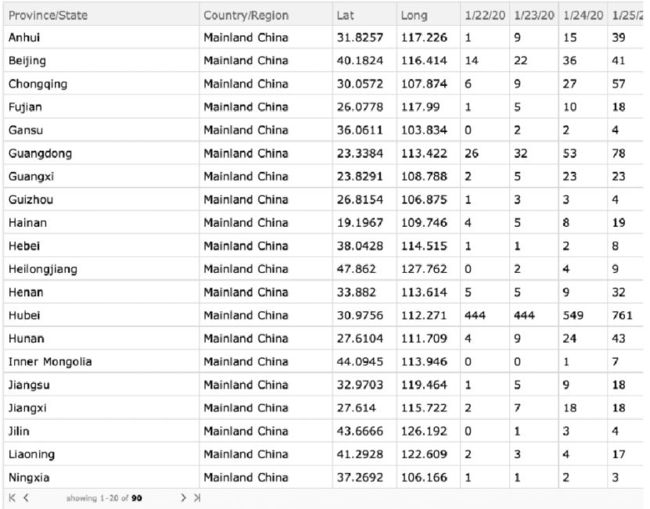
数据源
https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series
数据也可以用ResourceData["Epidemic Data for Novel Coronavirus COVID-19"]找到;GitHub数据好像也是一样的。对于模型来说,GitHub数据的格式更简单。
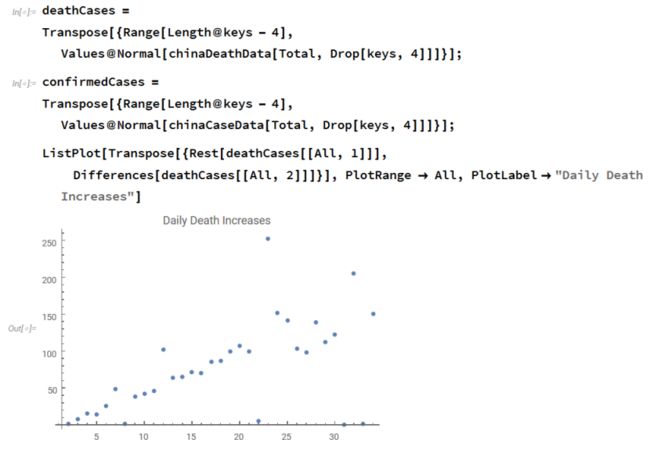
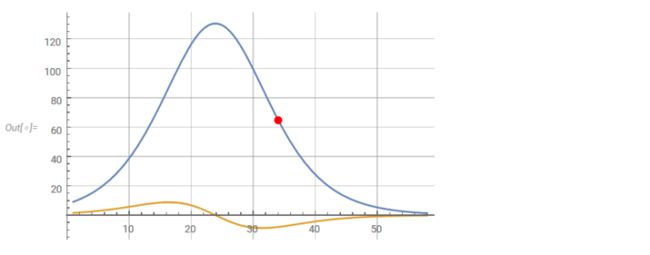
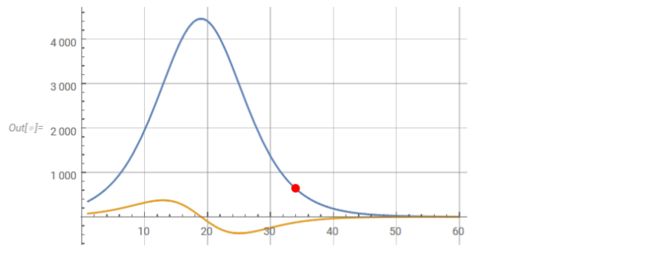
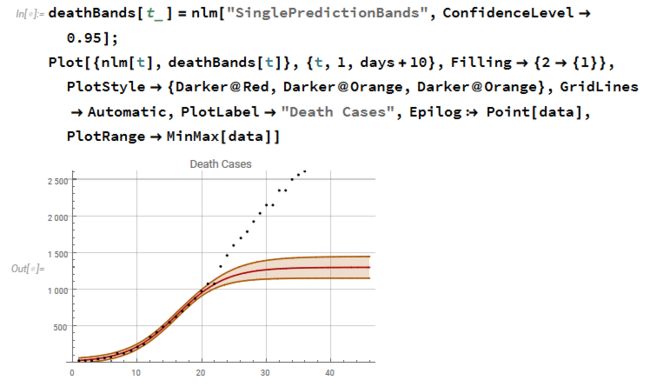
假设当每天病例降至最后的整数值就标志着这个流行病结束,这样流行病计算也就结束了。图中的红点显示了在一阶导数曲线上的当前点。二阶导数曲线也在图上显示。
假设当每天病例降至最后的整数值就标志着这个流行病结束,这样流行病计算也就结束了。图中的红点显示了在一阶导数曲线上的当前点。二阶导数曲线也在图上显示。
下一个部分不包括湖北省的数据,这些数据中确诊病例技术方法有时基于临床诊断而非实验室判断。还不是很清楚数据库是否随着确诊而更新。但是不管如何其他省份的数据,体量都小得多,而且更匹配这个模型。
假设当每天病例降至最后的整数值就标志着这个流行病结束,这样流行病计算也就结束了。图中的红点显示了在一阶导数曲线上的当前点。二阶导数曲线也在图上显示。
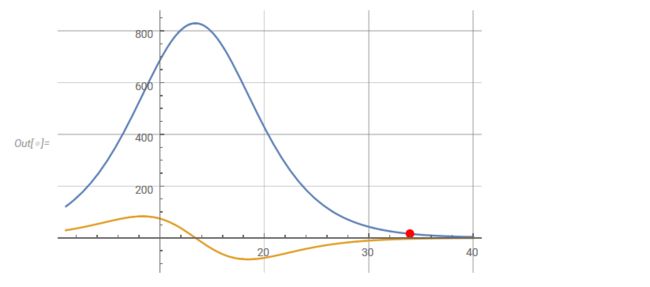
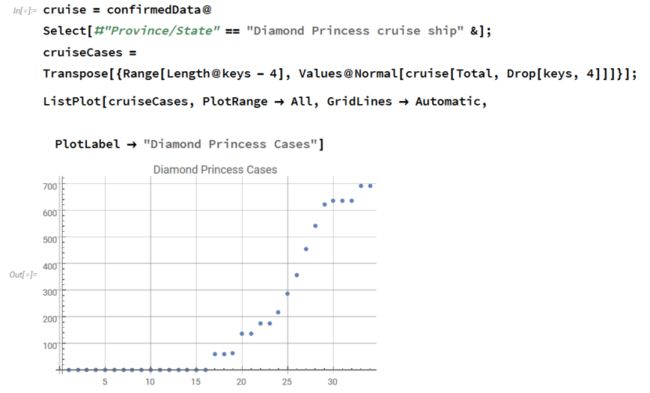
钻石公主号游轮
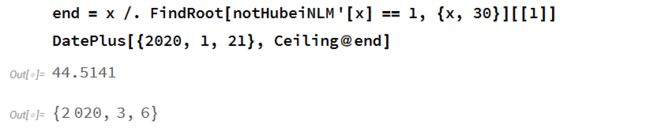
游轮上显著更大的k和更晚的t0说明相比起让健康的人下船并隔离疑似和感染者而言,限制下船可能引起更多人被感染。
用微分方程拟合数据
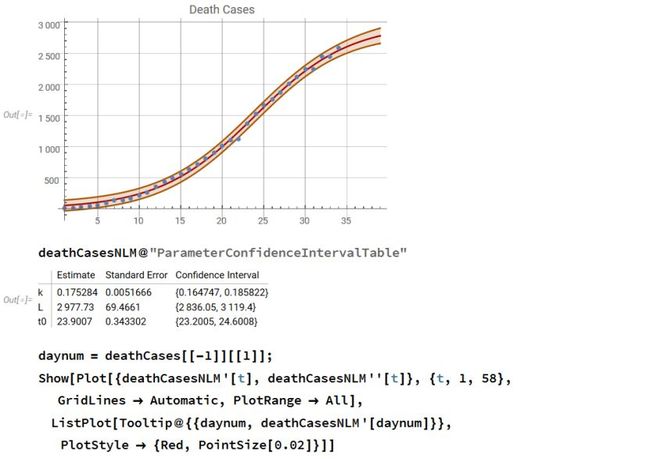
这个列表计算了基于微分方程f'[t]==k f[t] (1-f[t]/L)的一阶导数,直接使用数据:
现在我们获取了t0。
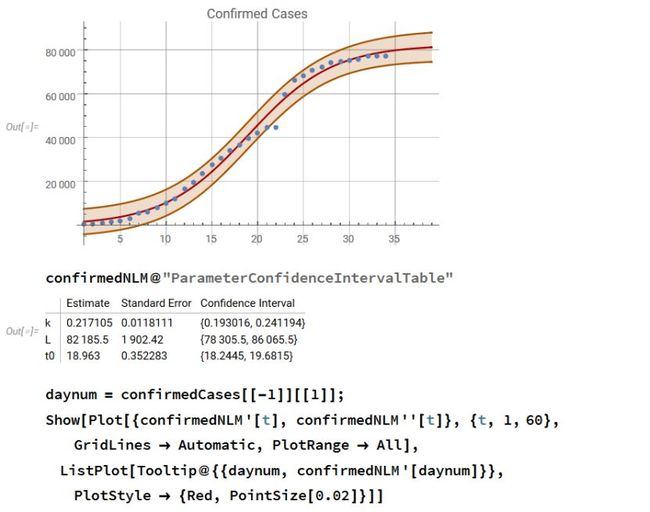
这个图比较了拟合和原数据。
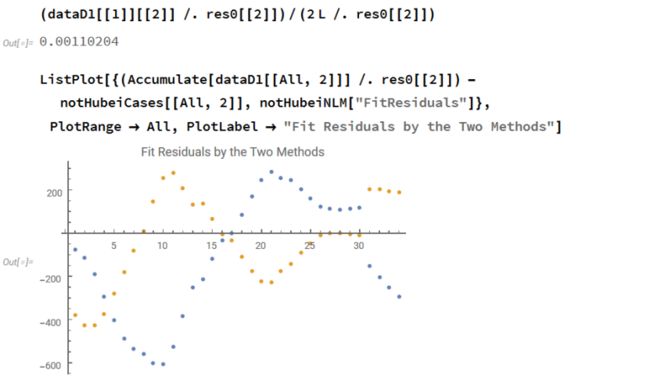
我很惊讶这个方法会提供这样一个精确的拟合,因为Accumulate[]并不是一个非常精确的数值积分法,但是导数都在数据点计算,所以这是一个黎曼中点积分,且加到每个点的系统性错误应该是一阶导数点除以2L的数量级,如下所示。
参数可以用数据的微分公式求出这件事说明,数据并不是被生硬地塞进一条曲线,数据背后的理论也嵌入了数据。如果随着数据增多这个预测依然成立,这就会是一个非常有用的模型。
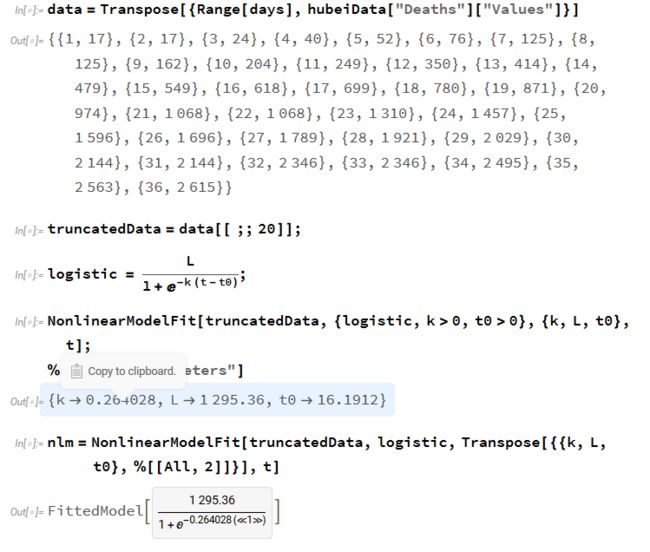
如果使用数据中的一部分,比如湖北省的数据,这个Logistic模型就会给出非常不同的结果。比如,假设现在是爆发后的第20天。如果我们使用头20天的可用数据,得到的模型并不能预测接下来的16天发生的情况。
A:
这个流行病开始时候的数据可能并不是很准确。有一些基本的数值上的原因:在早期的数据的信息中只有2位或3位有效数字,而后来的数字精度更高。但是最主要的原因是,早期的数据可能不是很准确,尤其是在湖北,那些实验室的数据很快就被取代。在中间的某个时候就不再用实验室数据了,WHO处的信息说明这些死亡病例数量只是实验室确认的病例。后面他们又一次性地加上了其他死亡病例数据,导致累计数据大幅上升。现在应该尝试使用最近的数据,这些数据又更多信息并且更加精确。并随着数据累计看一看连续拟合情况。
然后用ListPlot看连续参数,看看这些参数是否随着时间的推移可以稳定。给NonlinearModelFit一些合理的起始参数也是个不错的想法。
Rimmer 博士还对意大利和韩国的疫情进行了分析:
https://community.wolfram.com/groups/-/m/t/1887823
中国模型的更新:
https://community.wolfram.com/groups/-/m/t/1890271
Wolfram 部署了疫情交互式仪表板,追踪病毒最新传播情况
公司名称:北京哲想软件有限公司
北京哲想软件官方网站:www.cogitosoft.com
北京哲想软件微信公众平台账号:cogitosoftware
北京哲想软件微博:哲想软件
北京哲想软件邮箱:[email protected]
销售(俞先生)联系方式:+86(010)68421378
微信:18610247936 QQ:368531638