之前我们已经讲了代价函数了,这节我们讲代价函数J最小化的梯度下降法。
梯度下降是很常用的算法。它不仅被用在线性回归上,还被广泛应用于机器学习的众多领域。
下面是问题概述。我们有一个函数J(θ0,θ1),这也许是个线性回归的代价函数,也许是个需要最小化的其他函数。我们需要用一个算法,来最小化函数J(θ0,θ1)。
实际上,梯度下降算法可以应用于更一般的函数,如J(θ0,θ1,θ2,......θn),你希望可以在θ0到θn之上最小化此函数。但是为了简化,我们这里只用θ0,θ1两个参数。
梯度下降算法的基本思想是:首先给定θ0和θ1初始值(其实给定多少都不重要),但通常都设θ0=0,θ1=0。然后,我们不停地一点点地改变θ0和θ1,来使J(θ0,θ1)变小。直到我们找到J的最小值或者局部最小值。
下面我们通过图片来直观地看一下它是怎么工作的。
![[斯坦福大学2014机器学习教程笔记]第二章-梯度下降_第1张图片](http://img.e-com-net.com/image/info8/3c7717c016fd45e089ba6b3e0bd51d88.jpg) 首先我们先从θ0和θ1的某个值出发。想象一下你正站立在山的这一点上,站立在你想象的公园这座红色山上,在梯度下降算法中,我们要做的就是旋转360度,看看我们的周围,并问自己要在某个方向上,用小碎步尽快下山。这些小碎步需要朝什么方向?如果我们站在山坡上的这一点,你看一下周围,你会发现最佳的下山方向,你再看看周围,然后再一次想想,我应该从什么方向迈着小碎步下山?然后你按照自己的判断又迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。我们在刚刚出发点右边再出发一次,这时我们得到另外一个局部最低点的位置。
首先我们先从θ0和θ1的某个值出发。想象一下你正站立在山的这一点上,站立在你想象的公园这座红色山上,在梯度下降算法中,我们要做的就是旋转360度,看看我们的周围,并问自己要在某个方向上,用小碎步尽快下山。这些小碎步需要朝什么方向?如果我们站在山坡上的这一点,你看一下周围,你会发现最佳的下山方向,你再看看周围,然后再一次想想,我应该从什么方向迈着小碎步下山?然后你按照自己的判断又迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。我们在刚刚出发点右边再出发一次,这时我们得到另外一个局部最低点的位置。
我们就会发现,如果你的起始点偏移了一些,你会得到一个完全不同的局部最优解。这就是梯度下降算法的一个特点。
这是梯度下降算法的定义。
我们要更新参数θj为θj减去α乘以后面的那一部分。我们将会反复做这一步,直至收敛。
注意:1.我们使用符号:=表示赋值。
2.α是一个被称为学习率的数字。α决定了当梯度下降时,我们迈出的步子有多大。如果α很大的话,那么梯度下降就很迅速。如果α很小的话,那么梯度下降就很缓慢。
在梯度下降算法中,还有一个更微妙的问题,梯度下降中,我们要更新θ0和θ1 ,当j=0 和j=1时,会产生更新,所以你将更新J(θ0)和J(θ1)。实现梯度下降算法的微妙之处是,在这个表达式中,如果你要更新这个等式,你需要同时更新θ0和θ1,我的意思是在这个等式中,我们要这样更新:
θ0更新为θ0减去某项,并将θ1更新为θ1减去某项 。
实现方法是:你应该计算公式右边的部分,通过那一部分计算出θ0和θ1的值,然后同时更新θ0和θ1。
进一步地说,我们让temp0和temp1分别等于这两个式子。首先先计算公式右边的这一个部分,然后将值存入temp0和temp1中。这样,我们就可以同时更新θ0和θ1了。如下图左侧。
而右侧的计算是错的,因为它并没有做到同步更新。左右两边的区别就是,当我们计算temp1的值的时候,左边是用的更新之前θ0的值,右边用的是更新之后θ0的值,从而导致最后的temp1的值是不一样的。
![[斯坦福大学2014机器学习教程笔记]第二章-梯度下降_第2张图片](http://img.e-com-net.com/image/info8/61de126146a5444f973c39a79bea7181.jpg)
![[斯坦福大学2014机器学习教程笔记]第二章-梯度下降_第3张图片](http://img.e-com-net.com/image/info8/66282ba9273a4cc1aa1ca04a74514774.jpg)
![[斯坦福大学2014机器学习教程笔记]第二章-梯度下降_第4张图片](http://img.e-com-net.com/image/info8/8006ec0176a64a09bc35bd2f87bcf8b7.jpg)
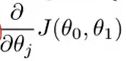
![[斯坦福大学2014机器学习教程笔记]第二章-梯度下降_第5张图片](http://img.e-com-net.com/image/info8/763b51b755424f9abb8fe6d3b7ce3744.jpg)