- 哈夫曼编码
- 哈夫曼树的相关概念
- 构造哈夫曼树
- 模拟构造
- 算法实现
- 结点结构体定义
- 代码实现
- Select 函数样例
- 根据哈夫曼树求哈夫曼编码
- 算法解析
- 代码实现
- 应用举例
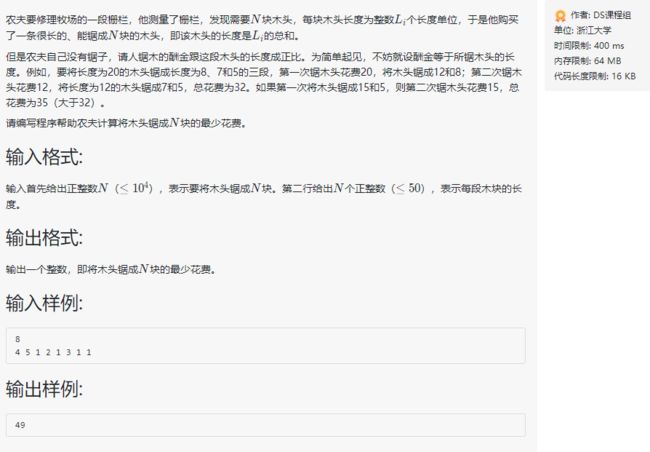
- 修理牧场(哈夫曼树实现)
- 情景模拟
- 代码实现
- 参考资料
哈夫曼编码
我们都知道使用电报来传递信息在上个世纪来说是很自然的,但是由于技术问题,使得远距离通信的数据传输效率显得极其重要,美国数学家哈夫曼研究出哈夫曼编码能够使得数据传输得到优化。例如我现在要传递信息 “ABBCCCDDDDEEEEE”,如果利用二进制编码来实现的话,就是传递“000 001 001 010 010 010 011 011 011 011 100 100 100 100 100”,有 45 个字符,但是我们观察到这个编码中有 5 个字母,每个字母出现的频率都不一样,这时我们就开始思考了,如果我们用一些其他的编码去组织这 5 种字符,让出现次数较多的字母用简单的代号去表示,这样会不会使得传递较少的数据,传达同样多的消息呢?
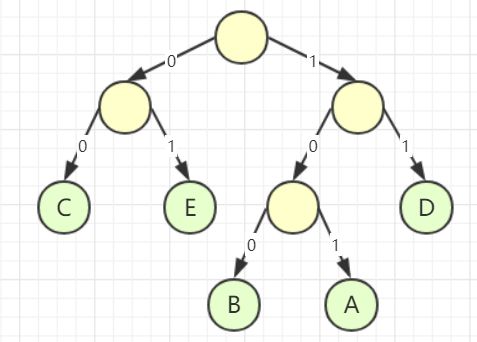
如图所示,我们拥有了这么一棵二叉树,我们发现这棵二叉树在两个结点间有个数字,我们用这些数字的组合来构造新密码。
| 字母 | 编码 |
|---|---|
| A | 101 |
| B | 100 |
| C | 00 |
| D | 11 |
| E | 01 |
那么“ABBCCCDDDDEEEEE”编码的结果就是“101 100 100 00 00 00 11 11 11 11 01 01 01 01 01”共 33 个字符,相比原来的 45 个字符而言已经有不小的进步了。那么你可能要问了,这么做读取的信息会不会出现二义性呢?答案是不会的,例如我收到了“011100100101”这个编码,你对照上文的二叉树,按照编码顺序从根结点向下解读,读取的结果是“EDCBA”,没有二义性。
这种巧妙的方法就是哈夫曼编码,而我们用来解密的二叉树就被成为哈夫曼树。与编码对应的哈夫曼编码生成的方式是,获取需要编码的字符集,将各个字符在数据中出现的次数整合为一个集合,以字符集作为叶子结点,以对应的频率作为相应叶子结点的权值来构造一棵二叉树,二叉树树的左分支代表 0,右分支代表 1,则从根结点到叶子结点所经过的路径分支组成的 0 和 1 的序列便为该结点应字符的哈夫曼编码。
1951年,哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是,寻找最有效的二进制编码。由于无法证明哪个已有编码是最有效的,哈夫曼放弃对已有编码的研究,转向新的探索,最终发现了基于有序频率二叉树编码的想法,并很快证明了这个方法是最有效的。由于这个算法,学生终于青出于蓝,超过了他那曾经和信息论创立者香农共同研究过类似编码的导师。哈夫曼使用自底向上的方法构建二叉树,避免了次优算法Shannon-Fano编码的最大弊端──自顶向下构建树。——百度百科
哈夫曼树的相关概念
哈夫曼树又称最优二叉树,是在路径带权的情况下长度最短的树,在实际中有广泛的用途。我们先来看一些概念的定义:
| 概念 | 定义 |
|---|---|
| 路径 | 从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径 |
| 路径长度 | 路径上的分支数目 |
| 树的路径长度 | 从树根到每一结点的路径长度之和 |
| 权 | 赋予某个实体的一个量,是对实体的某个或某些属性的数值化描述。在数据结构中,实体有结点(元素)和边(关系)两大类,所以对应有结点权和边权。结点权或边权具体代表什么意义,需要具体问题具体分析。如果在一棵树中的结点上带有权值,则对应的就有带权树等概念。 |
| 结点带权路径长度 | 从该结点到树根之间的路径长度与结点上权的乘积 |
| 树的带权路径长度 | 树中所有叶子结点的带权路径长度之和,通常记作 WPL |
我们先暂停一下,看个例子理解 WPL,假设有如下两个带权的二叉树:
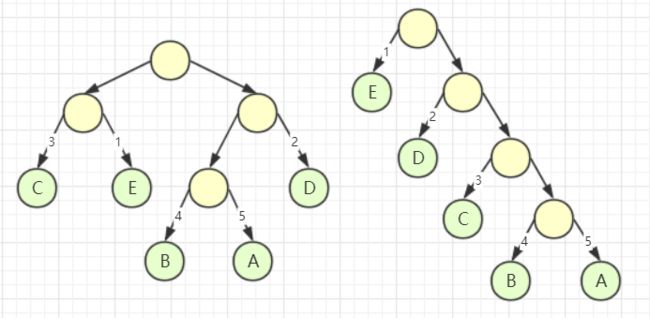
左树 WPL:1 × 2 + 3 × 2 + 2 × 2 + 4 × 3 + 5 × 3 = 39
右树 WPL:1 × 1 + 2 × 2 + 3 × 3 + 4 × 4 + 5 × 4 = 50
理解了上述概念,描述哈夫曼树就简单了,所谓哈夫曼树就是当我有 m 个权值的时候,构造一棵含有 n 个叶结点的二叉树,每个叶结点都设有一个权,当带权的路径长度 WPL 最小的二叉树称为哈夫曼树。
构造哈夫曼树
模拟构造
现在我们拥有 4 个给定权值,拥有 4 个结点,现在要把这四个结点构造成哈夫曼树。
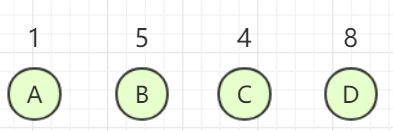
首先我们先要把这些结点抽象成 4 棵只有根节点的二叉树,这二叉树构成了一个森林。现在我从森林中选择 2 棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,而且这新的二叉树的根结点的权为左右子树上根结点权的和,并删除这两个被归并的二叉树,将新的二叉树归并到森林中,如图所示。
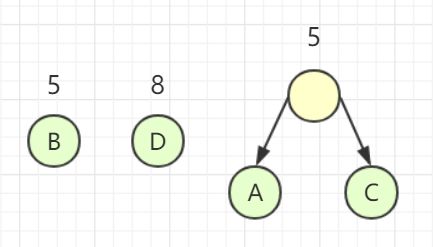
重复上述操作,直至仅剩一棵二叉树,所得的二叉树即为哈夫曼树。这是因为我们每次都选择权较小的结点,从而保证了权较大的结点更加靠近根结点,当我们计算 WPL 时自然就会得到最小带权路径长度。这很明显是使用了贪心算法。
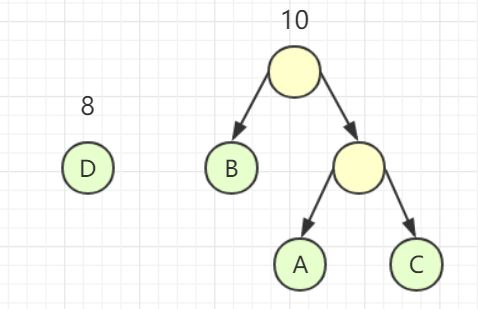
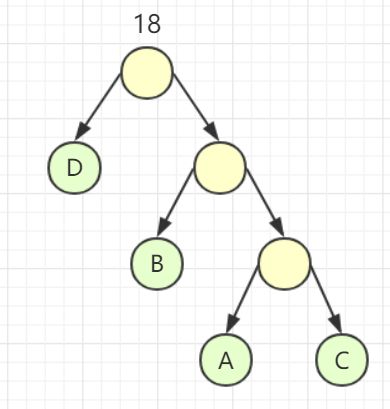
再来看个例子:
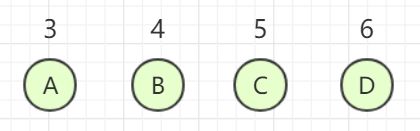
构造出的哈夫曼树为:
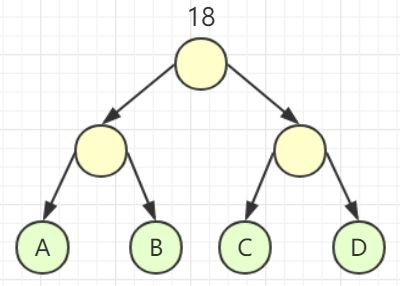
算法实现
结点结构体定义
由于哈夫曼树中不会出现度为 1 的结点,而且一棵有 n 个叶结点的哈夫曼树的总结点数为 2n - 1 个,因此我们可以使用顺序存储结构来实现。一个结点除了要存储权值,还要将结点的双亲的孩子结点都描述清楚,因此需要 3 个游标来进行描述。
typedef struct{
int weight; //权值
int parent,lchild,rchild; //指向双亲、左右孩子结点的游标
}HTNode,*HuffmanTree;
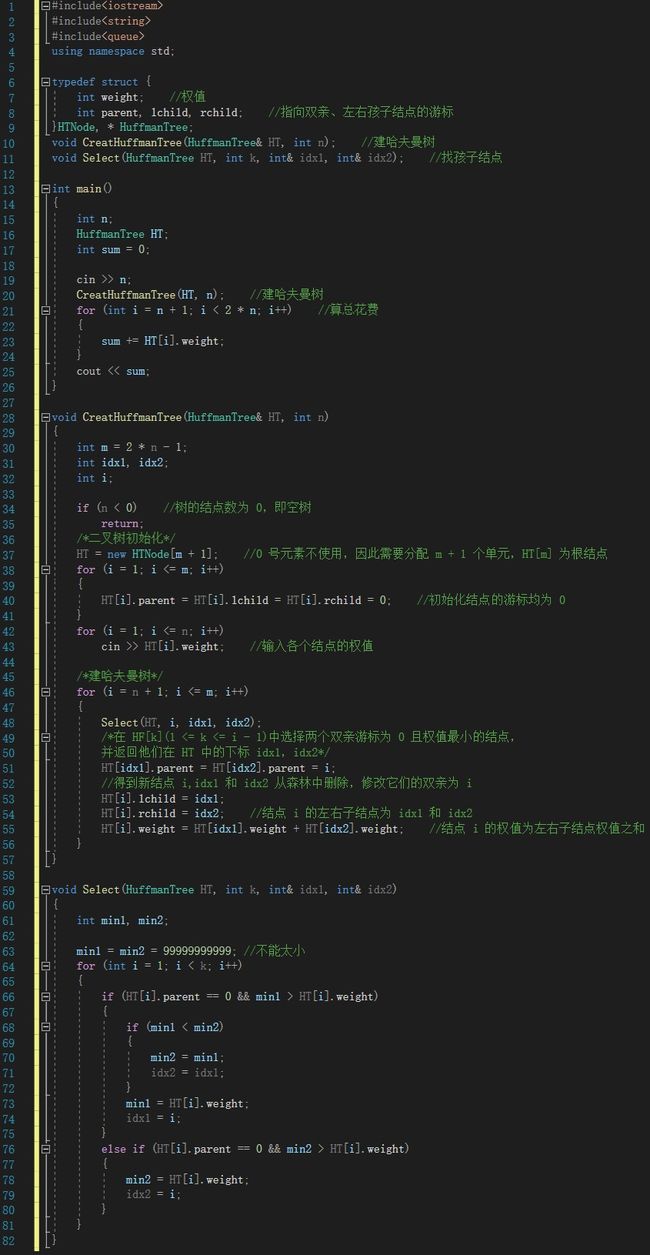
代码实现
void CreatHuffmanTree(HuffmanTree &HT,int n)
{
int m = 2 * n - 1;
int idx1,idx2;
int i;
if(n < 0) //树的结点数为 0,即空树
return;
/*二叉树初始化*/
HT = new HTNode[m + 1]; //0 号元素不使用,因此需要分配 m + 1 个单元,HT[m] 为根结点
for(i = 1; i <= m; i++)
{
HT[i].parent = HT[i].lchild = HT[i].rchild = 0; //初始化结点的游标均为 0
}
for(i = 1; i <= n; i++)
cin >> HT[i].weight; //输入各个结点的权值
/*建哈夫曼树*/
for(i = n + 1; i <= m; i++)
{
Select(HT,i - 1,idx1,idx2);
/*在 HF[k](1 <= k <= i - 1)中选择两个双亲游标为 0 且权值最小的结点,
并返回他们在 HT 中的下标 idx1,idx2*/
HT[idx1].parent = HT[idx2].parent = i;
//得到新结点 i,idx1 和 idx2 从森林中删除,修改它们的双亲为 i
HT[i].lchild = idx1;
HT[i].rchild = idx2; //结点 i 的左右子结点为 idx1 和 idx2
HT[i].weight = HT[idx1].weight + HT[idx2].weight; //结点 i 的权值为左右子结点权值之和
}
}
Select 函数样例
void Select(HuffmanTree HT, int k, int& idx1, int& idx2)
{ //在 HF[k](1 <= k <= i - 1)中选择两个双亲游标为 0 且权值最小的结点,
int min1, min2; //并返回他们在 HT 中的下标 idx1,idx2
min1 = min2 = 999999;
for (int i = 1; i < k; i++)
{
if (HT[i].parent == 0 && min1 > HT[i].weight)
{
if (min1 < min2)
{
min2 = min1;
idx2 = idx1;
}
min1 = HT[i].weight;
idx1 = i;
}
else if (HT[i].parent == 0 && min2 > HT[i].weight)
{
min2 = HT[i].weight;
idx2 = i;
}
}
}
根据哈夫曼树求哈夫曼编码
算法解析
在拥有哈夫曼对应的哈夫曼树的时候,求哈夫曼编码的思想是:依次从叶结点向上回溯至根结点,回溯时走左分支生成编码 0,走右分支生成编码 1。根据这个思想,对于每个字符得到的编码顺序是从右向左的,因此存储编码的数据结构的逻辑顺序应道从后往前。我们可以用顺序表来存储哈夫曼编码表,为了方便操作,我们使用数组来实现,数组的 0 号单元不使用。由于每个字符的编码的具体长度不能被确定,但是字符编码长度一定小于哈夫曼编码的长度,因此可以分配以该长度作为数组上限的一维数组来存储。
代码实现
typedef char **HuffmanCode; //哈弗曼编码表存储结构
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC, int n)
{
int start;
int c,f;
HC = new char *[n + 1]; //分配 n 个字符编码的空间,存储字符编码表
cd = new char [n]; //临时存储每个字符的编码的数组
cd[n - 1] = '/0'; //放置结束符
for(int i; i <= n; i++) //求所有字符的哈夫曼编码
{
start = n - 1; //start 为初始指向编码结束符的游标
c = i
f = HF[i].parent; //f 指向 c 结点的双亲
while(f != 0) //从叶结点向上回溯,直至根结点
{
--start; //回溯 start 前一个位置
if(HF[f].lchild == c) //判断 c 结点是 f 的哪个孩子
cd[start] = '0'; //左孩子,编码 0
else
cd[start] = '1'; //右孩子,编码 1
c = f;
f = HF[f].parent; //向上回溯
}
//到此,求出第 i 个字符编码
HC[i] = new char[n - start];
strcpy(HC[i],&cd[start]); //将编码拷贝
}
delete cd;
}
应用举例
修理牧场(哈夫曼树实现)
情景模拟
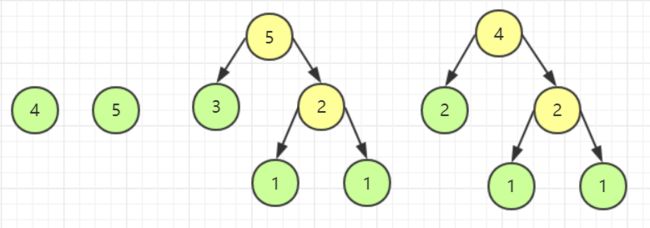
我们如果按照分割木块的思想去分析,会显得很不直观,所以我们直接通过我们的目标来组合出最花费的情况,那么这就很显然要使用贪心算法来解决。如图所示用圆形来表示小木块。

要保证花费更小,就需要让较短的木块后生成,较长的木块先生成,因此我选择较小的两个木块,还原为它们被分割出来之前的状态。即选择两个长度为 1 的木块,组合成一个长度为 2 的木块。

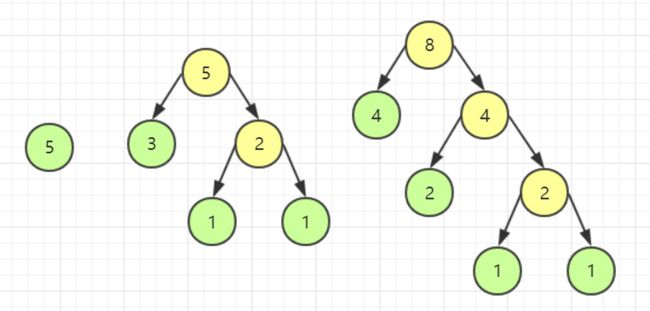
接下来我要去生成下一个木块,选择两个目前最短的木块,还是两个 1 长度的木块,组合成长度为 2 的木块。
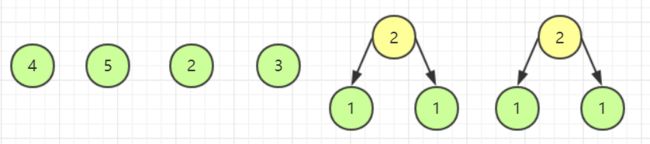
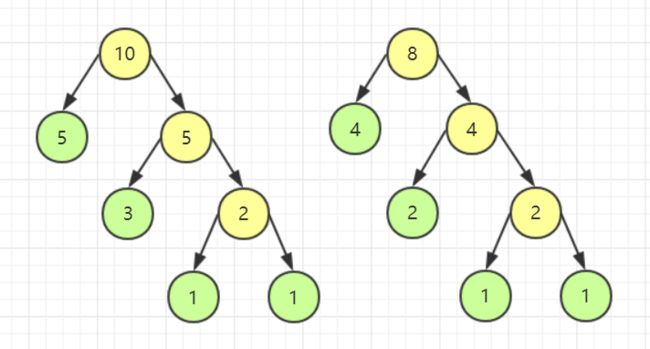
重复上述操作。
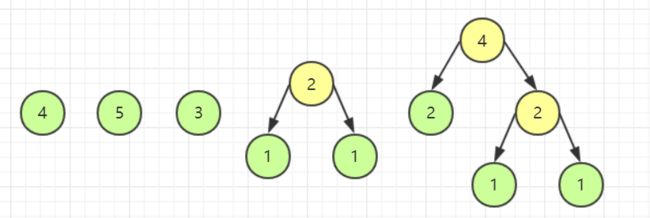
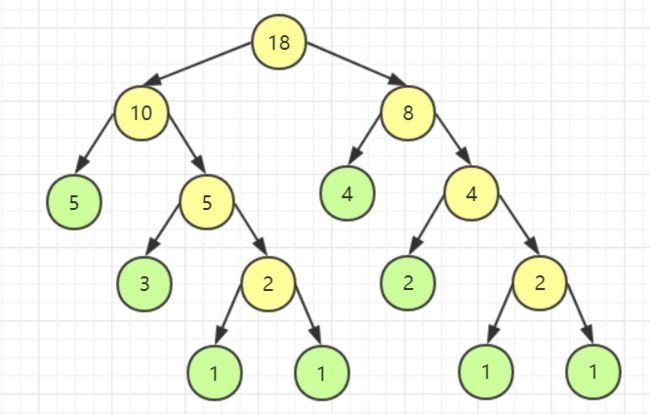
模拟完毕,观察一下我们发现,我们已经还原出了木块的每一次应该如何切割,由于木块切割费用与其长度相等,因此我们把黄色源泉的数字都加起来,发现正好是 49。此时我可以说,问题已经解决了,我们把目标木块当成一个个结点,长度当做权,这道题不就是要建一棵哈夫曼树嘛。
代码实现
参考资料
哈夫曼编码
《大话数据结构》—— 程杰 著,清华大学出版社
《数据结构教程》—— 李春葆 主编,清华大学出版社
《数据结构(C语言版|第二版)》—— 严蔚敏 李冬梅 吴伟民 编著,人民邮电出版社