今天要讲的三种排序算法的时间复杂度都是O(n),因为它们的时间复杂度是线性的,所以我们把这类排序算法叫做线性排序。之所以能够做到线性的时间复杂度,是因为这三个算法是非基于比较的排序算法,都不涉及元素之间的比较操作。但是它们对要排序的数据要求很苛刻,所以我们今天主要学习一下这些排序算法适用的场景。
1桶排序
桶排序的核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
分析一下桶排序的时间复杂度:如果要排序的数据有n个,我们把它们均匀地划分到m个桶内,每个桶里就有k=n/m个元素。每个桶内使用快速排序,时间复杂度为O(k*logk)。m个桶排序的时间复杂度就是O(m*k*logk),因为k=n/m,所以整个桶排序的时间复杂度就是O(n*log(n/m))。当桶的个数m接近数据个数n时,log(n/m)就是一个非常小的常量,这个时候桶排序的时间复杂度接近O(n)。
桶排序对数据的要求:
第一,要排序的数据需要很容易就能划分成m个桶,且桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完成之后,桶与桶之间无需再进行排序。
第二,数据在各个桶之间的分布要比较均匀。若不均匀,那桶内数据排序的时间复杂度就不是常量级了,在极端情况下,如果数据都被划分到一个桶里,那就退化为O(nlogn)的排序算法了。
桶排序比较适合用在外部排序中。所为外部排序,就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。我们就将数据划分成n个桶,然后将每个桶内的数据依次读取到内存中进行排序,所有桶都排序完成后,再将这n个文件依次写入到一个文件中就OK了。如果数据没有均匀分布,某个桶内的数据比较多也超过了内存的限制,我们可以对这个桶内的数据继续划分成更小的桶,如果划分之后数据量还是超过限制,那就继续再划分,直到所有的文件都能读入内存为止。
2计数排序
计数排序其实很像桶排序的一种特殊情况。当要排序的n个数据所处范围并不大的时候,比如最大值是k,我们就可以把数据划分成k个桶,每个桶内的数据都是相同的,省略掉了桶内排序的时间。所以计数排序的算法思想和桶时分类似,只是桶的大小粒度不一样。
但是它为什么叫计数排序呢?
计数的方法才是计数排序算法的精髓。
下面用一个例子来理解计数排序算法的精髓。
假设有8个考生,分数在0-5分之间,这8个考生的成绩我们放在一个数组A[8]中,它们分别是:2,5,3,0,2,3,0,3。
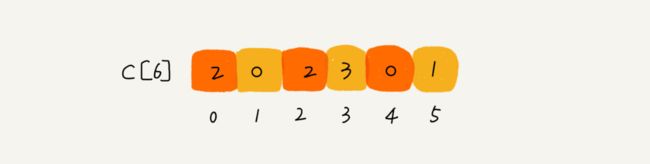
因为考生的成绩在0-5分之间,所以我们使用大小为6的数组C[6]表示桶,其中下标对应分数。不过,C[6]内存储的并不是考生,而是考生个数。我们只需要遍历一遍考生的分数,就可以得到C[6]的值:
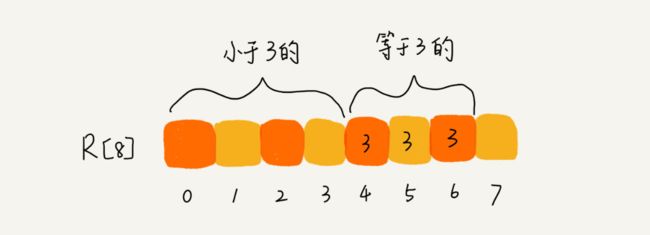
由上图可以看出,分数为3分的考生有3个,小于3分的考生有4个,所以成绩为3分的考生在排序之后的有序数组R[8]中,会保存在下标4,5,6的位置。
那我们该如何快速计算出每个分数的考生在有序数组中对应的存储位置呢?这个处理方式非常巧妙。
我们对C[6]数组顺序求和,C[6]存储的数据就变成了如下的样子:
其中,C[k]里存储的是小于等于分数k的考生个数。
接下来,我们从前到后扫描数组A({2,5,3,0,2,3,0,3}),比如当扫描到3时,我们可以从数组C中取出下表为3的值:7,这个7的含义是,包括扫描到的A中的这个3在内,分数小于等于3的考生有7个,也就是说3是数组R中的第7个元素(即数组R中下标为6的位置),当3放入到数组R中后,小于等于3的元素就只剩下6个了,所以相应C[3]要减1,变成6。以此类推,当我们扫描到第2个分数为3的考生的时候,就会把它放入数组R中的第6个元素的位置(即数组R中下标为5的位置)。当我们扫描完整个数组A之后,数组R内的数据就是按照分数从小到大有序排列的了。
过程如下图所示:
代码如下:
运行结果:
注意,计数排序只能用在数据范围不大的场景中,如果数据范围k比要排序的数据n大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转换为非负整数。比如数据是精确到小数点后一位,我们可以将所有数据都先乘10转换成整数,再分到相应个数的桶内,如果数据中有负数,比如范围是[-1000,1000],我们就需要先对每个数据都加1000,转化成非负整数。
戳这里查看源代码。
2基数排序
假设我们有10万个手机号码,希望将这10万个手机号码从小到大排序,每个手机号码11位,数据范围这么大,显然桶排序、计数排序的方法就不使用了~用快排的话时间复杂度可以做到O(nlogn),还有更高效的算法吗?
记下来介绍的排序算法就可以用O(n)的时间复杂度解决这个问题,它就是基数排序。
基数排序的实现思路是,先按照最后一位来排序手机号码,然后再按照倒数第二位排序重新排序,以此类推,最后按照第一位重新排序,经过11次排序之后,手机号码就都有序了。
注意:这按照每位来排序的排序算法要是稳定的,否则这个实现思路就是不正确的。
根据每一位来排序,我们可以用刚刚讲过的桶排序或者计数排序,它们的时间复杂度可以做到O(n),如果要排序的数据有k位,那我们就需要k次桶排序或者计数排序,总的时间复杂度是O(k*n)。当k不大的时候,比如在这个例子中,k最大就是11,所以基数排序的时间复杂度就近似于O(n)。
有时候要排序的数据并不都是等长的,这个时候我们可以把所有数据都补齐到相同长度,位数不够的可以在后面补“0”,因为根据ASCII值,所有字母都大于“0”,所以补“0”不会影响到原有的大小顺序,这样就可以继续使用基数排序了。
总结一下,基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系,如果a数据的高位比b数据大,那剩下的低位就不用比较了,除此之外,每一位数据的范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到O(n)了。
3内容小结
今天我们学习了3种线性时间复杂度的排序算法,有桶排序、计数排序、基数排序,它们对要排序的数据都有比较苛刻的要求,应用不是非常广泛。但是如果数据特征比较符合这些排序算法的要求,应用这些排序算法会非常高效,线性时间复杂度可以达到O(n)。
桶排序和计数排序的思想非常相似,都是针对范围不大的数据,将数据划分成不同的桶来实现排序。基数排序要求数据可以划分成高低位,位之间有递进关系。比较两个数,我们只需要比较高位,高位相同的再比较低位。而且每一位的数据范围不能太大,因为基数排序算法需要借助桶排序或者计数排序来完成每一个位的排序工作。