Image by pangziai on Pixabay
今天是一年一度的植树节,说到树,我就想到了《西游记》中的古树精,今年下半年。。。好了好了,不皮了,我们直接开花。今天就趁着植树节来种一棵我们程序员的“树”吧。
什么是“树”?
在种树之前,我们先来了解下什么是树?看个例子:
不对不对,放错了,应该是下面这个:
维基百科对于树的定义是:
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
说白了,只要是形如上图的数据结构就叫树。
二叉树
自然界中有“迎客松”、“轩辕柏”这样出名的树,我们今天要种的树也是我们IT圈里面的扛把子——“二叉树”。
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构之一。
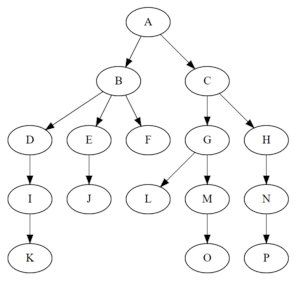
二叉树的特点是每个结点最多有两个子树,左边的叫做左子树,右边的叫做右子树,二叉树要么为空,要么由根结点、左子树和右子树组成,而左子树和右子树分别是一棵二叉树。 下面这棵树就是一棵二叉树。
常见术语
- 结点(node):上图中的 A、B、C。。。就是一个结点
- 结点的度:一个结点含有的子树的个数称为该结点的度
- 树的度:一棵树中,最大的结点的度称为树的度
- 深度:对于任意节点 n , n 的深度为从根到 n 的唯一路径长,根的深度为 0;
- 高度:对于任意节点 n , n 的高度为从 n 到一片树叶的最长路径长,所有树叶的高度为 0;
种树
接下来的代码均用 Java 展现,完整代码可在公众号「01二进制」后台回复“二叉树”查看。
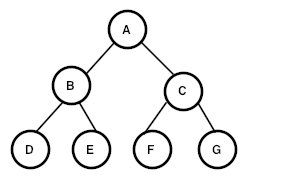
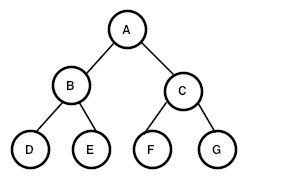
现在我们就开始种一棵如上图的树吧。根据定义,我们了解到,结点是一棵二叉树最重要的元素,而作为一个结点,必须满足以下条件:
- 根结点
- 左子树和右子树
因此我们可以创建一个结点类(TreeNode):
class TreeNode {
String data;
TreeNode left;
TreeNode right;
TreeNode(String data) {
this.data = data;
}
}
有了这个结点类之后我们就可以创建出一个如上图的树了:
// 创建二叉树
private TreeNode createTree() {
TreeNode root = new TreeNode("A");
root.left = new TreeNode("B");
root.right = new TreeNode("C");
root.left.left = new TreeNode("D");
root.left.right = new TreeNode("E");
root.right.left = new TreeNode("F");
root.right.right = new TreeNode("G");
return root;
}
你看,一棵树不就种好了吗?
树的特征
作为一个新时代的好青年,我们不能把树种好了就不管不顾了,得负起责任啊。最起码你要知道自己的树长啥样吧。所以接下来我们就来看看如何获取树的特征。
我们描述一个人的特征往往都是从他的外形、长相、身材入手的,描述一颗树也是如此,我们接下来将会从下面几个角度去获取树的特征:
- 判断是否为空
- 获取树的高度
- 获取树中的结点个数
判断是否为空
// 判断是否为空
public boolean isEmpty(TreeNode root) {
return root == null;
}
获取树的高度
这里我们采用递归的方式,因为树的高度是由其子树决定的,所以我们只需要比较左、右子树的高度然后取最大值即可,代码如下:
// 获取树的高度
private int height(TreeNode root) {
if (root == null)
return 0;//递归结束:空树高度为0
else {
int i = height(root.left);
int j = height(root.right);
return (i < j) ? (j + 1) : (i + 1);
}
}
获取树的结点大小(个数)
一个树的结点个数必定为其左子树的结点个数 + 右子树的结点个数 +1,因此我们同样可以用递归非常简单的将其表示出来:
// 获取结点大小
private int size(TreeNode root) {
if (root == null) {
return 0;
} else {
return 1 + size(root.left) + size(root.right);
}
}
遍历二叉树
上一节中我们获取到了树的特征,但这远远不够,特征只能粗略的描述一个二叉树,想要详细的了解一个二叉树,我们必须对其进行“遍历”。
遍历二叉树是指以一定的次序访问二叉树中的每个结点。所谓访问结点是指对结点进行各种操作的简称(最简单的就是访问该结点的值)。
而访问结点无非就 3 个操作:
- 访问结点本身(N)
- 访问左结点(L)
- 访问右结点(R)
我们以根结点为核心,如果先访问根节点在访问左右结点成为前序遍历;如果先访问左结点然后根结点最后右结点则为中序遍历;若最后访问根节点则为后序遍历。
因此上图的遍历结果为:
前序:A B D E C F G
中序:D B E A F C G
后序:D E B F G C A
当然这只是我们自己根据定义手写出来的,该如何用代码表示出来呢?
前序遍历
根据定义我们知道,前序遍历就是先访问根结点,然后是左结点和右结点,因此用递归可以很简单的展现这一过程:
// 前序遍历二叉树
private void preOrder(TreeNode root) {
if (root != null) {
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
}
中序遍历
同理我们也可以很快的知道中序和后序遍历了:
// 中序遍历二叉树
private void inOrder(TreeNode root) {
if (root != null) {
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
}
后序遍历
// 后序遍历二叉树
private void postOrder(TreeNode root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
}
这里遍历二叉树的代码均是以递归方法完成的,非递归遍历二叉树的过程较为麻烦,由于篇幅限制,这里就不放出来了。若想查看非递归版本的代码可在公众号「01二进制」后台回复“二叉树”查看。
层序遍历
事实上,以人来看一个树的话大多都是一层一层的看,这种遍历方式称为层序遍历。具体思路:用队列实现,先将根节点入队列,只要队列不为空,然后出队列,并访问,接着讲访问节点的左右子树依次入队列。
// 层序遍历
private void levelTravel(TreeNode root) {
if (root == null) return;
Queue q = new LinkedList();
q.add(root);
while (!q.isEmpty()) {
TreeNode temp = q.poll();
System.out.print(temp.data + " ");
if (temp.left != null) q.add(temp.left);
if (temp.right != null) q.add(temp.right);
}
}
扩展
二叉树的作用
二叉树是种非常强大的数据结构,那她到底强大在哪里呢?我们来看下面这个简单的例子:
该例来自于Aditya Bhargava 的《算法图解》
假如说,你想从微博中找到一个人,最快的方法一般是二分查找。但当有新用户增加时,都得将新用户插入组别内再排序,因为二分查找法只会有序的组别才有用。
所以就有人想了,如果可以将新增的用户插入到数组的正确位置就好了,这样就不需要在插入后在排序了。
于是就有人设计了一种二叉树:对于每个结点,左子节点的值都比它小,右子节点值都比它大。如下图所示:
Maggie排在David后面,因此向右找Maggie,排在Manning前面,因此向左找。
这个运行时间,用大O表示法,平均运行时间是O(log2 N),最差运行时间是O(N)
在有序数组查找时,与二分查找法运行时间相同。
二叉树对比二分查找法优势在于<如下图>:
可以看出插入和删除速度都快。二叉树的缺点也很明显,就是不能随机访问。
二叉树的扩展
上述例子其实就是一个二叉查找树的简易使用,那么除此之外二叉树还有什么常见的应用呢?下面列出四个,有兴趣的小伙伴可以自己搜索相关的文档阅读学习。
- B- 树,是一种特殊的二叉树,数据库常用它来存储数据。
- B+ 树,B+树是 B-树的一种变体,主要用于磁盘文件组织、数据索引和数据库索引等场景。
- 红黑树,二叉平衡树的一种,Java 中的 TreeSet ,TreeMap,HashMap就是这种数据结构。
- 堆,是一种完全二叉树,可以实现优先队列。
END
种一棵树最好的时间是十年前,而后是现在。我们常常去后悔过去的事情。遗憾自己犯的错误,遗憾自己错过的机会。虽然现实很让人感到可惜,但其实很多事情早就该做了,再懊恼又有什么用呢?与其无端抱怨还不如行动起来。当你感到遗憾时,才是行动的最好时机!
“关注我最好的时间是3分钟前,而后是现在”