问题引申
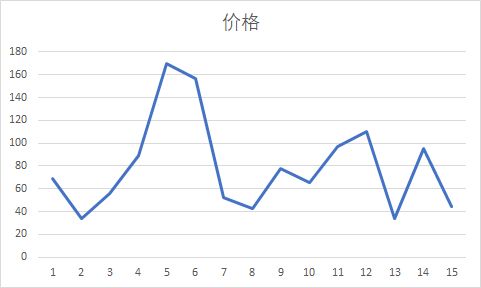
假如下面是一家公司股票的价格变动情况,现在你要确定在哪天买入,哪天抛出才能实现利益最大化
暴力求解法
尝试求出每对可能的买进和卖出的日期组合,只要卖出日期在买入日期之后即可。
这样,可以利用排列组合求得共有n(n-1)/2种情况,对这些情况进行比较,可以求得最大子数组
问题变换
我们的目的是寻找一段日期,使得从第一天到最后一天的股票净增长最大。我们可以不再从每日价格的角度去看待数据,而是考查每日价格变化,第i天的价格变化定义为第i天与第i-1天的价格差。
如果将这些价格差看做一个数组A,那么问题就转化为寻找A的和为最大的连续非空子数组。称这样的子数组为最大子数组。
使用分治策略的求解方法
在数组A[low...high]中,任何连续子数组所处的位置必定是以下三种情况之一:
- 完全位于A[low...mid]中
- 完全位于A[mid+1...high]中
- 跨越了中点
可以在线性时间内求得跨越中点的最大子数组
跨越中点的最大子数组
private static int[] find_maximum_subarray(int[] A, int low, int high){
int[] result = new int[3]; //存放结果的数组
int[] left_result; //存放左子数组的最大子数组
int[] right_result; //存放右子数组的最大子数组
int[] cross_result; //存放跨越中点的最大子数组
if (low == high){ //数组中只有一个元素的情况,直接返回
result[0] = low;
result[1] = high;
result[2] = A[low];
return result;
}else {
int mid = (low+high)/2;
left_result = find_maximum_subarray(A, low, mid); //递归求左子数组的最大子数组
right_result = find_maximum_subarray(A, mid+1, high); //递归求右子数组的最大子数组
//求本层中跨越中点的最大子数组,从此行开始进行合并工作
cross_result = find_max_crossing_subarray(A, low, mid, high);
if (left_result[2] >= right_result[2] && left_result[2] >= cross_result[2]){
return left_result;
}else if (right_result[2] >= left_result[2] && right_result[2] >= cross_result[2] ){
return right_result;
}else {
return cross_result;
}
}
}
分治法求解
有了可以在线性时间内求得跨越中点的最大子数组的算法,就可以设计出求解最大子数组的分治算法了
伪代码:
java实现
public class Maximum_subarray{
public static void main(String[] args) {
int[] arr = {-29,5,-2,7,9,6,3,-98,12,45,-18,87,-546};
int[] a = find_maximum_subarray(arr, 0, 12);
for(int i:a){
System.out.println(i);
}
}
//寻找跨越中点的最大子数组方法
private static int[] find_max_crossing_subarray(int[] A,int low,int mid,int high){
int left_sum = -999;
int right_sum = -999;
int left = 0;
int right = 0;
int sum = 0;
for(int i=mid;i >= low;i--){
sum = sum+A[i];
if(sum > left_sum){
left_sum = sum;
left = i;
}
}
sum = 0;
for(int j = mid+1;j <= high;j++){
sum = sum + A[j];
if(sum > right_sum){
right_sum = sum;
right = j;
}
}
int[] result = {left, right, left_sum+right_sum};
return result;
}
private static int[] find_maximum_subarray(int[] A, int low, int high){
int[] result = new int[3]; //存放结果的数组
int[] left_result; //存放左子数组的最大子数组
int[] right_result; //存放右子数组的最大子数组
int[] cross_result; //存放跨越中点的最大子数组
if (low == high){ //数组中只有一个元素的情况,直接返回
result[0] = low;
result[1] = high;
result[2] = A[low];
return result;
}else {
int mid = (low+high)/2;
left_result = find_maximum_subarray(A, low, mid); //递归求左子数组的最大子数组
right_result = find_maximum_subarray(A, mid+1, high); //递归求右子数组的最大子数组
//求本层中跨越中点的最大子数组,从此行开始进行合并工作
cross_result = find_max_crossing_subarray(A, low, mid, high);
if (left_result[2] >= right_result[2] && left_result[2] >= cross_result[2]){
return left_result;
}else if (right_result[2] >= left_result[2] && right_result[2] >= cross_result[2] ){
return right_result;
}else {
return cross_result;
}
}
}
}