公共子序列与公共子串问题

1、公共子序列问题

网上有很多关于公共子序列问题，说的大同小异，看了很多不明白，很多都是晦涩难懂，这里分享一个连接，个人觉得讲述的比较明白，易懂。

http://blog.csdn.net/v_july_v/article/details/6695482

我这里也简单的把自己的理解说一下，求公共子序列问题是一个非常常见的问题，最差的方法就是暴力匹配，暴力匹配算法第一步求去短字符串的所有序列组合，然后从长到短一个一个的去匹配时候有公共序列相同，即使使用了这样的剪枝，该算法效率任然很低。

比较受人青睐的算法当然莫过于动态规划了，动态规划的核心是找到转移方程。把复杂的问题通过转移方程转移到子问题。

• 动态规划算法

    事实上，最长公共子序列问题也有最优子结构性质。

记:

Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

• 若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

• 若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

    由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

所以解决这个问题的动态转移方程即：

if xm==yn  LCS(Xm,Yn)= LCS（Xm-1，Yn-1）+1;
if xm!=yn LCS(Xm,Yn)=  max{LCS（Xm-1，Yn),LCS（Xm，Yn-1)};

代码如下：

#include <stdio.h>

#include <string.h>



/*

c[i][j]存储的是字串1到i位置，字串2到j位置时公共子序列的最大长度



if str1[i] == str2[j]    c[i][j] = c[i-1][j-1]+1;

if str1[i] != str2[j]    c[i][j] = max{c[i-1][j],c[i][j-1]}

*/

int lcs(char *str1,char *str2,int len1,int len2,int c[100][100])

{

    if (str1 == NULL || str2 ==NULL)

    {

        return -1;//输入字符串错误

    }

    //初始化记录dp的二维数组

    for (int i = 0; i <= len1; i++)

    {

        for (int j = 0; j <= len2; j++)

        {

            c[i][j] = 0;

        }

    }

    //dp运算

    for (int i = 1; i <= len1; i++)

    {

        for (int j = 1; j <= len2; j++)

        {

            if(str1[i-1] == str2[j-1])

            {

                c[i][j]=c[i-1][j-1]+1;

            }

            else {

                c[i][j] = c[i-1][j]>c[i][j-1]?c[i-1][j]:c[i][j-1];

            }

        }

    }

    //打印出dp数组存储的内容

    for (int i = 0; i <= len1; i++)

    {

        for (int j = 0; j <= len2; j++)

        {

            printf("%d ",c[i][j]);

        }

        printf("\n");

    }



    //打印出公共子序列

    char str[100]={0};

    int index = c[len1][len2]-1;

    for (int i = len1,j = len2; i>0&&j>0;)

    {

        if(str1[i-1] == str2[j-1])

        {

            str[index--] = str1[i-1];

            i--;

            j--;

        }

        else 

        {

            if(c[i][j-1]>c[i-1][j])

            {

                j--;

            }else 

            {

                i--;

            }

        }

    }

    printf("公共子序列为：%s\n",str);

    return c[len1][len2];

}





int main(int argc, char **argv)

{

    char str1[] = {"ABCBDAB"};

    char str2[] = {"BDCABA"};

    int c[100][100];

    int len1 = strlen(str1);

    int len2 = strlen(str2);

    int num = lcs(str1,str2,len1,len2,c);

    printf("公共子序列的长度：%d\n",num);

    return 0;

}

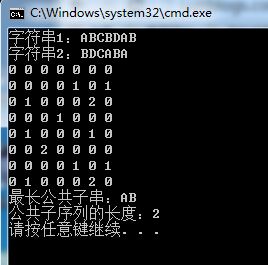
 运行结果

 

2、最大公共子串

首先区分下公共字串和公共子序列的区别，公共子序列是在整个字符串中只要按照顺序可以不用连续的，但是公共子串是指必须连续的字符串，举个例子

 

ABCBDAB

BDCABA

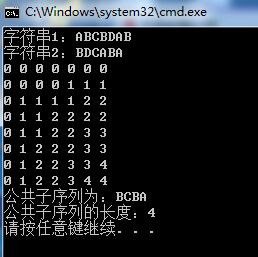
公共子序列是  BCBA

公共字串是  AB

求公共字串比公共子序列稍微简单了一些，如果上边所述，公共子串也可以用暴力匹配方法，求出较短的字符串的所有子串，然后可以从长到短利用kmp字符串匹配算法求出公共子串，同时还添加了剪枝，但是字样的暴力匹配效率始终是比较差的，最好的方法还是使用动态规划。

根据上边公共子序列动态规划的方法分析，其实我们可以发现公共子串和公共子序列非常类似

只是在状态转移方程是稍有不同，

   事实上，最长公共子串问题也有最优子结构性质。

记:

Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

• 若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子串Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子串。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

• 重要的是这里的不同：

  • 若xm≠yn，由于zk≠xm与zk≠yn 那么说明之前相同的字符串也不能连接起来，此时的LCS(X,Y) 的长度回归到0重新找最长的公共子串。

所以：关于最长公共子串的动态转移方程为：

if xm==yn  LCS(Xm,Yn)= LCS（Xm-1，Yn-1）+1;
if xm!=yn LCS(Xm,Yn)=  0;

代码如下：

#include <stdio.h>

#include <string.h>



/*

c[i][j]存储的是字串1到i位置，字串2到j位置时公共字串的最大长度



if str1[i] == str2[j]    c[i][j] = c[i-1][j-1]+1;

if str1[i] != str2[j]    c[i][j] = 0

*/

int lcs(char *str1,char *str2,int len1,int len2,int c[100][100])

{

    if (str1 == NULL || str2 ==NULL)

    {

        return -1;//输入字符串错误

    }

    //初始化记录dp的二维数组

    for (int i = 0; i <= len1; i++)

    {

        for (int j = 0; j <= len2; j++)

        {

            c[i][j] = 0;

        }

    }

    //dp运算

    int max = -1;

    int col=0,row=0;

    for (int i = 1; i <= len1; i++)

    {

        for (int j = 1; j <= len2; j++)

        {

            if(str1[i-1] == str2[j-1])

            {

                c[i][j]=c[i-1][j-1]+1;

                if(c[i][j]>max)

                {

                    row = i;

                    col = j;

                    max = c[i][j];

                }

            }

            else {

                c[i][j] = 0;

            }

        }

    }

    //打印出dp数组存储的内容

    for (int i = 0; i <= len1; i++)

    {

        for (int j = 0; j <= len2; j++)

        {

            printf("%d ",c[i][j]);

        }

        printf("\n");

    }

    

    //打印出公共子串

    printf("最长公共子串：");

    for (int i = row-max; i<row;i++)

    {

        printf("%c",str1[i]);

    }

    printf("\n");

    return max;

}





int main(int argc, char **argv)

{

    char str1[] = {"ABCBDAB"};

    char str2[] = {"BDCABA"};

    int c[100][100];

    int len1 = strlen(str1);

    int len2 = strlen(str2);

    printf("字符串1：%s\n",str1);

    printf("字符串2：%s\n",str2);

    int num = lcs(str1,str2,len1,len2,c);

    printf("公共子序列的长度：%d\n",num);

    return 0;

}

结果：