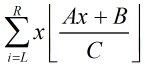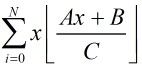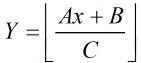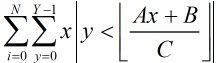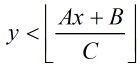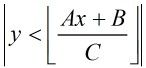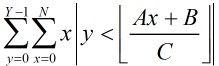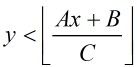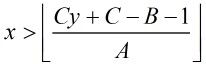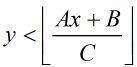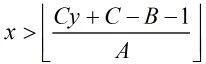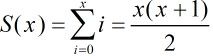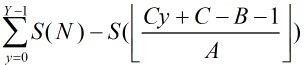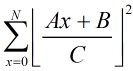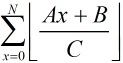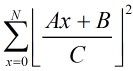BZOJ2831(小强的金字塔系列问题--区域整点数求法)

题目：2831: 小强的金字塔

题意就是给出A,B,C,R,L，然后求

这里其实用到扩展欧几里德。(基本上参照clj的解题报告才理解的)

分析：我们先来分析一般情况：

这里我们假设A<C和B<C，否则我们可以把它化成A<C,B<C的情况

我们令：，所以上式就等价于：

，如果，那么的值是1，否则为0

然后我们交换顺序：，由于，所以

推导过程：因为，所以，那么，进一步有：

，所以

令：

那么式子就转化为：

这样一看我们就交换了A，C了，也就是扩展欧几里德算法，详见金斌2009论文。

我们继续化简，发现又把问题转化成求： 和 

这样的话与上面同样的思路继续化简：对于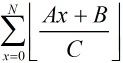比较简单，就不写过程了。

下面来说说的化简过程：

然后分析就完毕！

由于本题的数很大，要用高精度，用Python最好，因为一是Python高精度可以直接算，二是Python直接返回元组方便。

 

sum = lambda n : n*(n+1)/2
sqrtsum = lambda n : n*(n+1)*(2*n+1)/6

def f(a,b,c,r):
     if r<0:
         return [0]*3

     if a>=c:
         t=f(a%c,b,c,r)
         a/=c
         return [t[0]+a*sqrtsum(r),t[1]+a*sum(r),t[2]+a*a*sqrtsum(r)+2*a*t[0]]

     elif b>=c:
          t=f(a,b%c,c,r)
          b/=c
          return [t[0]+b*sum(r),t[1]+b*(r+1),t[2]+b*b*(r+1)+2*b*t[1]]

     else:
          if a==0:
              return [0]*3
          y=(a*r+b)/c
          t=f(c,c-b-1,a,y-1)
          ans=[y*sum(r)-(t[1]+t[2])/2,y*r-t[1],y*y*r-2*t[0]-t[1]]
          return ans


a,c,b,l,r=map(int,raw_input().split())
print f(a,b,c,r)[0]-f(a,b,c,l-1)[0]

 

典型题目一：SPOJ4717. Grid Points in a Triangle

题意：求满足 y <= ax / b and x <= n的整点个数，x,y,a,b,n都是非负的整数。

分析：实际上就是求：，就是上题的思路。

 

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;
typedef long long LL;

LL gcd(LL a,LL b)
{
    return b? gcd(b,a%b):a;
}

LL dfs(LL n,LL a,LL b)
{
    LL t=n*(n+1)/2*(a/b);
    a%=b;
    if(a==0) return n+1+t;
    LL d=a*n/b;
    t+=(n+1)*(d+1)+d/a+1;
    return t-dfs(d,b,a);
}

int main()
{
    LL t,n,a,b,p;
    scanf("%lld",&t);
    while(t--)
    {
        scanf("%lld%lld%lld",&n,&a,&b);
        p=gcd(a,b);
        printf("%lld\n",dfs(n,a/p,b/p));
    }
    return 0;
}

 

典型题目二：2013年ACM全国邀请赛南京赛区一题：http://icpc.njust.edu.cn/Local/1742

分析：本题比较难，其实方法跟上题差不多，要分析的过程更加复杂些。