线性规划 整数规划 01规划
在数学中,线性规划(Linear Programming,简称LP)问题是目标函数和约束条件都是线性的最优化问题。
线性规划是最优化问题中的重要领域之一。很多运筹学中的实际问题都可以用线性规划来表述。线性规划的某些特殊情况,例如网络流、多商品流量等问题,都被认为非常重要,并有大量对其算法的专门研究。很多其他种类的最优化问题算法都可以分拆成线性规划子问题,然后求得解。在历史上,由线性规划引申出的很多概念,启发了最优化理论的核心概念,诸如“对偶”、“分解”、“凸性”的重要性及其一般化等。同样的,在微观经济学和商业管理领域,线性规划被大量应用于解决收入极大化或生产过程的成本极小化之类的问题。乔治·丹齐格被认为是线性规划之父。
目录
[隐藏]- 1 标准型
- 1.1 例子
- 2 增广矩阵(松弛型)
- 2.1 例子
- 3 对偶
- 3.1 例子
- 4 理论
- 5 算法
- 6 整数规划
- 7 参见
- 8 参考
- 9 外部链接
标准型[编辑]
描述线性规划问题的常用和最直观形式是标准型。标准型包括以下三个部分:
- 一个需要极大化的线性函数,例如
- 以下形式的问题约束,例如:
- 和非负变量,例如:
线性规划问题通常可以用矩阵形式表达成:
-
maximize
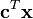
-
subject to

其他类型的问题,例如极小化问题,不同形式的约束问题,和有负变量的问题,都可以改写成其等价问题的标准型。
例子[编辑]
以下是一个线性规划的例子。假设一个农夫有一块A平方千米的农地,打算种植小麦或大麦,或是两者依某一比例混合种植。该农夫只可以使用有限数量的肥料F和农药P,而单位面积的小麦和大麦都需要不同数量的肥料和农药,小麦以(F1, P1)表示,大麦以(F2, P2)表示。设小麦和大麦的售出价格分别为S1和 S2,则小麦与大麦的种植面积问题可以表示为以下的线性规划问题:
| max |
(最大化利润 - 目标函数) | |
| s.t. | (种植面积的限制) | |
| (肥料数量的限制) | ||
| (农药数量的限制) | ||
| (不可以栽种负数的面积) | ||
增广矩阵(松弛型)[编辑]
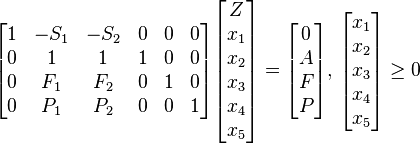
在用单纯型法求解线性规划问题之前,必须先把线性规划问题转换成增广矩阵形式。增广矩阵形式引入非负松弛变量将不等式约束变成等式约束。问题就可以写成以下形式:
这里xs是新引入的松弛变量, Z需要极大化的变量。
例子[编辑]
以上例子的转换成增广矩阵:
| maximize |
(目标函数) | |
| subject to | (augmented constraint) | |
| (augmented constraint) | ||
| (augmented constraint) | ||
这里![]() ,是(非负)松弛变量。
,是(非负)松弛变量。
写成矩阵形式:
对偶[编辑]
每个线性规划问题,称为原问题,都可以变换为一个对偶问题。我们可将“原问题”表达成矩阵形式:
-
maximize
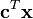
-
subject to

而相应的对偶问题就可以表达成以下矩阵形式:
-
minimize

-
subject to

这里用“y”来作为未知向量。
例子[编辑]
上述线性规划例子的对偶问题:
假如有一个种植园主缺少肥料和农药,他希望同这个农夫谈判付给农夫肥料和农药的价格。可以构造一个数学模型来研究如何既使得农夫觉得有利可图肯把肥料和农药的资源卖给他,又使得自己支付的金额最少?
问题可以表述如下
假设y1, y2分别表示每单位肥料和农药的价格,则所支付租金最小的目标函数可以表示为
| min |
|
| s.t. | |
| (控制购买价格使得农夫觉得有利可图) | |
| (同上) | |
| (不可以购买负数单位资源) | |
理论[编辑]
几何上,线性约束条件的集合相当于一个凸包或凸集,叫做可行域。因为目标函数亦是线性的,所以其极值点会自动成为最值点。线性目标函数亦暗示其最优解只会出现在其可行域的边界点中。
在两种情况下线性规划问题没有最优解。其中一种是在约束条件相互矛盾的情况下(例如x ≥ 2和x ≤ 1),其可行域将会变成空集,问题没有解,因此亦没有最优解。在这种情况下,该线性规划问题会被称之为“不可行”。
另一种情况是,约束条件的多面体可以在目标函数的方向无界(例如:max z=x1 + 3 x2 s.t. x1 ≥ 0, x2 ≥ 0, x1 + x2 ≥ 10),目标函数可以取得任意大的数值,所以没有最优解。
除了以上两种病态的情况以外(问题通常都会受到资源的限制,如上面的例子),最优解永远都能够在多面体的顶点中取得。但最优解未必是唯一的:有可能出现一组最优解,覆盖多面体的一条边、一个面、甚至是整个多面体(最后一种情况会在目标函数只能等于0的情况下出现)。
算法[编辑]
单纯形算法利用多面体的顶点构造一个可能的解,然后沿着多面体的边走到目标函数值更高的另一个顶点,直至到达最优解为止。虽然这个算法在实际上很有效率,在小心处理可能出现的“循环”的情况下,可以保证找到最优解,但它的最坏情况可以很坏:可以构筑一个线性规划问题,单纯形算法需要问题大小的指数倍的运行时间才能将之解出。事实上,有一段时期内人们曾不能确定线性规划问题是NP完全问题还是可以在多项式时间里解出的问题。
第一个在最坏情况具有多项式时间复杂度的线性规划算法在1979年由前苏联数学家Leonid Khachiyan提出。这个算法建基于非线性规划中Naum Shor发明的椭球法(ellip-soid method),该法又是Arkadi Nemirovski(2003年冯‧诺伊曼运筹学理论奖得主)和 D. Yudin的凸集最优化椭球法的一般化。
理论上,“椭球法”在最恶劣的情况下所需要的计算量要比“单形法”增长的缓慢,有希望用之解决超大型线性规划问题。但在实际应用上,Khachiyan的算法令人失望:一般来说,单纯形算法比它更有效率。它的重要性在于鼓励了对内点算法的研究。内点算法是针对单形法的“边界趋近”观念而改采“内部逼近”的路线,相对于只沿着可行域的边沿进行移动的单纯形算法,内点算法能够在可行域内移动。
1984年,贝尔实验室印度裔数学家卡马卡(Narendra Karmarkar)提出了投影尺度法(又名Karmarkar's algorithm)。这是第一个在理论上和实际上都表现良好的算法:它的最坏情况仅为多项式时间,且在实际问题中它比单纯形算法有显著的效率提升。自此之后,很多内点算法被提出来并进行分析。一个常见的内点算法为Mehrotra predictor-corrector method。尽管在理论上对它所知甚少,在实际应用中它却表现出色。
单形法沿着边界由一个顶点移动到“相邻”的顶点,内点算法每一步的移动考量较周详,“跨过可行解集合的内部”去逼近最佳解。当今的观点是:对于线性规划的日常应用问题而言,如果算法的实现良好,基于单纯形法和内点法的算法之间的效率没有太大差别,只有在超大型线性规划中,顶点几成天文数字,内点法有机会领先单形法。
线性规划的求解程式在各种各样的工业最优化问题里被广泛使用,例如运输网络的流量的最优化问题,其中很多都可以不太困难地被转换成线性规划问题。
线性规划理论中存在几个尚未解决的问题,这些开放问题的答案将会是数学运算中的根本突破,并且很可能是我们解决大规模线性规划问题的主要进展。
- LP存在强多项式时间算法吗?
- LP存在多项式时间算法以得到一个严格互补解吗?
- LP在实数(单位成本)模型下存在多项式时间算法吗?
这些问题已经由Stephen Smale在二十一世纪十八个尚未解决的最伟大的问题中应用。用Smale的话来说,“第三个问题是线性规划理论中最主要的尚未解决的问题”。然而,对于线性规划问题存在弱多项式时间算法,比如椭球算法和内点算法,尚未发现限制在约束条件个数和变量个数的强多项式时间算法,此算法的发展将会带来理论上重大意义,或者是解决大规模线性规划上的实际收益。
尽管赫尔希博士猜想近来被证明是错误的,但是它依旧留下下面的开放问题:
- Are there pivot rules which lead to polynomial-time Simplex variants?
- Do all polytopal graphs have polynomially-bounded diameter?
整数规划[编辑]
要求所有的未知量都为整数的线性规划问题叫做整数规划(integer programming, IP)或整数线性规划(integer linear programming, ILP)问题。相对于即使在最坏情况下也能有效率地解出的线性规划问题,整数规划问题的最坏情况是不确定的,在某些实际情况中(有约束变量的那些)为NP困难问题。
0-1整数规划是整数规划的特殊情况,所有的变量都要是0或1(而非任意整数)。这类问题亦被分类为NP困难问题。
只要求当中某几个未知数为整数的线性规划问题叫做混合整数规划(mixed integer programming, MIP)问题。这类问题通常亦被分类为NP困难问题。
存在着几类IP和MIP的子问题,它们可以被有效率地解出,最值得注意的一类是具有完全单位模约束矩阵,和约束条件的右边全为整数的一类。
一个解决大型整数线性规划问题的先进算法为delayed column generation。