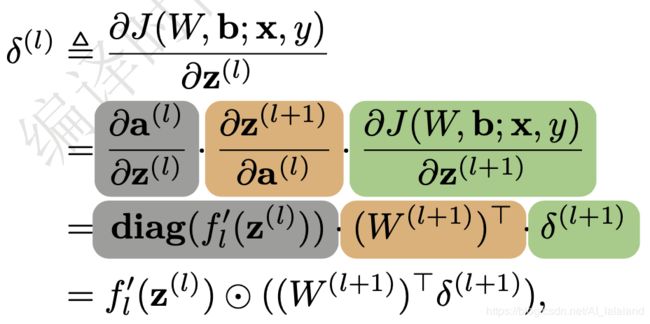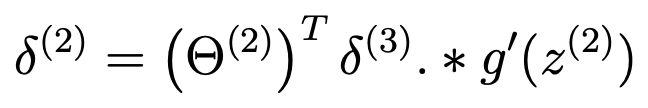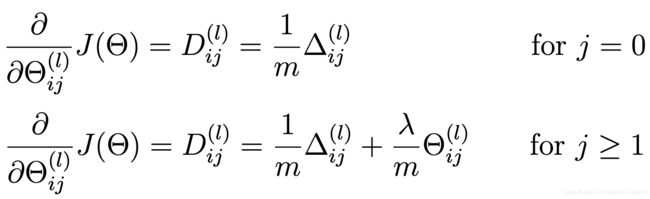吴恩达机器学习CS229A_EX4_神经网络与反向传播算法_Python3

神经网络与反向传播算法

模型是前馈神经网络，优化方法是梯度下降法，求偏导的方式是反向传播算法，数据集依然是手写数字。

本文关于反向传播算法 BP，附了一些数学解释，详细讲解了算法过程。

关于前向传播算法 FP，可以参考：吴恩达机器学习CS229A_EX3_LR与NN手写数字识别_Python3

特别注意：区分矩阵点乘 @ 和矩阵乘法 * ，写错的话可能会导致难以 debug 的错误。

---

导入并初始化数据，这里用了 sklearn 的库函数生成读取的标签集对应 one-hot 的输出形式。

将 theta1 和 theta2 以向量形式初始化（用于后续给执行梯度下降的库函数传参），并且将所有数值随机化到 -0.125 ～ +0.125 之间，如果不做随机，神经网络的权重参数会出现大量相同的冗余情况。

import numpy as np
from scipy.io import loadmat
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder

def loadData(filename):
    return loadmat(filename)

def initData(data, input_size, hidden_size, output_size):
    # X
    X = data['X']
    # y
    y_load = data['y']
    encoder = OneHotEncoder(sparse=False)
    y = encoder.fit_transform(y_load)
    # 随机化 theta1/theta2 in vectors
    params = (np.random.random(size = hidden_size * (input_size + 1) + output_size * (hidden_size + 1)) - 0.5) * 0.25
    return X, y_load, y, params

---

两个辅助函数：

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def sigmoid_gradient(z):
    return sigmoid(z) * (1 - sigmoid(z))

---

神经网络的结构是输入层 400+1，隐藏层 25+1，输出层 10：

前向传播算法（EX3 中已做）：

def FP(X, theta1, theta2):
    m = X.shape[0]
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 @ theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 @ theta2.T
    h = sigmoid(z3)
    return a1, z2, a2, z3, h

根据公式计算 cost：

def cost(X, y, theta1, theta2, lamda):
    m = len(y)
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    J = 0
    for i in range(m):
        first = - y[i,:] * np.log(h[i,:])
        second = - (1 - y[i,:]) * np.log(1 - h[i,:])
        J += np.sum(first + second)
    J = J / m
    # 正则化项
    J += (float(lamda) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
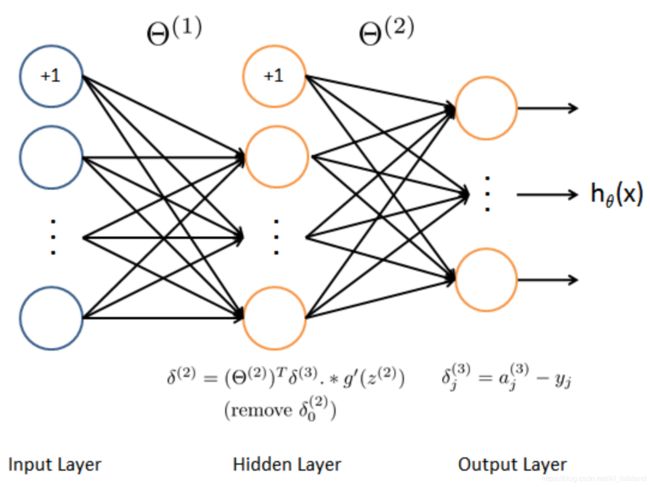
    return J

---

---

整个程序的难点是反向传播算法，先简述一下算法原理（这部分吴恩达老师的课程讲的很简略，最好还是找一些资料补一下）：

首先要明白一点，BP 做的事情是求代价函数 J 对参数 theta (也可以用 weight 表示)的偏导数，根据链式法则，表示如下：

其中第一项定义为误差项，用 δ 表示，其直观的数学含义是第 l 层的神经元的数值 z 的微变化对 NN 输出的误差的影响，或者是说，NN 最终输出的误差，对第 l 层神经元的敏感程度。

对第二项：

很好求得：

 再来看第一项，同样是使用链式求导法则：

 至此，我们就得到了从输出层逐层向前求 J 对 theta(weight) 偏导的方法，可以结合下面的具体算法和程序对照起来看。

---

首先使用前向传播算法，依次计算得到 a1、 z2、 a2、 z3、 h，这里 h 即为 a3。

接着对各个样本 k 依次处理：

    计算输出层的 error：

    计算隐藏层的 error：

    将求得的梯度累加到 delta1、delta2：

将累加值除以样本数 m，并加上正则化项，即得到了最终求得的偏导结果：

def BP(params, input_size, hidden_size, output_size, X, y, lamda):
    # 从 params 向量中提取 theta1、theta2 转化为 np.array 格式
    theta1 = np.array(np.reshape(params[: hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.array(np.reshape(params[hidden_size * (input_size + 1):], (output_size, (hidden_size + 1))))
    # 利用 FP 计算当前参数下得到的各个层的数值
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    # 初始化 delta1、delta2
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)
    # 计算 cost
    J = cost(X, y, theta1, theta2, lamda)
    # 样本数
    m = X.shape[0]
    # BP ：逐个样本处理
    for t in range(m):
        # 抽取该样本的 FP 数值
        a1t = a1[t, :].reshape(1, 401)  # (1, 401)
        z2t = z2[t, :].reshape(1, 25)  # (1, 25)
        a2t = a2[t, :].reshape(1, 26)  # (1, 26)
        ht = h[t, :].reshape(1, 10)  # (1, 10)
        yt = y[t, :].reshape(1, 10)  # (1, 10)
        # 输出层 error
        d3t = ht - yt  # (1, 10)
        # 隐藏层 error
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = (theta2.T @ d3t.T).T * sigmoid_gradient(z2t) # (1, 26)
        # 将 error 累加到 delta
        delta1 = delta1 + (d2t[:, 1:]).T.reshape(25, 1) @ a1t
        delta2 = delta2 + d3t.T.reshape(10, 1) @ a2t
    # 得到最终的偏导数值
    delta1 = delta1 / m
    delta2 = delta2 / m
    # 添加正则化项
    delta1[:, 1:] = delta1[:, 1:] + (theta1[:, 1:] * lamda) / m
    delta2[:, 1:] = delta2[:, 1:] + (theta2[:, 1:] * lamda) / m
    # 将 delta1、delta2 转化为 np.array 格式用于传参
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    return J, grad

将上面描述的具体过程和公式对应程序一步一步看，还是比较容易看明白的，但是要深入理解为什么这么做，最好还是参阅讲述 BP 的数学推导的资料。

---

接下来一步是吴恩达老师强烈建议的梯度检测过程：

使用求近似微分的方式检测 BP 算法是否正确，因为有的时候你写的错误的 BP 算法可以运行，但是得到的结果是错误的。

这个方法比较适用于处理很大的数据集或者训练很复杂的神经网络架构，本例程训练 NN 的时间远小于梯度检测的时间，这里就不做这一步了。

---

最后就是执行和测试算法，因为 NN 的 cost 函数是非凸的，每次结果可能不同，这里贴了一个正确率比较高的：

def predict(fmin_x, input_size, hidden_size, output_size, X, y_load):
    theta1 = np.array(np.reshape(fmin_x[ : hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.array(np.reshape(fmin_x[hidden_size * (input_size + 1) : ], (output_size, (hidden_size + 1))))
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    y_pred = np.array(np.argmax(h, axis=1) + 1)
    correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y_load)]
    accuracy = (sum(map(int, correct)) / float(len(correct)))
    print('accuracy = {0}%'.format(accuracy * 100))

def main():
    input_size = 400
    hidden_size = 25
    output_size = 10
    lamda = 0.1

    data = loadData('ex4data1.mat')
    X, y_load, y, params = initData(data, input_size, hidden_size, output_size)
    #gradient_check(params, input_size, hidden_size, output_size, X, y, lamda)
    fmin = minimize(fun=BP, x0=params, args=(input_size, hidden_size, output_size, X, y, lamda),\
                    method='TNC', jac=True, options={'maxiter': 250})
    print(fmin)
    predict(fmin.x, input_size, hidden_size, output_size, X, y_load)

accuracy = 99.92%

Process finished with exit code 0

---

最后可视化了 theta1，不过貌似依旧看不出什么：

def showHidden(fmin_x, input_size, hidden_size):
    theta1 = np.array(np.reshape(fmin_x[: hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    hidden_layer = theta1[:, 1:]
    fig, ax_array = plt.subplots(nrows=5, ncols=5, sharey=True, sharex=True, figsize=(5, 5))
    for r in range(5):
        for c in range(5):
            ax_array[r, c].matshow(hidden_layer[5 * r + c].reshape((20, 20)), cmap=matplotlib.cm.binary)
            plt.xticks(np.array([]))
            plt.yticks(np.array([]))
    plt.show()

 

---

最后贴出完整程序：

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder

def loadData(filename):
    return loadmat(filename)

def initData(data, input_size, hidden_size, output_size):
    # X
    X = data['X']
    # y
    y_load = data['y']
    encoder = OneHotEncoder(sparse=False)
    y = encoder.fit_transform(y_load)
    # 随机化 theta1/theta2 in vectors
    params = (np.random.random(size = hidden_size * (input_size + 1) + output_size * (hidden_size + 1)) - 0.5) * 0.25
    return X, y_load, y, params

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def FP(X, theta1, theta2):
    m = X.shape[0]
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 @ theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 @ theta2.T
    h = sigmoid(z3)
    return a1, z2, a2, z3, h

# 计算 cost
def cost(X, y, theta1, theta2, lamda):
    m = len(y)
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    J = 0
    for i in range(m):
        first = - y[i,:] * np.log(h[i,:])
        second = - (1 - y[i,:]) * np.log(1 - h[i,:])
        J += np.sum(first + second)
    J = J / m
    # 正则化项
    J += (float(lamda) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
    return J

def sigmoid_gradient(z):
    return sigmoid(z) * (1 - sigmoid(z))

def BP(params, input_size, hidden_size, output_size, X, y, lamda):
    # 从 params 向量中提取 theta1、theta2 转化为 np.array 格式
    theta1 = np.array(np.reshape(params[: hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.array(np.reshape(params[hidden_size * (input_size + 1):], (output_size, (hidden_size + 1))))
    # 利用 FP 计算当前参数下得到的各个层的数值
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    # 初始化 delta1、delta2
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)
    # 计算 cost
    J = cost(X, y, theta1, theta2, lamda)
    # 样本数
    m = X.shape[0]
    # BP ：逐个样本处理
    for t in range(m):
        # 抽取该样本的 FP 数值
        a1t = a1[t, :].reshape(1, 401)  # (1, 401)
        z2t = z2[t, :].reshape(1, 25)  # (1, 25)
        a2t = a2[t, :].reshape(1, 26)  # (1, 26)
        ht = h[t, :].reshape(1, 10)  # (1, 10)
        yt = y[t, :].reshape(1, 10)  # (1, 10)
        # 输出层 error
        d3t = ht - yt  # (1, 10)
        # 隐藏层 error
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = (theta2.T @ d3t.T).T * sigmoid_gradient(z2t) # (1, 26)
        # 将 error 累加到 delta
        delta1 = delta1 + (d2t[:, 1:]).T.reshape(25, 1) @ a1t
        delta2 = delta2 + d3t.T.reshape(10, 1) @ a2t
    # 得到最终的偏导数值
    delta1 = delta1 / m
    delta2 = delta2 / m
    # 添加正则化项
    delta1[:, 1:] = delta1[:, 1:] + (theta1[:, 1:] * lamda) / m
    delta2[:, 1:] = delta2[:, 1:] + (theta2[:, 1:] * lamda) / m
    # 将 delta1、delta2 转化为 np.array 格式用于传参
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    return J, grad

def gradient_check(params, input_size, hidden_size, output_size, X, y, lamda):
    J, grad = BP(params, input_size, hidden_size, output_size, X, y, lamda)
    theta1 = np.array(np.reshape(params[: hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.array(np.reshape(params[hidden_size * (input_size + 1):], (output_size, (hidden_size + 1))))
    costArray = np.zeros((len(params), 2))
    for i in range(0, hidden_size - 1):
        for j in range(0, input_size):
            item = i * hidden_size + j
            theta1[i][j] += 0.001
            costArray[item][0] = cost(X, y, theta1, theta2, lamda)
            theta1[i][j] -= 0.002
            costArray[item][1] = cost(X, y, theta1, theta2, lamda)
            theta1[i][j] += 0.001
    for i in range(0, output_size - 1):
        for j in range(0, hidden_size):
            item = hidden_size * (input_size + 1) + i * output_size + j - 1
            theta1[i][j] += 0.001
            costArray[item][0] = cost(X, y, theta1, theta2, lamda)
            theta1[i][j] -= 0.002
            costArray[item][1] = cost(X, y, theta1, theta2, lamda)
            theta1[i][j] += 0.001
    costArray[:, 0] = (costArray[:, 0] - costArray[:, 1]) / 0.002
    costArray[:, 1] = costArray[:, 0] - grad
    print('max error = {0}%'.format(max(costArray[:, 1])))

def predict(fmin_x, input_size, hidden_size, output_size, X, y_load):
    theta1 = np.array(np.reshape(fmin_x[ : hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.array(np.reshape(fmin_x[hidden_size * (input_size + 1) : ], (output_size, (hidden_size + 1))))
    a1, z2, a2, z3, h = FP(X, theta1, theta2)
    y_pred = np.array(np.argmax(h, axis=1) + 1)
    correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y_load)]
    accuracy = (sum(map(int, correct)) / float(len(correct)))
    print('accuracy = {0}%'.format(accuracy * 100))

def showHidden(fmin_x, input_size, hidden_size):
    theta1 = np.array(np.reshape(fmin_x[: hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    hidden_layer = theta1[:, 1:]
    fig, ax_array = plt.subplots(nrows=5, ncols=5, sharey=True, sharex=True, figsize=(5, 5))
    for r in range(5):
        for c in range(5):
            ax_array[r, c].matshow(hidden_layer[5 * r + c].reshape((20, 20)), cmap=matplotlib.cm.binary)
            plt.xticks(np.array([]))
            plt.yticks(np.array([]))
    plt.show()

def main():
    input_size = 400
    hidden_size = 25
    output_size = 10
    lamda = 1

    data = loadData('ex4data1.mat')
    X, y_load, y, params = initData(data, input_size, hidden_size, output_size)
    #gradient_check(params, input_size, hidden_size, output_size, X, y, lamda)
    fmin = minimize(fun=BP, x0=params, args=(input_size, hidden_size, output_size, X, y, lamda),\
                    method='TNC', jac=True, options={'maxiter': 250})
    print(fmin)
    predict(fmin.x, input_size, hidden_size, output_size, X, y_load)
    showHidden(fmin.x, input_size, hidden_size)

main()