用最小二乘法和梯度下降法求解回归问题(Matlab实现)
用最小二乘法和梯度下降法求解回归问题(Matlab实现)
文章目录
- 用最小二乘法和梯度下降法求解回归问题(Matlab实现)
- 1. 实验任务
- 2. 实现原理
- 2.1 最小二乘法实现原理
- 2.2 梯度下降法实现原理
- 3. 程序结构及具体实现
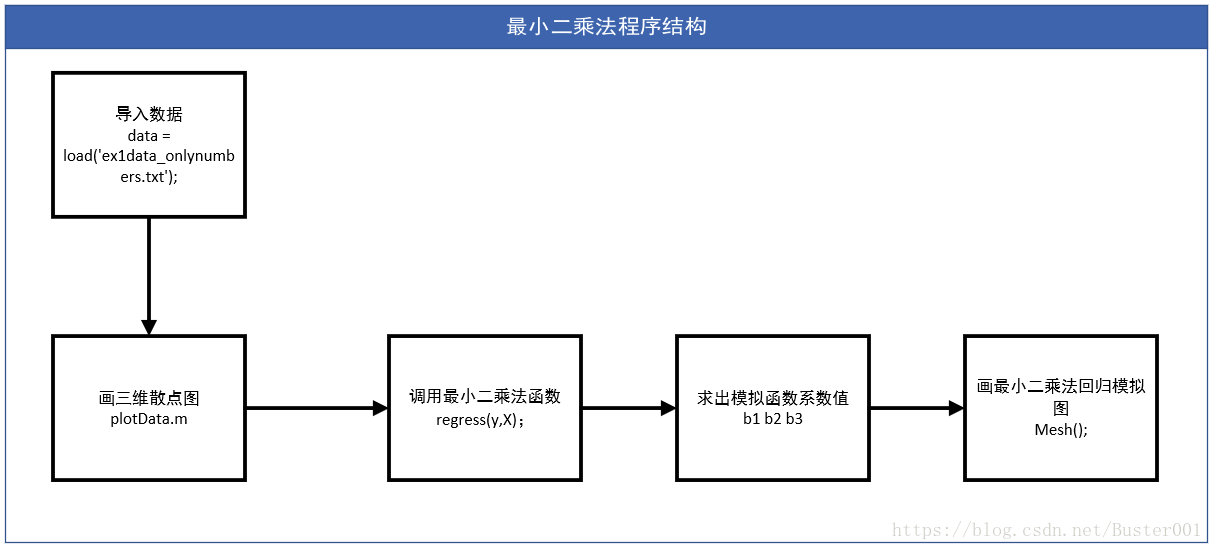
- 3.1 最小二乘法程序结构及实现
- (1)执行文件main_LeastSquare.m
- (2)函数文件plotData.m
- (3)函数文件LeastSqaure.m
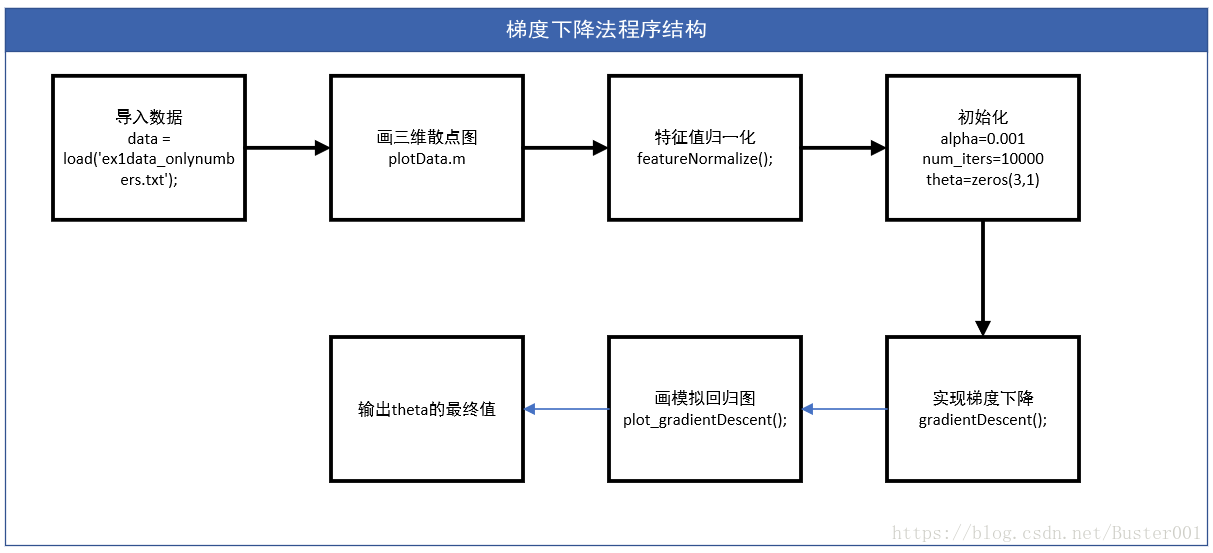
- 3.2 梯度下降法程序结构及实现
- (1)执行文件main_gradientDescent.m
- (2)函数文件plotData.m
- (3)函数文件featureNormalize.m
- (4)函数文件computeCost.m
- (5)函数文件gradientDescent.m
- (6)函数文件plot_gradientDescent.m
- 4. 说明
1. 实验任务
现有一家连锁饭店年利润和该饭店所在的城市人口与城市面积的数据(具体参见ex1data_onlynumbers.txt),请用回归方法找出饭店的利润和城市人口与城市面积之间的关系。
1)用最小二乘法求解回归问题。(要能显示散点图、回归结果图)
2)用梯度下降法求解回归问题(要能显示散点图、迭代过程、回归结果图)。
说明数据文件是n*3的数据。
本博客所有的资料和代码都在这里:https://pan.baidu.com/s/1dBTCC2KB2eTw9yMcRhLsqA
2. 实现原理
2.1 最小二乘法实现原理
假设城市人口为X1,城市面积为X2,饭店利润为y。
通过函数h = b1 + b2X1 + b3X2 来模拟y和X1、X2之间的关系,同时使函数值h与y误差的平方和最小。
即 s u m i = 0 m ( h − y ) 2 \ sum_{i=0}^m (h-y)^2 sumi=0m(h−y)2 的值最小,进而求得模拟函数的系数b1、b2、b3。m为样本的数量。
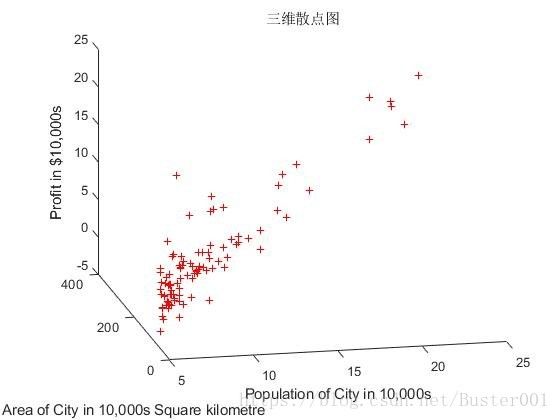
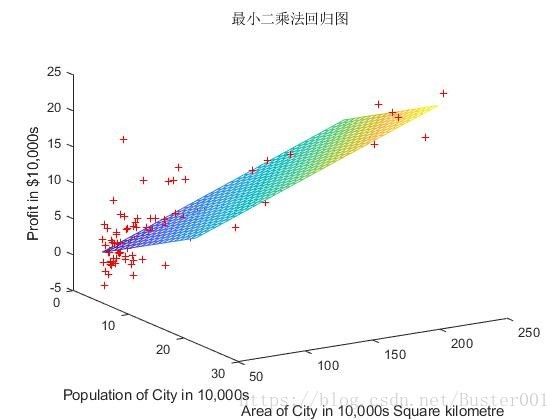
图2-1为根据原始数据画出的三维散点图。通过Matlab最小二乘法处理数据后,得到系数值b1、b2、b3。
最小二乘法的回归函数为:h = b1 + b2X1 + b3X2。即可求得。
2.2 梯度下降法实现原理
假设城市人口为X1,城市面积为X2,饭店利润为y。
通过函数h = theta1 + theta2X1 + theta3X2来模拟y和X1、X2之间的关系,通过迭代更新的方式来求取theta1、theta2、theta3的值。
Cost function: J = 1 2 m s u m i = 0 m ( h − y ) 2 \ J= \frac{1}{2m} sum_{i=0}^m (h-y)^2 J=2m1sumi=0m(h−y)2
更新theta值:
t h e t a 1 = t h e t a 1 − a l p h a 1 m s u m i = 0 m ( ( h − y ) ∗ 1 ) \ theta1 = theta1 - alpha \frac{1}{m} sum_{i=0}^m ((h-y)*1) theta1=theta1−alpham1sumi=0m((h−y)∗1)
t h e t a 2 = t h e t a 2 − a l p h a 1 m s u m i = 0 m ( ( h − y ) ∗ X 1 ) \ theta2 = theta2 - alpha \frac{1}{m} sum_{i=0}^m ((h-y)*X1) theta2=theta2−alpham1sumi=0m((h−y)∗X1)
t h e t a 3 = t h e t a 3 − a l p h a 1 m s u m i = 0 m ( ( h − y ) ∗ X 2 ) \ theta3 = theta3 - alpha \frac{1}{m} sum_{i=0}^m ((h-y)*X2) theta3=theta3−alpham1sumi=0m((h−y)∗X2)
上面的表达式中:alpha表示学习率,m表示样本数量,theta分别表示各项系数。
梯度下降法通过迭代的方式,一次一次的更新theta的值,来达到减小Cost function值的目的。最终可以得到theta1、theta2、theta3的值。
3. 程序结构及具体实现
3.1 最小二乘法程序结构及实现
(1)执行文件main_LeastSquare.m
最小二乘法执行文件是main_LeastSquare.m, 具体代码如下所示:
%% 执行本文件可以得到最小二乘法的过程和结果
%% Initialization
clear ; close all; clc
%% ======================= Part 1: 画二维和三维散点图 =======================
fprintf('Plotting Data ...\n')
data = load('ex1data_onlynumbers.txt'); % 导入文件
X_origin = data(:, 1:end-1); y = data(:, end); % 通过导入的文件,对矩阵赋值
m = length(y); % number of training examples
% Plot Data
plotData(X_origin, y); % 调用plotData()函数画散点图:二维和三维散点图
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ======================= Part 2: 最小二乘法 =======================
LeastSqaure(X_origin, y); % 调用LeastSqaure()函数,实现最小二乘法
(2)函数文件plotData.m
下面是plotData()函数的实现代码,保存文件为plotData.m,主要实现画出原始数据的二维和三维散点图。
function plotData(x, y)
% 本函数画出原始数据的二维和三维散点图
figure; % open a new figure window
plot(x(:,1), y, 'r+', 'MarkerSize', 5);
xlabel('Population of City in 10,000s');
ylabel('Profit in $10,000s');
figure;
plot(x(:,2), y, 'r+', 'MarkerSize', 5);
xlabel('Area of City in Square kilometre');
ylabel('Profit in $10,000s');
figure;
plot3(x(:,1),x(:,2),y,'r+', 'MarkerSize', 5);
xlabel('Population of City in 10,000s');
ylabel('Area of City in 10,000s Square kilometre');
zlabel('Profit in $10,000s');
title('三维散点图');
end
(3)函数文件LeastSqaure.m
下面是LeastSqaure()函数实现代码,保存文件为LeastSqaure.m,主要实现最小二乘法进行数据拟合,求出系数b,并画出回归拟合图形。
function LeastSqaure(x,y)
% 本函数对最小二乘法进行数据拟合
% 通过回归方程拟合求出系数b
% 最后画出回归拟合图形
%=============================================================
x1 = x(:, 1); %x1表示X_origin的第一列,即城市人口
x2 = x(:, 2); %x2表示X_origin的第二列,即城市面积
X = [ones(size(x1)), x1, x2]; % 需要在原有的变量矩阵前面加一列1, 这是为了方便计算回归系数b(1)
b = regress(y,X) %b为回归系数
plot3(x1,x2,y,'r+', 'MarkerSize', 5) % x1, x2, y的三维散点图
hold on %接着在上面的图中画图
x1fit = min(x1):1:max(x1); % 定义x1的采样区间与间隔
x2fit = min(x2):5:max(x2); % 定义x2的采样区间与间隔
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit); % 生成网格采样点
YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT; % 回归拟合方程
mesh(X1FIT,X2FIT,YFIT) % 回归拟合之后的结果图形
% surf(X1FIT, X2FIT, YFIT)
%下面是x, y, z轴的坐标含义
xlabel('Population of City in 10,000s');
ylabel('Area of City in 10,000s Square kilometre');
zlabel('Profit in $10,000s');
title('最小二乘法回归图');
view(50,10) % 视点函数,看图的视角
%===============参数b的输出结果============
% b =
% -3.950289763365570
% 0.446853466426605
% 0.071743334500185
end
由上面的三个文件即可完成最小二乘法求解回归问题。main_LeastSquare.m为执行文件,plotData.m为函数文件,主要实现画出原始数据的二维和三维散点图;LeastSqaure.m为函数文件,主要实现最小二乘法进行数据拟合,求出系数b,并画出回归拟合图形。
3.2 梯度下降法程序结构及实现
(1)执行文件main_gradientDescent.m
梯度下降法执行文件为main_gradientDescent.m,实现代码如下:
%% 执行本文件可以得到梯度下降法的过程和结果
%% Initialization
clear ; close all; clc
%% ======================= Part 1: 画二维和三维散点图 =======================
fprintf('Plotting Data ...\n')
data = load('ex1data_onlynumbers.txt'); % 导入文件
X_origin = data(:, 1:end-1); y = data(:, end); % 通过导入的文件,对矩阵赋值
m = length(y); % number of training examples
% Plot Data
plotData(X_origin, y); % 画散点图:二维和三维散点图
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 2: 梯度下降法 ===================
% 调用特征归一化函数
[X_norm, mu, sigma] = featureNormalize(X_origin);
fprintf('Running gradient descent ...\n');
% 初始化
alpha = 0.001; % 学习率
num_iters = 10000; % 迭代次数
theta = zeros(3, 1); % 自变量的系数
J0 = computeCost(X_norm,y,theta) % J的初始计算值
%========调用gradientDescent()函数==========================
[theta, J_history] = gradientDescent(X_norm, y, theta, alpha, num_iters);
%======================画图==================
plot_gradientDescent(X_norm,y,J_history,theta)
fprintf('======================================================\n');
fprintf('theta的最终值为:\n');
fprintf(' %f \n', theta);
fprintf('\n');
(2)函数文件plotData.m
这里plotData()函数与上面最小二乘法相同,函数文件也是plotData.m,所以就不在这里赘述。
(3)函数文件featureNormalize.m
接着就是调用特征归一化函数featureNormalize(),保存为featureNormalize.m文件。代码实现如下:
function [X_norm, mu, sigma] = featureNormalize(X)
% 特征值归一化函数
X_norm = zeros(size(X)); % 将X的所有元素都设为0,并复制给X_norm
mu = zeros(1, size(X, 2)); % 生成一个1*size(X, 2)的矩阵给mu
sigma = zeros(1, size(X, 2)); % 生成一个1*size(X, 2)的矩阵给sigma
m = size(X, 1); % m为每个特征的样本数
% ====================== YOUR CODE HERE ======================
mu = mean(X); % 求出每个自变量的平均值
sigma = max(X) - min(X); % 每个自变量的最大值-最小值
X_norm = (X - (ones(m,1)*mu)).* ((ones(m,1)*sigma).^(-1)); % (X-均值)/(最大值-最小值)
X_norm = [ones(size(X_norm(:, 1))), X_norm(:, 1), X_norm(:, 2)]; % 需要在原有的变量矩阵前面加一列1, 这是为了方便计算梯度下降
% ============================================================
end
(4)函数文件computeCost.m
然后对一些参数进行初始化之后,调用了computeCost()函数计算J的值,保存文件为computeCost.m,实现代码如下:
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% Cost函数定义如下:
% J = ((X*theta-y)')*(X*theta-y)/(2*m);
% sum = 0;
% for i = 1:m
% sum = sum + (X(i,:)*theta - y(i))^2;
% end
% J = sum/(2*m);
J = sum((X*theta - y).^2)/(2*m); %Cost函数实现
end
(5)函数文件gradientDescent.m
接着就是调用gradientDescent()函数实现梯度下降,保存文件为gradientDescent.m,实现代码如下:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%梯度下降函数,实现梯度下降过程,并输出每一次迭代的theta值。
m = length(y); % 训练样本数量
J_history = zeros(num_iters, 1); % 记录每一次迭代J的取值
n = size(X,2); % 自变量的数量
temp = zeros(n,1); % 自变量的偏导数
% 迭代
for iter = 1:num_iters
% 自变量求偏导数循环
for j = 1:n
temp(j) = sum((X*theta - y)'*X(:,j)); % 变量的偏导数项
end
theta = theta - temp* alpha/m; % theta更新
J_history(iter) = computeCost(X, y, theta); % 记录每一次迭代J的取值
% 输出每一次迭代,theta的值
fprintf('num_iters = %d\n', iter);
fprintf('%.6f\t %.6f\t %.6f', theta(1), theta(2), theta(3));
fprintf('\n');
end
end
(6)函数文件plot_gradientDescent.m
实现梯度下降法之后,可以把梯度下降法的模拟图画出来,画图的时候调用plot_gradientDescent()函数,保存文件为plot_gradientDescent.m,实现代码如下:
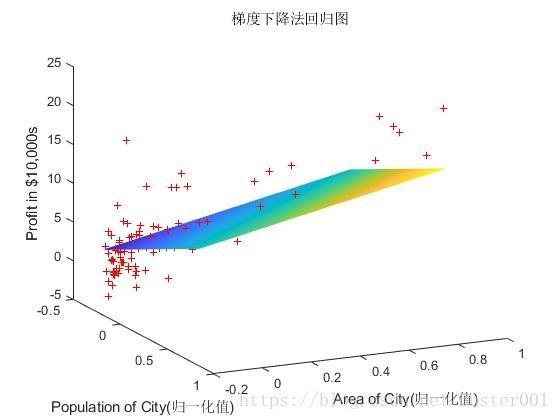
function plot_gradientDescent(X,y,J_history,theta)
% 梯度下降法之后的回归图形
% 回归图形是归一化后的数据做成的图形
plot3(X(:, 2),X(:, 3),y,'r+', 'MarkerSize', 5) % x1, x2, y的三维散点图
hold on %接着在上面的图中画图
x1fit = min(X(:, 2)):0.01:max(X(:, 2)); % 定义x1的采样区间与间隔
x2fit = min(X(:, 3)):0.01:max(X(:, 3)); % 定义x2的采样区间与间隔
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit); % 生成网格采样点
YFIT = theta(1) + theta(2)*X1FIT + theta(3)*X2FIT; % 梯度下降法回归拟合方程
mesh(X1FIT,X2FIT,YFIT) % 回归拟合之后的结果图形
% surf(X1FIT, X2FIT, YFIT)
%下面是x, y, z轴的坐标含义
xlabel('Population of City(归一化值)');
ylabel('Area of City(归一化值)');
zlabel('Profit in $10,000s');
title('梯度下降法回归图');
view(50,10) % 视点函数,看图的视角
% 迭代次数与cost函数J之间的关系图
figure;
plot(1:numel(J_history), J_history, '-', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
title('Costfunction与迭代次数的之间关系');
end
上面的6个文件,即可完成梯度下降法求解回归问题。最后可以得到theta1、theta2、theta3的值,并且画出J与迭代次数的图像和梯度下降法的拟合图像。
4. 说明
- 运行环境为Matlab2017b,系统为Win10。
- Matlab的文件必须要在同一个文件夹里,才能够运行。