OpenGL LookAt、Camera摄像机
摄像机/观察空间
程序执行效果
摄像机代码
// 摄像机
view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
ourShader.setMat4("view", view);
实际上就是得到一个View Matrix,这样就可以传送给shader program用于计算从本地坐标系向投影坐标系、剪裁坐标系进行转换。
glm::lookAt(eye, center, up)
eye实际上就是摄像机的位置
center就是摄像机的方向
up就是上轴
eye -> cameraPos
center -> cameraPos + cameraFront
up -> cameraUp
摄像机的位置很好理解,就是3D空间中的一个点P(Vector3{x, y, z})
那么方向的量就是A(Vector3{x, y, z})到B(Vector3{x, y, z})指向(tail, head指向) [下面的代码叫方向向量不恰当,因为是相反的]
我们将两个点的空间坐标通过向量的标准化求得方向(空间的点不是向量,和长度一样是标量):
1、cameraPos:
vec3(0.0, 0.0, 3.0);
2、cameraFront:
vec3(0.0, 0.0, -1.0); // z 轴相反的方向为摄像机向前
3、cameraPos - cameraFront:
v1 = vec3(x: 0.0, y: 0.0, z: 3.0) , v2 = vec3(x: 0.0, y: 0.0, z: -1.0)
(v1) + (-v2) = (0.0, 0.0, 3.0 + -0.0, -0.0, 1.0)
(0.0, 0.0, 4.0)
如果是相加的话:
cameraPos - cameraFront = (0.0, 0.0, 2.0)
4、cameraDirection = glm::normalize(cameraPos + cameraFront) // 也可以不用这样,直接将cameraPos + cameraFront作为方向
模等于0的向量成为0向量,模等于1的向量叫做单位向量。注意零向量的方向是任意的。由一个向量v求与它同方向的单位向量过程称为标准化(normalization),这个单位向量成为标准化向量(normalized vector)。
公式:
vector normalize = v|v| (v≠0)
carmeraDirection = (0.0, 0.0, 1.0)
5、cameraUp
右轴:
我们需要的另一个向量是一个右向量(Right Vector),它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧:先定义一个上向量(Up Vector)。接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量,因此我们会得到指向x轴正方向的那个向量(如果我们交换两个向量叉乘的顺序就会得到相反的指向x轴负方向的向量):
glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
现在我们已经有了x轴向量和z轴向量,获取一个指向摄像机的正y轴向量就相对简单了:我们把右向量和方向向量进行叉乘:
glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
cameraUp = cross(cameraDirection, cross(up, cameraDirection))
glm::cross是求向量的叉积(向量乘法的叉乘)的:
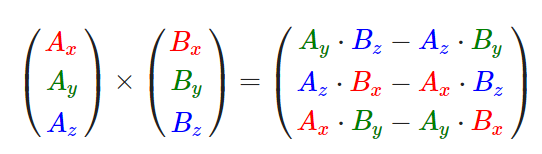
cameraUp = (0, 1, 0) // Y axis its Up axis
glm::vec3 Pos = glm::vec3(0.0f, 0.0f, 3.0f);
glm::vec3 Target = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 Direction = glm::normalize(Pos - Target);
glm::vec3 Up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 Right = glm::normalize(glm::cross(Up, Direction));
glm::vec3 CamUp = glm::cross(Direction, Right);
6、得到了摄像机的向量后,我们通过LookAt Matrix来求得View Matrix:
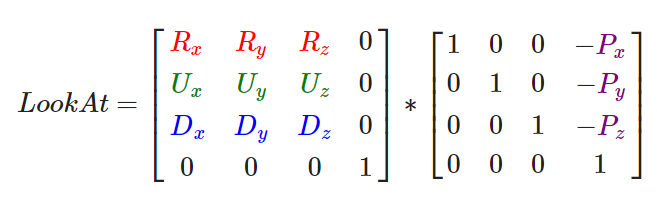
R -> Right Vector右向量
U -> Up 是上向量(Up axis)
D -> Direction 方向向量
P -> Camera Position 摄像机的位置(空间中的点坐标)
求出的矩阵就是我们需要的View Coordinate(Space)需要的View Matrix
摄像机的移动
FPS游戏中我们通常用W,S,A,D,来控制前进、后退、左移、右移。
实际上是对摄像机的位置进行操作,上面提到的cameraPos。
移动设计到一个变量,就是速度(我们暂时没有使用物理公式求速度,这里属于均速位移)
front(position) = front(position) + speed * position
back(position) = back(position) - speed * position
left(position) = left(position) - normalize(cross(front, up)) * speed;
right(position) = right(position) + normalize(cross(front, up)) * speed;
代码如下:
GLfloat cameraSpeed = 2.5 * deltaTime;
if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
cameraPos += cameraSpeed * cameraFront;
if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
cameraPos -= cameraSpeed * cameraFront;
if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
欧拉角与摄像机鼠标控制视野转动
欧拉角
欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值,由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角:俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll),下面的图片展示了它们的含义:
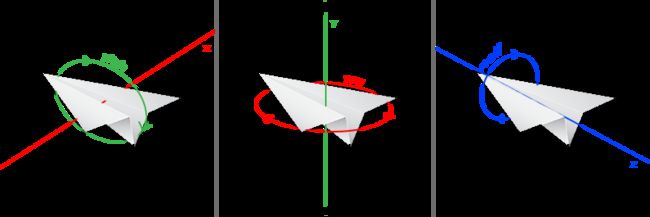
关于俯仰、滚转、偏航,玩过模拟飞行的,例如DCS或则Falcon,Simulated flight X的肯定会了解这个,而上图也是用了一个纸飞机来展示,在模拟飞行中,实际上也是这样控制的,无非就是多了物理学应用,对空气动力学进行一定模拟实现。
而这里我们解决的是使用俯仰与偏航完成摄像机的视角控制(现在新的一些FPS游戏中也可以控制滚转来控制偏头射击(Q、E控制))。
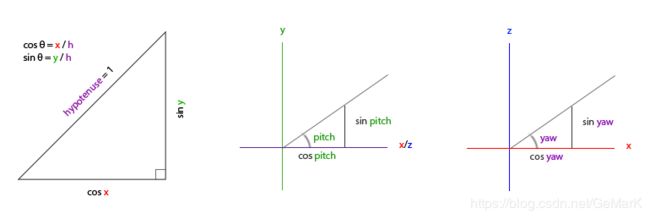
如果我们把斜边边长定义为1,我们就能知道邻边的长度是cos x/h=cos x/1=cos x,它的对边是sin y/h=sin y/1=sin y。这样我们获得了能够得到x和y方向长度的通用公式,它们取决于所给的角度。我们使用它来计算方向向量的分量:
弧度转角度:角度 = 弧度 * (180.0 / PI)
角度转弧度:弧度 = 角度 * (PI / 180.0)
PI派约等于:3.14159265359
sin(pitch * PI / 180.0)
我们可以初始化pitch为0.0
转半圈会旋转360/2 = 180度,向右旋转1/5圈表示向右旋转360/5 = 72度。
代码如下:
direction.y = sin(glm::radians(pitch));
这里我们只更新了y值,仔细观察x和z分量也被影响了。从三角形中我们可以看到它们的值等于:
direction.x = cos(glm::radians(pitch));
direction.z = cos(glm::radians(pitch));
就像俯仰角的三角形一样,我们可以看到x分量取决于cos(yaw)的值,z值同样取决于偏航角的正弦值。把这个加到前面的值中,会得到基于俯仰角和偏航角的方向向量:
// 译注:direction代表摄像机的前轴(Front),这个前轴是上面图中第一个展示
direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); 第二个摄像机的方向向量是相反的
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));