MVP变换矩阵推导及C++实现
在进行图像处理时,经常会用到矩阵,尤其在游戏中,基本都会存在一个Camera的概念,实际上,这个Camera一般就是矩阵或者是对矩阵的封装。一个4x4矩阵,可以将平移、旋转、缩放等变换操作包含在内。但是为了便于理解与控制,这个最终的矩阵,往往是由一系列便于理解的参数来运算得出的。而Model-View-Projection变换模型就是最常用,一般来说,我们并不必去实现它们,因为有太多的工具类可以直接使用。但是理解它们的原理会让我们更好的理解3D(包括2D)的图形变换。
矩阵的基础知识
在高数中,我们都学过矩阵的基本运算及一些基本定律。在我之前的博客Android OpenGLES2.0(十)——OpenGL中的平移、旋转、缩放中,也提到了矩阵运算,不过之前的矩阵是使用了Android自带的工具类。在本篇博客中,将会说明如何去实现一个矩阵工具类。所以我们需要对矩阵运算及相关定律理解的更加透彻。
我们所需要使用到的矩阵运算,主要就是矩阵的乘法、转置等相关运算及操作。
向量和矩阵的乘法
我们使用矩阵去实现图形的3D变换,实际上,通常就是对图形的所有点去做3D变换,而每个点的位置,都可以看做是一个向量,同时,向量也是特殊的矩阵。矩阵和列向量的乘法在之前的博客有提到,这里再贴一次。
(1) [ x 1 y 1 z 1 w 1 ] = [ m 1 m 5 m 9 m 13 m 2 m 6 m 10 m 14 m 3 m 7 m 11 m 15 m 4 m 8 m 12 m 16 ] [ x y z 1 ] = [ m 1 ∗ x + m 5 ∗ y + m 9 ∗ z + m 13 m 2 ∗ x + m 6 ∗ y + m 10 ∗ z + m 14 m 3 ∗ x + m 7 ∗ y + m 11 ∗ z + m 15 m 4 ∗ x + m 8 ∗ y + m 12 ∗ z + m 16 ] \left . \begin{bmatrix} x1 \\ y1 \\ z1 \\ w1 \end{bmatrix} = \begin{bmatrix} m1 & m5 & m9 &m13 \\ m2& m6 & m10 &m14\\ m3 & m7 &m11&m15\\ m4&m8&m12&m16 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} m1*x + m5*y + m9*z +m13 \\ m2*x + m6*y + m10*z +m14\\ m3*x + m7*y + m11*z +m15\\ m4*x + m8*y + m12*z +m16 \end{bmatrix} \right .\tag{1} ⎣⎢⎢⎡x1y1z1w1⎦⎥⎥⎤=⎣⎢⎢⎡m1m2m3m4m5m6m7m8m9m10m11m12m13m14m15m16⎦⎥⎥⎤⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡m1∗x+m5∗y+m9∗z+m13m2∗x+m6∗y+m10∗z+m14m3∗x+m7∗y+m11∗z+m15m4∗x+m8∗y+m12∗z+m16⎦⎥⎥⎤(1)
矩阵和行向量的乘法与此类似,只是列向量是右乘,行向量是左乘。
(1) [ x 1 y 1 z 1 w 1 ] = [ x y z 1 ] [ m 1 m 5 m 9 m 13 m 2 m 6 m 10 m 14 m 3 m 7 m 11 m 15 m 4 m 8 m 12 m 16 ] = [ m 1 ∗ x + m 2 ∗ y + m 3 ∗ z + m 4 m 5 ∗ x + m 6 ∗ y + m 7 ∗ z + m 8 m 9 ∗ x + m 10 ∗ y + m 11 ∗ z + m 12 m 13 ∗ x + m 14 ∗ y + m 15 ∗ z + m 16 ] \left . \begin{bmatrix} x1&y1&z1&w1 \end{bmatrix} = \begin{bmatrix} x & y & z & 1 \end{bmatrix} \begin{bmatrix} m1 & m5 & m9 &m13 \\ m2& m6 & m10 &m14\\ m3 & m7 &m11&m15\\ m4&m8&m12&m16 \end{bmatrix} = \begin{bmatrix} m1*x + m2*y + m3*z +m4 \\ m5*x + m6*y + m7*z +m8\\ m9*x + m10*y + m11*z +m12\\ m13*x + m14*y + m15*z +m16 \end{bmatrix} \right .\tag{1} [x1y1z1w1]=[xyz1]⎣⎢⎢⎡m1m2m3m4m5m6m7m8m9m10m11m12m13m14m15m16⎦⎥⎥⎤=⎣⎢⎢⎡m1∗x+m2∗y+m3∗z+m4m5∗x+m6∗y+m7∗z+m8m9∗x+m10∗y+m11∗z+m12m13∗x+m14∗y+m15∗z+m16⎦⎥⎥⎤(1)
矩阵乘法结合律
首先,很明显,根据矩阵乘法的定义,第一个矩阵的列数和第二个矩阵的行数相等,矩阵相乘才有意义。矩阵的运算是不满足交换律的,因为可以相乘的两个矩阵,它们交换顺序后,就不一定能够相乘了。但是,矩阵是满足结合律的,及ABC = A(BC)。这个公式很容易推导,不必细说。
左乘右乘及转置
在OpenGL中,编写shader的时候,我们可以发现矩阵和向量的乘法是矩阵在前,而向量在后的,乘法需要从右向左乘,也就是左乘法,这也说明了OpenGL中使用的是列向量。按照MVP变换的顺序,先Model再View最后Projection,我们在Shader中写法通常为:
gl_Position = projectionMatrix * viewMatrix * modelMatrix * vertexVec;
乍一看,好像和MVP的顺序相反。可以用结合律的方式来理解它,只有这样写,vertexVec才是先经过modelMatrix变换再经过viewMatrix变换,最后经过projectionMatrix变换。
在C++中实现时,我们可以使用中这种方式来实现,也可以按照vertexVec * modelMatrix * viewMatrix * projectionMatrix的方式来实现,但是这个vertexVec是一个行向量,3个Matrix与之前并不相同。这里就又涉及到一个矩阵的操作了——矩阵的转置。矩阵的转置就是把原矩阵的每一行变成一列,列向量变成行向量就是一个矩阵的转置操作。针对上面两种理解方式,有以下公式:
( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
即,矩阵A乘矩阵B,然后转置,其结果与B的转置矩阵乘A的转置矩阵结果相同。在OpenGL中,加载矩阵时,可以设置矩阵是否转置。
MVP矩阵
我们在三维图形中,变换矩阵通常使用的是4*4的矩阵,以表示出三维的旋转与平移,坐标点也会补上w分量,把三维的笛卡尔坐标变为三维齐次坐标,齐次坐标在仿射变换中会发挥重要的作用,而平移旋转操作正好就是仿射变换:
y ⃗ = A x ⃗ + c ⃗ \vec{y} = A\vec{x} + \vec{c} y=Ax+c
其等价于:
[ y ⃗ 1 ] = [ A c ⃗ 0...0 1 ] [ x ⃗ 1 ] \begin{bmatrix} \vec{y} \\ 1 \end{bmatrix}= \begin{bmatrix} A & \vec{c} \\ 0...0 & 1 \end{bmatrix} \begin{bmatrix} \vec{x} \\ 1 \end{bmatrix} [y1]=[A0...0c1][x1]
Model-View-Projection矩阵,Model矩阵表示的是模型的变换矩阵,这个变换是在模型世界中,对模型进行变换的。View矩阵表示的是视界变换矩阵,是将模型从模型世界坐标系变换到相机世界坐标系中。Projection表示的是投影变换矩阵,用于将转换到相机世界左边系中的模型,投影为设备规范化坐标,是为了渲染到屏幕上做准备,其z坐标取值变为了[-1,1]区间的值,而x、y也会被限定到相应的范围之内,具体在投影矩阵中会详细说明。最后,其实还有一步变换,以渲染到2d的屏幕上,这步由渲染器完成,我们并不需要处理,不过在博客后面也会作出说明。
在游戏以及3D图像中,一般会有相机的概念。而相机的参数主要分为两部分,一部分是相机内参,比如相机的焦距、广角等等。另一部分是相机外参,比如相机的位置、朝向等等。实际上,在MVP中,V就是由相机的外参构成,P就是由相机的内参构成。而这些参数相对矩阵数据,更容易让人理解和操作,这也是将一个矩阵,拆分成MVP三个矩阵的好处。
矩阵乘法实现
矩阵数据可以用一个大小为16的float数组来存储。索引值定义如下,M后面跟着两位数字,第一位表示这个数字在矩阵的列数,第二位表示这个数字所在的行数。
static const int M00 = 0;
static const int M10 = 1;
static const int M20 = 2;
static const int M30 = 3;
static const int M01 = 4;
static const int M11 = 5;
static const int M21 = 6;
static const int M31 = 7;
static const int M02 = 8;
static const int M12 = 9;
static const int M22 = 10;
static const int M32 = 11;
static const int M03 = 12;
static const int M13 = 13;
static const int M23 = 14;
static const int M33 = 15;
重载乘法运算符,就是把矩阵乘法用代码来实现以下:
Matrix Matrix::operator*(Matrix &mat) {
Matrix temp;
temp[M00] = value[M00]*mat[M00] + value[M10]*mat[M01] + value[M20]*mat[M02] + value[M30]*mat[M03];
temp[M01] = value[M01]*mat[M00] + value[M11]*mat[M01] + value[M21]*mat[M02] + value[M31]*mat[M03];
temp[M02] = value[M02]*mat[M00] + value[M12]*mat[M01] + value[M22]*mat[M02] + value[M32]*mat[M03];
temp[M03] = value[M03]*mat[M00] + value[M13]*mat[M01] + value[M23]*mat[M02] + value[M33]*mat[M03];
temp[M10] = value[M00]*mat[M10] + value[M10]*mat[M11] + value[M20]*mat[M12] + value[M30]*mat[M13];
temp[M11] = value[M01]*mat[M10] + value[M11]*mat[M11] + value[M21]*mat[M12] + value[M31]*mat[M13];
temp[M12] = value[M02]*mat[M10] + value[M12]*mat[M11] + value[M22]*mat[M12] + value[M32]*mat[M13];
temp[M13] = value[M03]*mat[M10] + value[M13]*mat[M11] + value[M23]*mat[M12] + value[M33]*mat[M13];
temp[M20] = value[M00]*mat[M20] + value[M10]*mat[M21] + value[M20]*mat[M22] + value[M30]*mat[M23];
temp[M21] = value[M01]*mat[M20] + value[M11]*mat[M21] + value[M21]*mat[M22] + value[M31]*mat[M23];
temp[M22] = value[M02]*mat[M20] + value[M12]*mat[M21] + value[M22]*mat[M22] + value[M32]*mat[M23];
temp[M23] = value[M03]*mat[M20] + value[M13]*mat[M21] + value[M23]*mat[M22] + value[M33]*mat[M23];
temp[M30] = value[M00]*mat[M30] + value[M10]*mat[M31] + value[M20]*mat[M32] + value[M30]*mat[M33];
temp[M31] = value[M01]*mat[M30] + value[M11]*mat[M31] + value[M21]*mat[M32] + value[M31]*mat[M33];
temp[M32] = value[M02]*mat[M30] + value[M12]*mat[M31] + value[M22]*mat[M32] + value[M32]*mat[M33];
temp[M33] = value[M03]*mat[M30] + value[M13]*mat[M31] + value[M23]*mat[M32] + value[M33]*mat[M33];
return temp;
}
Model矩阵
Model矩阵用于模型在模型空间的转换(模型空间一般是一个笛卡尔右手坐标系),比如在maya中制作一个模型,Model矩阵,就是相当于在Maya的坐标系下,对模型进行变换。它主要包含旋转、缩放、平移等变换。即,Model矩阵中隐含了三个矩阵——缩放矩阵、平移矩阵、旋转矩阵。根据矩阵不满足交换律的定律,这三个矩阵按照不同的顺序相乘,得到的Model矩阵是不同的。矩阵先平移再缩放和先缩放再平移,得到的结果是明显不同的。它们的顺序一般由变换的需求决定。
平移和缩放的矩阵都再简单不过,直接使用矩阵的乘法,带值进入计算,即可得到缩放矩阵和平移矩阵,唯一比较麻烦的就是旋转矩阵了。旋转矩阵包含三个方向的旋转,依次绕X轴旋转、绕Y轴旋转、绕Z轴旋转。
(绕X轴变换矩阵) [ 1 0 0 0 0 c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 ] \begin{bmatrix} 1 & 0& 0&0 \\ 0& cos \alpha & -sin \alpha &0 \\ 0 & sin \alpha & cos \alpha &0\\ 0 &0&0&1 \end{bmatrix} \tag{绕X轴变换矩阵} ⎣⎢⎢⎡10000cosαsinα00−sinαcosα00001⎦⎥⎥⎤(绕X轴变换矩阵)
(绕Y轴变换矩阵) [ c o s β 0 s i n β 0 0 1 0 0 − s i n β 0 c o s β 0 0 0 0 1 ] \begin{bmatrix} cos \beta &0& sin \beta &0 \\ 0&1&0&0 \\ -sin \beta &0 & cos \beta &0\\ 0 &0&0&1 \end{bmatrix} \tag{绕Y轴变换矩阵} ⎣⎢⎢⎡cosβ0−sinβ00100sinβ0cosβ00001⎦⎥⎥⎤(绕Y轴变换矩阵)
(绕Z轴变换矩阵) [ c o s γ − s i n γ 0 0 s i n γ c o s γ 0 0 0 0 1 0 0 0 0 1 ] \begin{bmatrix} cos \gamma & -sin \gamma & 0&0 \\ sin \gamma & cos \gamma & 0 &0 \\ 0 & 0 &1 &0\\ 0 &0&0&1 \end{bmatrix} \tag{绕Z轴变换矩阵} ⎣⎢⎢⎡cosγsinγ00−sinγcosγ0000100001⎦⎥⎥⎤(绕Z轴变换矩阵)
按照X、Y、Z的顺序,将上述三个矩阵相乘,即得到旋转矩阵:
(绕Z轴变换矩阵) [ c o s β ∗ c o s γ − c o s β ∗ s i n γ s i n β 0 s i n α ∗ s i n β ∗ c o s γ + c o s α ∗ s i n γ − s i n α ∗ s i n β ∗ s i n γ + c o s α ∗ c o s γ − s i n α ∗ c o s β 0 − c o s α ∗ s i n β ∗ c o s γ + s i n α ∗ s i n γ c o s α ∗ s i n β ∗ s i n γ + s i n α ∗ c o s γ c o s α ∗ c o s β 0 0 0 0 1 ] \begin{bmatrix} cos \beta*cos\gamma & -cos\beta*sin \gamma & sin\beta&0 \\ sin \alpha * sin\beta* cos \gamma + cos \alpha*sin\gamma& -sin \alpha * sin \beta * sin \gamma + cos \alpha *cos \gamma & -sin \alpha * cos \beta & 0 \\ -cos \alpha * sin \beta* cos \gamma + sin \alpha*sin \gamma & cos \alpha * sin \beta * sin \gamma + sin \alpha * cos \gamma &cos \alpha * cos \beta &0\\ 0 &0&0&1 \end{bmatrix} \tag{绕Z轴变换矩阵} ⎣⎢⎢⎡cosβ∗cosγsinα∗sinβ∗cosγ+cosα∗sinγ−cosα∗sinβ∗cosγ+sinα∗sinγ0−cosβ∗sinγ−sinα∗sinβ∗sinγ+cosα∗cosγcosα∗sinβ∗sinγ+sinα∗cosγ0sinβ−sinα∗cosβcosα∗cosβ00001⎦⎥⎥⎤(绕Z轴变换矩阵)
平移、缩放、旋转的矩阵计算实现如下:
Matrix& Matrix::scale(float x, float y, float z) {
Matrix temp;
temp[M00] = x;
temp[M11] = y;
temp[M22] = z;
*this *= temp;
return *this;
}
Matrix& Matrix::scale(float scale) {
return this->scale(scale,scale,scale);
}
Matrix& Matrix::translate(float x, float y, float z) {
Matrix temp;
temp[M03] = x;
temp[M13] = y;
temp[M23] = z;
*this *= temp;
return *this;
}
Matrix& Matrix::rotate(float x, float y, float z) {
Matrix temp;
auto M_PI_180 = (float) (M_PI / 180.0f);
x *= M_PI_180;
y *= M_PI_180;
z *= M_PI_180;
float cx = cosf(x);
float sx = sinf(x);
float cy = cosf(y);
float sy = sinf(y);
float cz = cosf(z);
float sz = sinf(z);
float cx_sy = cx * sy;
float sx_sy = sx * sy;
temp[M00] = cy * cz;
temp[M10] = -cy * sz;
temp[M20] = sy;
temp[M01] = sx_sy * cz + cx * sz;
temp[M11] = -sx_sy * sz + cx * cz;
temp[M21] = -sx * cy;
temp[M02] = -cx_sy * cz + sx * sz;
temp[M12] = cx_sy * sz + sx * cz;
temp[M22] = cx * cy;
*this *= temp;
return *this;
}
View矩阵
上面提到,View矩阵,代表的是相机的外参,包括相机的位置、相机镜头的朝向以及相机的上方向,比如你横着拿相机、或者竖着拿相机,改变的就是相机的上方向。无论是相机的位置、相机的镜头朝向还是相机的上方向发生改变,相机预览的屏幕上显示出来的画面一定会有所改变。
实际上改变view的改变,是相机相对模型世界的改变,也就是说,改变view的参数,都可以通过改变model来达到同样的效果。比如相对一个模型来说,把相机靠近模型2个单位长度,和把模型靠近相机2个单位长度,最终模型在相机上呈现的效果是一样的。镜头的朝向及相机上方向的修改也是一样,model可以逆向操作,得到同样的呈现结果。
View矩阵的作用是将模型从模型世界坐标系中,转换到相对相机的观察坐标系中。常见的view矩阵的生成参数有两种,一种是三个参数,相机位置eye、目标位置position、相机上方向up。另外一种是相机位置、镜头方向、相机上方向。第一种参数,在计算过程中也会先转换成第二种参数,相机位置及目标位置就可以表示出相机镜头的方向。
而我们要生成一个View矩阵,实际上是要利用上面的参数,构建出一个以相机为中心的笛卡尔右手坐标系,然后将模型从原来的坐标系中转换到这个新的坐标系中来。处理过程主要如下:
1. 构建出相机空间的笛卡尔右手坐标系
- 获取相机镜头方向forward向量并归一化,它是Z轴,记为N。
- 利用相机镜头方向forward向量与相机上方向up向量,叉乘得出side向量并归一化,它是X轴方向,记为U。
- 利用U向量和N向量进行叉乘,重新计算出up向量并归一化,保证三轴一定相互垂直。记此向量为V。
- 完成以上三步后,得到的是一个左手坐标系,将向量N取,即可得到一个右手坐标系。
2. 求世界坐标到相机空间坐标的变换矩阵
想要从世界坐标到相机空间坐标,一般需要做两步变换:
- 旋转世界坐标,使世界坐标和相机空间坐标三轴方向一致,我们把这个旋转矩阵记作R.
将世界坐标矩阵看做是一个向量空间,对于这个向量空间, X轴单位向量X(1,0,0)、Y轴单位向量Y(0,1,0)和Z轴单位向量Z(0,0,1)可以看做是这个向量空间的基。而构建出的相机空间坐标的三个单位向量,显然也可以看做是这个向量空间的基。从世界坐标到相机空间坐标的变换,实际上就是基变换,求基变换的过度矩阵。从X、Y、Z基到U、V、N的基变换,很明显有:
U ⃗ = u x ∗ X ⃗ + u y ∗ Y ⃗ + u z ∗ Z ⃗ V ⃗ = v x ∗ X ⃗ + v y ∗ Y ⃗ + v z ∗ Z ⃗ N ⃗ = n x ∗ X ⃗ + n y ∗ Y ⃗ + n z ∗ Z ⃗ \vec{U} = u_x*\vec{X} + u_y*\vec{Y} + u_z*\vec{Z} \\ \vec{V} = v_x*\vec{X} + v_y*\vec{Y} + v_z*\vec{Z} \\ \vec{N} = n_x*\vec{X} + n_y*\vec{Y} + n_z*\vec{Z} U=ux∗X+uy∗Y+uz∗ZV=vx∗X+vy∗Y+vz∗ZN=nx∗X+ny∗Y+nz∗Z
所以,很明显可以得到一个R矩阵:
(旋转矩阵R) [ u x u y u z 0 v x v y v z 0 n x n y n z 0 0 0 0 1 ] \begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0\\ 0 &0&0&1 \end{bmatrix} \tag{旋转矩阵R} ⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎤(旋转矩阵R) - 平移旋转后的世界坐标,使其与相机空间坐标完全重合,我们把这个平移矩阵记作T,T的矩阵很明显就是:
(平移矩阵T) [ 1 0 0 − e y e x 0 1 0 − e y e y 0 0 1 − e y e z 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & -eye_x \\ 0 & 1 & 0 & -eye_y \\ 0 & 0 & 1 & -eye_z \\ 0 &0&0&1 \end{bmatrix} \tag{平移矩阵T} ⎣⎢⎢⎡100001000010−eyex−eyey−eyez1⎦⎥⎥⎤(平移矩阵T) - 最终要求的变换矩阵即为:M=R*T
(矩阵M) [ u x v x n x 0 u y v y n y 0 u z v z n z 0 − U ⃗ ⋅ e y e ⃗ − V ⃗ ⋅ e y e ⃗ − N ⃗ ⋅ e y e ⃗ 1 ] \begin{bmatrix} u_x & v_x & n_x & 0 \\ u_y & v_y & n_y & 0 \\ u_z & v_z & n_z & 0 \\ -\vec{U}\cdot\vec{eye} &-\vec{V}\cdot\vec{eye} &-\vec{N}\cdot\vec{eye}&1 \end{bmatrix} \tag{矩阵M} ⎣⎢⎢⎡uxuyuz−U⋅eyevxvyvz−V⋅eyenxnynz−N⋅eye0001⎦⎥⎥⎤(矩阵M)
Matrix Matrix::createViewMatrix(float posX, float posY, float posZ, float targetX, float targetY, float targetZ,
float upX, float upY, float upZ) {
Vec3f position(posX,posY,posZ);
Vec3f target(targetX,targetY,targetZ);
Vec3f up(upX,upY,upZ);
Vec3f N = (target - position).normalize();
Vec3f U = N.copy().cross(up).normalize();
Vec3f V = U.copy().cross(N).normalize();
N = -N;
Matrix mat;
mat[M00] = U.x;
mat[M01] = U.y;
mat[M02] = U.z;
mat[M10] = V.x;
mat[M11] = V.y;
mat[M12] = V.z;
mat[M20] = N.x;
mat[M21] = N.y;
mat[M22] = N.z;
mat[M03] = -U.dot(position);
mat[M13] = -V.dot(position);
mat[M23] = -N.dot(position);
return mat;
}
Projection投影
Projection矩阵即为投影矩阵,投影矩阵用于将相机空间的坐标点转换到裁剪坐标空间。而由始至终,我们计算用的三维坐标都是用齐次坐标,将转换到裁剪坐标空间的点,除以w分量以将齐次坐标转换位归一化设备坐标(NDC)。 裁减变换(视锥剔除) 的信息也隐含在投影矩阵中,这个操作一般是在将齐次坐标转换为归一化设备坐标前,将齐次坐标中的x、y、z分量分别入w分量比较,任意一个分量大于w或者小于-w,这个坐标点就不会被投影到设备屏幕上了。
常见的投影矩阵主要有两种,一种是正交投影,在正交投影下,最终投影的结果的大小和被投影物体与相机的距离无关。另外一种是透视投影,在透视投影下,被投影的物体投影的结果会呈现出近大远小的效果,即同样大的物体,距离相机越近,投影的结果越大。
正交投影
相对透视投影矩阵来说,正交投影矩阵的推导非常简单。正交投影一般有两个输入参数,分别位左边界l、右边界r、上边界t、下边界b、近平面n以及远平面f。假设经过模型空间的一点P(x,y,z),经过model和view矩阵变换后,得到了点P1(x1,y1,z1),P1经过了正交投影矩阵变换后,得到点P2(x2,y2,z2),点P2的xyz分量都应该在[-1,1]区间。P到P1的变换由Model和View矩阵决定,而P1到P2的变换由投影矩阵决定。
由正交投影的六个参数可以构成一个立方体,只有在立方体中的点,才会投影到屏幕上。而且很明显正交投影,点的x、y坐标是不会发生变换的(同一物体远处投影和近处投影,投影结果大小不变,也就是xy坐标不变)。
作出XOZ平面的投影如下(YOZ投影基本类似),从图中可以看出,如果P1点的X坐标确定,则无论Z轴如何变换,P2的X坐标也不会变换,对于Y坐标同样如此。也就是在正交投影下,P2的X坐标只和P1的X坐标相关,P2的Y坐标只与P1的Y坐标相关。
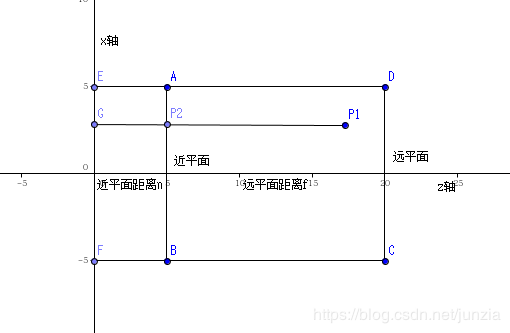
假设投影矩阵为:
(投影矩阵) [ a 00 a 10 a 20 a 30 a 01 a 11 a 21 a 31 a 02 a 12 a 22 a 32 a 03 a 13 a 23 a 33 ] \begin{bmatrix} a00 & a10 & a20 & a30 \\ a01 & a11 & a21 & a31 \\ a02 & a12 & a22 & a32 \\ a03 & a13 & a23 & a33 \end{bmatrix} \tag{投影矩阵} ⎣⎢⎢⎡a00a01a02a03a10a11a12a13a20a21a22a23a30a31a32a33⎦⎥⎥⎤(投影矩阵)
则应该有:
[ a 00 a 10 a 20 a 30 a 01 a 11 a 21 a 31 a 02 a 12 a 22 a 32 a 03 a 13 a 23 a 33 ] [ x 1 y 1 z 1 1 ] = [ x 2 y 2 z 2 w 2 ] = [ x 2 y 2 k 1 ] \begin{bmatrix} a00 & a10 & a20 & a30 \\ a01 & a11 & a21 & a31 \\ a02 & a12 & a22 & a32 \\ a03 & a13 & a23 & a33 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \\ z1 \\ 1 \end{bmatrix} = \begin{bmatrix} x2 \\ y2 \\ z2 \\ w2 \end{bmatrix} = \begin{bmatrix} x2 \\ y2 \\ k \\ 1 \end{bmatrix} ⎣⎢⎢⎡a00a01a02a03a10a11a12a13a20a21a22a23a30a31a32a33⎦⎥⎥⎤⎣⎢⎢⎡x1y1z11⎦⎥⎥⎤=⎣⎢⎢⎡x2y2z2w2⎦⎥⎥⎤=⎣⎢⎢⎡x2y2k1⎦⎥⎥⎤
展开即为:
(0) x 2 = a 00 ∗ x 1 + a 10 ∗ y 1 + a 20 ∗ z 1 + a 30 = a 00 ∗ x 1 + a 30 x2 = a00*x1+a10*y1+a20*z1+a30=a00*x1+a30 \tag{0} x2=a00∗x1+a10∗y1+a20∗z1+a30=a00∗x1+a30(0)
(1) y 2 = a 01 ∗ x 1 + a 11 ∗ y 1 + a 21 ∗ z 1 + a 31 = a 11 ∗ y 1 + a 31 y2 = a01*x1+a11*y1+a21*z1+a31=a11*y1+a31 \tag{1} y2=a01∗x1+a11∗y1+a21∗z1+a31=a11∗y1+a31(1)
(2) k = a 02 ∗ x 1 + a 12 ∗ y 1 + a 22 ∗ z 1 + a 32 = a 22 ∗ z 1 + a 32 k = a02*x1+a12*y1+a22*z1+a32=a22*z1+a32 \tag{2} k=a02∗x1+a12∗y1+a22∗z1+a32=a22∗z1+a32(2)
即有 a 10 = a 20 = a 01 = a 21 = a 02 = a 12 = a 03 = a 13 = a 23 = 0 a10=a20=a01=a21=a02=a12=a03=a13=a23=0 a10=a20=a01=a21=a02=a12=a03=a13=a23=0, a 33 = 1 a33=1 a33=1
而根据上面分析,P1应该在正交投影的六个参数构建的立方体中,即z1的取值范围应为[n,f]。而按照gl默认的设置,对应的k的范围应该位[-1,1](归一化设备坐标),当NDC不做任何设置时,其采用的是左手坐标系,所以对于公式(3)应该有:
a 22 ∗ n + a 32 = 1 a 22 ∗ f + a 32 = − 1 a22*n+a32 = 1 \\ a22*f+a32 = -1\\ a22∗n+a32=1a22∗f+a32=−1
求得 a 22 = 2 ( n − f ) a22 = \frac{2}{(n-f)} a22=(n−f)2 , a 23 = − n + f f − n a23 = -\frac{n+f}{f-n} a23=−f−nn+f。于此同理,根据x1和y1的取值范围 x 1 ∈ [ l , r ] x1\in[l,r] x1∈[l,r], y 1 ∈ [ b , t ] y1\in[b,t] y1∈[b,t],可以求得 a 00 = 2 ( r − l ) a00 = \frac{2}{(r-l)} a00=(r−l)2, a 11 = 2 ( t − b ) a11 = \frac{2}{(t-b)} a11=(t−b)2, a 30 = − r + l ( r − l ) a30 = -\frac{r+l}{(r-l)} a30=−(r−l)r+l, a 31 = − t + b ( t − b ) a31 = -\frac{t+b}{(t-b)} a31=−(t−b)t+b。即得到正交投影矩阵为:
(正交投影矩阵) [ 2 ( r − l ) 0 0 − r + l ( r − l ) 0 2 ( t − b ) 0 − t + b ( t − b ) 0 0 2 ( n − f ) − n + f f − n 0 0 0 1 ] . \begin{bmatrix} \frac{2}{(r-l)} & 0 & 0 & -\frac{r+l}{(r-l)} \\ 0 & \frac{2}{(t-b)} & 0 & -\frac{t+b}{(t-b)} \\ 0 & 0 & \frac{2}{(n-f)} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{bmatrix} .\tag{正交投影矩阵} ⎣⎢⎢⎢⎡(r−l)20000(t−b)20000(n−f)20−(r−l)r+l−(t−b)t+b−f−nn+f1⎦⎥⎥⎥⎤.(正交投影矩阵)
所以,代码实现如下:
Matrix Matrix::createOrthogonalCamera(float left, float right, float top, float bottom, float near, float far) {
Matrix mat;
mat[M00] = 2/(right-left);
mat[M11] = 2/(top - bottom);
mat[M22] = - 2/(far-near);
mat[M03] = - (left + right)/(right - left);
mat[M13] = - (top + bottom)/(top - bottom);
mat[M23] = - (near + far)/(far - near);
return mat;
}
透视投影
透视投影推导和正交投影有共通之处,和正交投影不同的是,透视投影下的物体,最终投影出来的结果会呈现出近大远小的效果。透视投影矩阵的输入参数一般是四个,广角fov(广角有fovx和fovy两种,本篇博客中采用fovx)、高宽比aspect、近平面near、远平面far。同透视投影一样,假设P(x,y,z)经过Model和View矩阵变换,得到P1(x1,y1,z1),然后经过透视投影矩阵变换,可以得到P2(x2,y2,z2),同正交投影一样,P2的xyz三个分量也都应该在[-1,1]区间,我们所需要关注的依旧是P1到P2的过程。
有透视投影矩阵的输入参数,可以构建出一个缺少顶部的金字塔的立体,这个就是透视投影的视锥,只有在视锥中的点才会投影到屏幕上。
和正交投影不同的是,透视投影下会有近大远小的效果,所以投影前后的x,y左边不再相同。构建出P1、P2及视锥图在XOZ平面下的投影图。从图中可以看出,一般情况下,当P1的Z坐标发生变化时,P2的X坐标也会发生变换。同样Y坐标也是如此。

则应该有:
t a n f o v 2 = w / 2 n , a s p e c t = h w 即 有 : w = 2 ∗ n ∗ t a n f o v 2 , h = 2 ∗ a s p e c t ∗ n ∗ t a n f o v 2 tan\frac{fov}{2} = \frac{w/2 }{n} ,aspect = \frac{h}{w}即有:w = 2*n*tan\frac{fov}{2},h = 2*aspect*n*tan\frac{fov}{2} tan2fov=nw/2,aspect=wh即有:w=2∗n∗tan2fov,h=2∗aspect∗n∗tan2fov
根据相似三角的性质,以及右手坐标系下,P1点应该在Z轴半轴范围中,故而有:
x 1 x 2 = y 1 y 2 = − z 1 n 其 中 : x 2 ∈ [ − w 2 , w 2 ] , y 2 ∈ [ − h 2 , h 2 ] \frac{x1}{x2} =\frac{y1}{y2} = -\frac{z1}{n} 其中:x2\in[-\frac{w}{2},\frac{w}{2}],y2\in[-\frac{h}{2},\frac{h}{2}] x2x1=y2y1=−nz1其中:x2∈[−2w,2w],y2∈[−2h,2h]
将P2所有的分量限定在 [ − 1 , 1 ] [-1,1] [−1,1]之间,则有:
x 2 = x 2 w / 2 = − n / z 1 ∗ x 1 n ∗ t a n ( f o v / 2 ) = − x 1 z 1 ∗ t a n ( f o v / 2 ) x_2 = \frac{x2}{w/2}=\frac{-n/z1*x1}{n*tan(fov/2)} = -\frac{x1}{z1*tan(fov/2)} x2=w/2x2=n∗tan(fov/2)−n/z1∗x1=−z1∗tan(fov/2)x1
y 2 = y 2 h / 2 = − n / z 1 ∗ y 1 n ∗ a s p e c t ∗ t a n ( f o v / 2 ) = − y 1 z 1 ∗ a s p e c t ∗ t a n ( f o v / 2 ) y_2 = \frac{y2}{h/2}=\frac{-n/z1*y1}{n*aspect*tan(fov/2)} = -\frac{y1}{z1*aspect*tan(fov/2)} y2=h/2y2=n∗aspect∗tan(fov/2)−n/z1∗y1=−z1∗aspect∗tan(fov/2)y1
也就是说,P2的坐标应该为:
P 2 ( − x 1 z 1 ∗ t a n ( f o v / 2 ) , − y 1 z 1 ∗ a s p e c t ∗ t a n ( f o v / 2 ) , z 2 ) P2(-\frac{x1}{z1*tan(fov/2)}, -\frac{y1}{z1*aspect*tan(fov/2)},z_2) P2(−z1∗tan(fov/2)x1,−z1∗aspect∗tan(fov/2)y1,z2)
在计算时,我们使用的齐次坐标进行计算,所以我们所期望得到的P2坐标其实是:
P 2 ( − t ∗ x 1 z 1 ∗ t a n ( f o v / 2 ) , − t ∗ y 1 z 1 ∗ a s p e c t ∗ t a n ( f o v / 2 ) , t ∗ z 2 , t ) 其 中 , t 为 任 意 非 零 值 P2(-t*\frac{x1}{z1*tan(fov/2)}, -t*\frac{y1}{z1*aspect*tan(fov/2)},t*z_2,t)其中,t为任意非零值 P2(−t∗z1∗tan(fov/2)x1,−t∗z1∗aspect∗tan(fov/2)y1,t∗z2,t)其中,t为任意非零值
由于上面P2的坐标表现形式,P2的X分量是由P1的X分量和Z分量构成,P2的Y分量是由P1的Y分量和Z分量构成,这样很难得逆推出一个合适的矩阵。我们需要消除掉P2坐标中两个P1分量在一起的情况,以便方便推出我们所需要的矩阵,所以我们将t取值为-z1。则P2坐标为:
P 2 ( x 1 t a n ( f o v / 2 ) , y 1 a s p e c t ∗ t a n ( f o v / 2 ) , − z 1 ∗ z 2 , − z 1 ) P2(\frac{x1}{tan(fov/2)}, \frac{y1}{aspect*tan(fov/2)},-z1*z_2,-z1) P2(tan(fov/2)x1,aspect∗tan(fov/2)y1,−z1∗z2,−z1)
依旧假设投影矩阵为:
(透视投影矩阵) [ a 00 a 10 a 20 a 30 a 01 a 11 a 21 a 31 a 02 a 12 a 22 a 32 a 03 a 13 a 23 a 33 ] \begin{bmatrix} a00 & a10 & a20 & a30 \\ a01 & a11 & a21 & a31 \\ a02 & a12 & a22 & a32 \\ a03 & a13 & a23 & a33 \end{bmatrix} \tag{透视投影矩阵} ⎣⎢⎢⎡a00a01a02a03a10a11a12a13a20a21a22a23a30a31a32a33⎦⎥⎥⎤(透视投影矩阵)
根据放射变换应该有:
[ a 00 a 10 a 20 a 30 a 01 a 11 a 21 a 31 a 02 a 12 a 22 a 32 a 03 a 13 a 23 a 33 ] [ x 1 y 1 z 1 1 ] = [ x 1 t a n ( f o v / 2 ) y 1 a s p e c t ∗ t a n ( f o v / 2 ) − z 1 ∗ z 2 − z 1 ] \begin{bmatrix} a00 & a10 & a20 & a30 \\ a01 & a11 & a21 & a31 \\ a02 & a12 & a22 & a32 \\ a03 & a13 & a23 & a33 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \\ z1 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{x1}{tan(fov/2)} \\ \frac{y1}{aspect*tan(fov/2)} \\ -z1*z_2 \\-z1 \end{bmatrix} ⎣⎢⎢⎡a00a01a02a03a10a11a12a13a20a21a22a23a30a31a32a33⎦⎥⎥⎤⎣⎢⎢⎡x1y1z11⎦⎥⎥⎤=⎣⎢⎢⎡tan(fov/2)x1aspect∗tan(fov/2)y1−z1∗z2−z1⎦⎥⎥⎤
既有: a 10 = a 20 = a 30 = a 01 = a 21 = a 31 = a 02 = a 12 = a 03 = a 13 = 0 , a 23 = − 1 , a 33 = 0 a10 = a20 = a30 = a01 = a21 = a31 = a02 = a12= a03 = a13=0,a23=-1,a33=0 a10=a20=a30=a01=a21=a31=a02=a12=a03=a13=0,a23=−1,a33=0 , a 00 = 1 t a n ( f o v / 2 ) a00=\frac{1}{tan(fov/2)} a00=tan(fov/2)1, a 11 = 1 a s p e c t ∗ t a n ( f o v / 2 ) a11 = \frac{1}{aspect*tan(fov/2)} a11=aspect∗tan(fov/2)1 (其中,a23和a33的推出是因为 a 23 ∗ z 1 + a 33 = − z 1 a23*z1 +a33 = -z1 a23∗z1+a33=−z1)
且有:
a 22 ∗ z 1 + a 32 = − z 1 ∗ z 2 a22*z1+a32 = -z1*z2 a22∗z1+a32=−z1∗z2
而对于上面的方程组,又已知z2取值范围位[-1,1],对应的z1的取值范围位[-n,-f],取两边的极限值,带入方程组,即为:
( − n ) ∗ a 22 + a 32 = − ( − 1 ) ∗ ( − n ) ( − f ) ∗ a 22 + a 32 = − 1 ∗ ( − f ) (-n)*a22 +a32 =- (-1)*(-n) \\ (-f)*a22+a32=-1*(-f) (−n)∗a22+a32=−(−1)∗(−n)(−f)∗a22+a32=−1∗(−f)
联立解得: a 22 = − f + n f − n , a 32 = 2 n f n − f a22=-\frac{f+n}{f-n},a32=\frac{2nf}{n-f} a22=−f−nf+n,a32=n−f2nf
即得到透视投影的矩阵为:
(透视投影矩阵) [ 1 t a n ( f o v / 2 ) 0 0 0 0 1 a s p e c t ∗ t a n ( f o v / 2 ) 0 0 0 0 − f + n f − n 2 n f n − f 0 0 − 1 0 ] . \begin{bmatrix} \frac{1}{tan(fov/2)} & 0 & 0 & 0 \\ 0 & \frac{1}{aspect*tan(fov/2)}& 0 & 0 \\ 0 & 0 &-\frac{f+n}{f-n} & \frac{2nf}{n-f} \\ 0 & 0 & -1 & 0 \end{bmatrix} .\tag{透视投影矩阵} ⎣⎢⎢⎢⎡tan(fov/2)10000aspect∗tan(fov/2)10000−f−nf+n−100n−f2nf0⎦⎥⎥⎥⎤.(透视投影矩阵)
Matrix Matrix::createPerspectiveCamera(float fov, float aspect, float near, float far) {
Matrix mat;
mat[M00] = 1/tanf(fov/2);
mat[M11] = 1/(aspect*tanf(fov/2));
mat[M22] = - (far + near) / (far - near);
mat[M32] = - 2 * far * near / (far - near);
mat[M23] = -1.0f;
mat[M33] = 0.0f;
return mat;
}
视口变换
前面经过一系列变换之后,我们将初始的世界空间的坐标点,转换成了NDC坐标(规范化设备坐标)。NDC坐标也是一个3D坐标,但是显然,我们的设备最终显示出来的基本都是2D的,所以从NDC坐标到2D坐标还有一个变换。在大多数时候,我们不需要做这一步,是因为我们只需要传递给gl_Position一个NDC坐标,OpenGL会帮我们把NDC坐标,转换成2D坐标,渲染到屏幕上,这个过程,我们可以称之为视口变换。
在OpenGL中,我们会调用glViewPort来进行视口变换,ViewPort不同,NDC最后转换成2D坐标的结果就不同。
NDC坐标和经过视口变换的坐标(屏幕坐标)成线性关系,其实主要是针对xy分量做线性映射,z分量保持不变。在经过投影变换,世界坐标转换成NDC坐标后,z分量已经无法影响到点投影到屏幕上的位置了,那么NDC坐标中为什么还要有z分量?因为世界空间是一个3D空间,物体离相机镜头有远有近,我们需要保留其z分量信息,以便于决定当n个点xy分量相同时,最终渲染到屏幕上的点,是离相机近的点,也就是做遮挡处理。
假设viewPort为(x,y,width,height),则视口变换的矩阵应该为:
(视口变换矩阵) [ w i d t h 2 0 0 w i d t h 2 + x 0 h e i g h t 2 0 h e i g h t 2 + y 0 0 1 0 0 0 0 1 ] . \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}+x \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} + y \\ 0 & 0 & 1 &0 \\ 0 & 0 & 0 & 1 \end{bmatrix} .\tag{视口变换矩阵} ⎣⎢⎢⎡2width00002height0000102width+x2height+y01⎦⎥⎥⎤.(视口变换矩阵)
也就是:
X s c r e e n = X n d c ∗ w i d t h 2 + w i d t h 2 + x Y s c r e e n = Y n d c ∗ h e i g h t 2 + h e i g h t 2 + y Z s c r e e n = Z n d c Xscreen = Xndc*\frac{width}{2}+\frac{width}{2}+x \\ Yscreen = Yndc*\frac{height}{2} + \frac{height}{2} + y \\ Zscreen = Zndc Xscreen=Xndc∗2width+2width+xYscreen=Yndc∗2height+2height+yZscreen=Zndc
所以,总的来说,从世界坐标转换到屏幕坐标,其变换过程为:
- MVP变换求投影空间坐标: P r o j P o i n t = W o r l d P o i n t ∗ M o d e l ∗ V i e w ∗ P r o j e c t ProjPoint = WorldPoint*Model*View*Project ProjPoint=WorldPoint∗Model∗View∗Project
- 由投影空间坐标求NDC坐标: N D C P o i n t ( x , y , z , w ) = P r o j P o i n t ( x w , y w , z w , 1 ) NDCPoint(x,y,z,w) = ProjPoint(\frac{x}{w},\frac{y}{w},\frac{z}{w},1) NDCPoint(x,y,z,w)=ProjPoint(wx,wy,wz,1)
- 由NDC坐标转空间坐标:
S c r e e n P o i n t ( x , y , z ) = N D C P o i n t ( w i d t h 2 ∗ x + w i d t h 2 + l e f t , h e i g h t 2 ∗ y + h e i g h t 2 + t o p , z ) ScreenPoint(x,y,z) = NDCPoint(\frac{width}{2}*x+\frac{width}{2}+left,\frac{height}{2}*y + \frac{height}{2} + top,z) ScreenPoint(x,y,z)=NDCPoint(2width∗x+2width+left,2height∗y+2height+top,z)
源码
Matrix实现及使用示例源码托管在Github上,欢迎Fork和Star——Charm项目源码
欢迎转载,转载请保留文章出处。湖广午王的博客[http://blog.csdn.net/junzia/article/details/85939783]