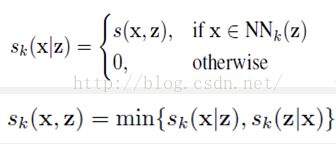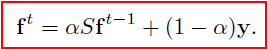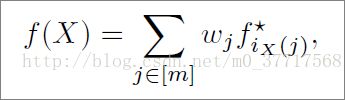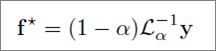Efficient Diffusion on Region Manifolds Recovering Small Objects with Compact CNN Representations

        这篇论文《Efficient Diffusion on Region Manifolds: Recovering Small Objects with Compact CNN Representations》发表在2017年CVPR上。

        我自己的PPT: Efficient Diffusion on Region Manifolds: Recovering Small Objects with Compact CNN Representations 

        对于文章题目《在区域流形上的有效扩散：使用紧凑的CNN表示恢复小目标》，重点理解了在区域流形上的有效扩散过程。恢复小目标部分还不是很明白是如何进行的。

        博客内容的顺序与论文稍有不同。

        1. 背景知识介绍

        阅读这篇文章之前，从未接触过所谓流形以及扩散的概念。所以找了一些文献，先简单解释一下这两个名词。

        流形(Manifold)是现代数学中描述复杂对象的基本概念，是指局部地具有n维空间或某个其他向量空间的结构(拓扑的、光滑的、同调的等等)的几何对象。粗略地讲，流形就是将局部简单的面片粘合起来形成整体复杂的形状。

    虽然概念给出，但依然不好理解。

    在一篇中文文献中提到流形可以应用在图像分类问题中：“在分类问题中，如果每类样本均能够由一个流形很好地描述，那么我们只需要对每类样本学习一个流形，在分类时计算样本到每个流形的距离，将其分类到与其最近的流形所在的类即可。”

        基于这句话，我认为流形可以简单地理解为是一个类的模板或者一个类的图像的聚类结果。对图像提取特征，每一类的图像描述符形成一个流形。

         扩散：类似个性化的PageRank

        个性化的PageRank的目标是要计算所有节点相对于用户u的相关度。从用户u对应的节点开始游走，从当前节点指向的节点中按照均匀分布随机选择一个节点往下游走。经过很多轮游走之后，每个顶点被访问到的概率也会收敛趋于稳定，这个时候我们就可以用概率来进行排名了。

    可以看出，个性化的PageRank可以得到其他节点相对于查询的相关度（相似性）。所以可以应用在图像检索中。

    扩散：离线构建某数据集的领域图。查询时，使用领域图在流形上扩散，得到每个节点相对于查询的ranking score。

    为什么采用这种方式，而不是普通的计算欧氏距离等方法直接去排名呢？在经典文章《Ranking on data manifolds》中是这样解释的：

   

    如上图所示，两个半月形代表两个流形。当查询query时，使用欧氏距离的排名结果如第二张图所示，而我们理想的、根据流形的定义应该得到第三张图的排名结果（同类或者相似的点应该在同一个流形上）。可见，在流形上扩散单单使用欧氏距离等是不合适的。

    在《Ranking on data manifolds》中，提到了一种经典的在流形上扩散的机制：

    A. 计算相似性矩阵

    将数据集中的图像提取特征，表示为。

    计算两两相似性，得到相似性矩阵。其中，。在实验中，核函数取。

    相似性矩阵A实际上就是领域图的邻接矩阵。

    接下来对A进行归一化：其中D为A的度矩阵。D是对角矩阵，其对角元素分别为A的各行元素之和。

    B. 为了去除一些噪声和外点的影响，增加局部约束

    这两个式子的物理意义是，当且仅当x和z两个节点之间互为k邻居时，在领域图中才有连线，且连线的权重为较小的那个值。

    C. 扩散

    首先定义一个指示向量y，若xi是query，则yi置1，否则yi置0。

    扩散的目标就是每个节点都有一个相对于查询的ranking score。用f表示。

    在文章中，f 利用迭代得到。在这里不讨论得到这个迭代公式的过程。

    实验时，常数取0.99。

    2. 方法及实验

    因为涉及到很多比较的内容。所以将方法和对应的对比实验放在一起，以防单独列出实验部分会混乱。

    以上所述的过程中，流形上的每一个point指代的是一张图的特征。在本文中，作者将这种整幅图的扩散改进为区域的扩散。

    我所理解的区域扩散为何有效：假设想要检索一张包括猫和狗的图像，如果能分别检索猫和狗，其效果一定比只对图像提取全局特征进行检索好。

    对于每一张图，使用R-MAC方法，平均提取21个regions。query也同样处理，其所有的region记为Q。

    提取每个region的特征，计算regions间的邻域图，从而进行区域的扩散。

    改为区域扩散之后，扩散的结果是每个region相对于query的每个region得到一个ranking score。而在图像检索任务中，最后仍然需要得到某一张图对于query整张图的ranking score。所以很自然地，此时需要一个函数：

    这个公式很简单，就是属于某一张图的所有region的ranking score的加权求和。

    作者比较了两种情况：

           a. sum pooling：权重均为1

           b. generalized max-pooling (GMP): 权重为：

 

    该公式来自于论文《Generalized max-pooling》。 

    比较发现GMP在所有数据集上均得到比sum pooling更好的结果：

    

     

     至此，区域扩散的方法部分解释完毕。除此之外，作者加了很多优化的方法：

     A.处理新的query

      在图像检索任务中，大部分都是假设query来自于数据集，也就是query的特征存在在A中。然而实际上，query可能不在数据集中。在这种情况下，在改变指示向量y的同时，需要对相似性矩阵进行更改。这样的计算量就会很大。作者提出，可以使用query的k邻居进行替代检索。

  

       由此得到的y，使最大的k个值保持不变，其他置为0，就可以达到找到query的k邻居的目的。之后就可以去进行迭代求解了。

         B.  共轭梯度法

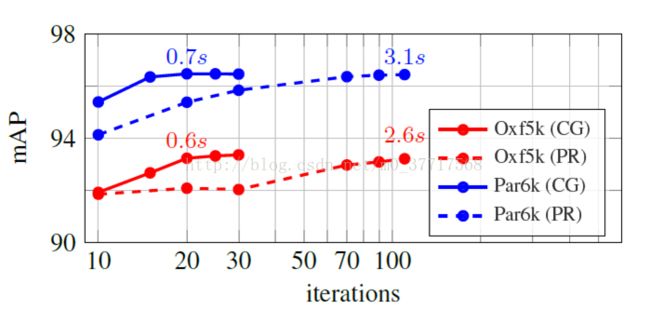
              解迭代公式f 时，迭代速度会很慢，作者提出可以用共轭梯度法求解：

              作者进行了实验，发现共轭梯度法（CG）的收敛速度很快，而且准确率不受影响。

                

          C. 大数据下的处理

              a. 紧凑的CNN表示

                  大数据下，每张图提取的region应在保证准确率的情况下越少越好 ，采用方法： 高斯混合模型（GMM）

                  实验发现，使用GMM，每张图只提取5个region即可在时间和准确率间取得一个很好的平衡。

              b. 构建邻域图

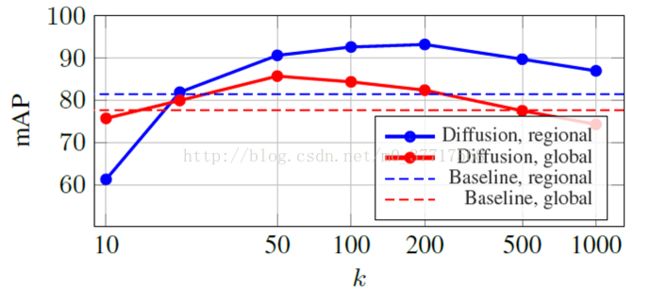
                  若完全的计算相似性矩阵，并去构建邻域图计算量会很大。因为作者采用论文《Efficientk-nearest neighbor graph construction for generic similarity measures》中提出的k-NN graph construction method 

                  首先确定参数k，然后进行构建邻域图的时间以及检索的准确率对比。发现该方法在稍微降低准确率的情况下，很大程度地减少检索时间。

              c. 截断相似性矩阵

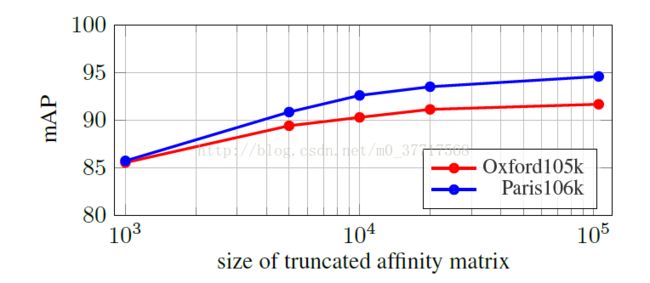
                  很明显，如果将区域扩散应用在每张图上，计算量会很大。因为先用全局特征确定排名靠前的图像，接着仅对这些图像进行区域扩散，并在相似性矩阵中只保留相应的行和列。

                  实验发现，准确率随进行区域扩散的图像数量增加而增加。只对前十分之一的图像进行区域扩散可以认为准确率不错。

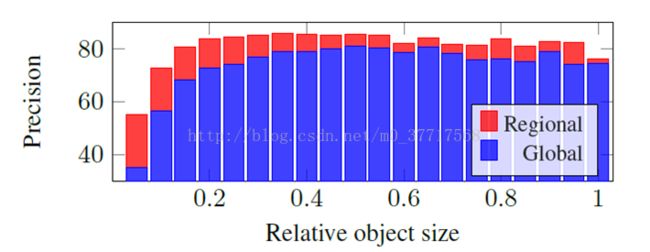
          最后，作者观察了区域扩散对小目标的检索效果。发现能很显著地增加小目标图像的检索准确率。