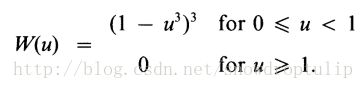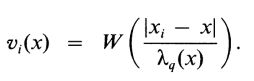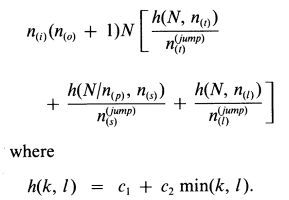STL——以鲁棒局部加权回归作为平滑方法的时间序列分解方法
摘要
STL是一种把时间序列分解为趋势项(trend component)、季节项(seasonal component)和余项(remainder component)的过滤过程。
STL有一个简单的设计,它包含了loess平滑法的一系列应用;这个简单的设计允许对过程的属性进行分析,也可以实现快速计算,即使对于长时间的时间序列、以及大量的趋势和季节性的平滑,也可以进行快速计算。
STL的其它特点是:
1. 关于季节性和趋势平滑的量,这是一种几乎连续的方式,从非常少量的平滑到非常大量的平滑;
2. 稳健的估计趋势项和季节项,而不会被数据中的异常行为扭曲;
3. 可以指定季节项的周期为采样时间间隔任意大于一的整数倍;
4. 可以分解有缺失值的时间序列;
关键词:季节调整;时间序列;loess
序言
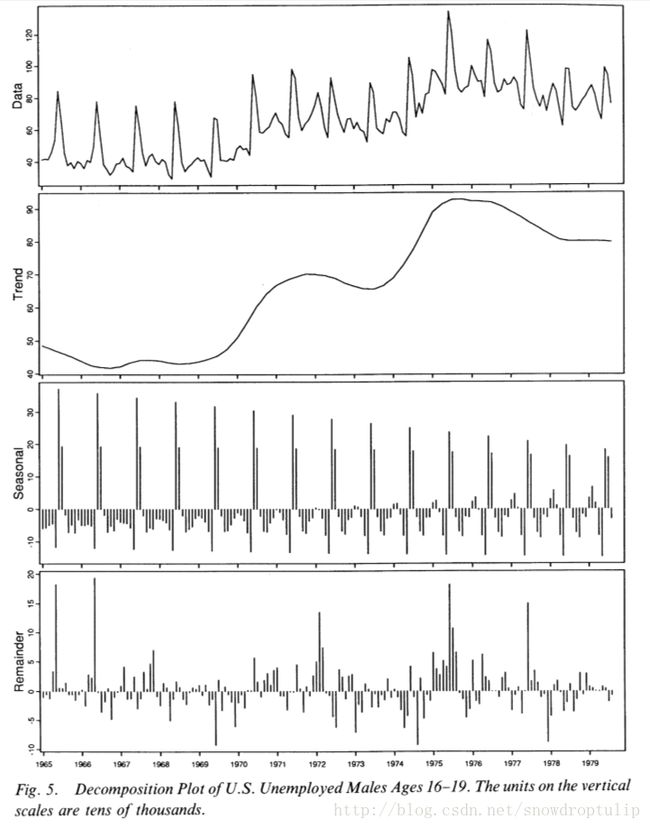
STL是一种把时间序列分解为三个部分:趋势项(trend component)、季节项(seasonalcomponent)和余项(remainder component)的过滤程序。图1是一个示例:
第一个面板是夏威夷的茂纳罗亚太阳天文台观测到的每一天大气中二氧化碳的平均测量值,
第二个面板是趋势项:数据的低频变化,同时在水平方向上市非平稳,长期的变化;
第三个面板是季节项:频率的变化是或者接近季节频率,在本示例中周期是一年。
第四个面板是余项:是除了季节性和趋势项的变化。
假定分别用Yv, Tv,Sv,Rv分别代表数据,趋势项、季节项和余项,v的范围为0到N,那么Yv = Tv+ Sv+Rv
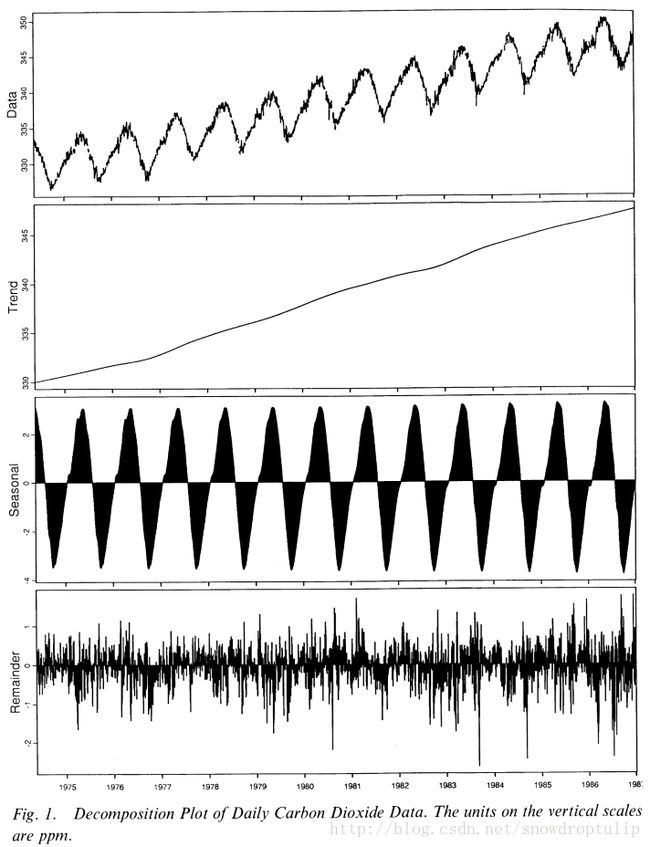
图1是由作为世界政府项目监控二氧化碳的浓度的一部分的美国国家海洋和大气管理局(NOAA)测量的。测量的时间跨度为1974年4月12号到1986年12月31日。我们删除了所有的2月29日,假定2月29日不存在,目的是为了使一个周期等于365天;所以删掉了2月29号的数据,跨度为4609天。在这4609天中,有416天的数据是缺失的,所以总共有4193个二氧化碳测量值。
我们STL的目标是开发一个分解过程和一个计算机实现工具,使其满足如下相互依赖的条件:
1. 简单的设计和简单的使用方式;
2. 灵活的指定趋势项和季节项的变量个数;
3. 指定季节项一个周期的观察数量为任意大于一的整数;
4. 分解有缺失值的时间序列的能力;
5. 趋势项和季节项的稳健性,不会被数据中短暂的异常行为扭曲数据;
6. 简单的计算实现,以及快速计算能力,甚至对于长时间的时间序列可以快速计算。
STL由一系列平滑操作组成,每一个平滑操作都有例外,STL使用同样的平滑器:局部权重回归,或者loess。在第二章,我们将会讨论loess,然后给出STL的过渡。
数据据分析师在做STL在的时候有许多参数必须设定。在第三章,讨论了如何设定它们。对于一些参数,可以使用预先设定的值,但是对于另外一些参数的设定必须根据数据的属性来设定;文章将会给出一些诊断方法来帮助数据分析师做这些决策;
计算是一个关键的因素。为了达到尽可能广泛的适用范围,计算机程序实现季节趋势的分解过程必须很快,甚至对于图1的长时间的时间序列也必须很快实现,并且计算机程序应该有简单,模块化的结构。第四章讨论了STL的实现。
STL的设计和实际中参数的设定都是基于时间序列变量一部分变为季节项另一部分变为趋势项的理解。这个理解来自于第五章中特征值和频率响应分析。
第六章对以下的一些主题展开了讨论:实际中STL参数选择的总结;STL重要特征的回顾;用两个例子展现了STL的设计可以得到易于修改易于到达其它目标;把STL和一个时间序列模型结合,得到置信区间;与X-11的对比;如何获取实现STL公共的Fortran代码
第二章、STL的定义
在这章,我们将会讨论Loess平滑法和STL操作。我们的目的是给出细节的简单的描述;各方面的理由将在后面的章节给出
2.1 Loess
假设xi和yi分别(i = 1 to n)是自变量和因变量。Loess(locally weighted regression,局部加权回归)回归曲线,g(x),相当于是对于x,y的一个平滑,g(x)对于任何自变量都可以计算。这就意味着,loess回归不仅仅只能计算xi;正如我们所见,这是一个STL一个重要的特征——可以直接处理缺失值和对季节性去趋势化。事实上,loess可以作为一个函数,这个函数可以对任意的自变量来平滑y,但是对于STL,只需要一个独立变量。
g(x)的计算方法如下:对于一个正整数q,目前假设q小于n,q值代表与x最接近的q个点,并且每一个点xi根据它与x的距离给出一个邻近权重。假设λq(x)指的是xi距离x第q个远的距离。让W等于三次方的方程:
xi的邻近权重为:
现在我们假设q>n。λn(x)是xi与x最远的距离。对于q>n,我们定义λq(x)
然后我们像之前一样使用λq(x)定义邻近变量。
使用loess,d和q必须被定义。在STL中如何选择d和q将会在第3章中详细讨论。随着q的增加,g(x)变得越来越平滑。q趋向于无限大的时候,vi(x)趋向于零,并且g(x)趋向于一个d元普通最小二乘多项式的拟合。如果数据的潜在模式有缓慢的弯曲,那么d=1是合理的。但是如果有大量的弯曲,例如有很多峰和谷,那么d=2是个更好的选择。
假设每一个观察(xi, yi)有权重ρi,代表观察值相对于其它观察值的可靠性。例如,如果yi的方差为σ2ki,ki已知,那么ρi为1/ki。我们可以把这些权重合并在loess平滑中,使用一个简单的方法:使用ρivi(x)作为局部最小二成的拟合。我们将会看到,这些提供了简单的在STL中实现稳健性的机制。
2.2 总体设计:内循环和外循环
STL由两个循环机制组成,一个内循环嵌套在一个外循环里。每一次内循环,季节项和趋势项都会被更新一次;内循环的每个完整运行都由n(i)个这样的过程组成;每一个外循环通道都由内循环组成,可以计算得到稳健的权重;这些权重会用在下一个内循环中,用于减少趋势项和季节项中短暂的异常行为。第一次外循环设置的鲁棒权重都等于1,然后进行n(o)次外循环。n(i)和n(o)如何选择会在第三章中讨论。图1中的分解,n(i)=1,n(o)=10.
假设每一个周期的观察数——季节项的观察数为n(p)。例如,如果时间序列一年中每个月的时间序列,那么n(p)=12。我们需要参考季节循环中每一个点子序列的值。例如,对于一个按月的时间序列,n(p)=12,第一个子序列是一月份的值,第二个是二月份的值,以此类推,我们将会把每一个n(p)子序列是周期子序列(cycle-subseries)。
2.3 内循环
每一次内循环的过程由季节平滑组成,季节平滑指的是季节项的更新,紧跟着趋势项的平滑和更新。假设Sv(k)和Tv(k)(v=1 to n)是第k次迭代后的季节项和趋势项;这两项在所有的时间点都是有定义的,即使Yv是缺失的。那么第(k+1)次迭代,Sv(k+1)和Tv(k+1)的计算方法如下:
第一步:去趋势化(Detrending)。一个去趋势化的序列Yv- Tv(k)被计算。如果Yv在一些特定的点缺失的,那么,去趋势化的序列在这个缺失的点也同样会缺失。
第二步:周期子序列平滑(Cycle-subseries Smoothing)。每一个去趋势化的周期子序列都由q=n(s)和d=1的loess平滑。每一个时间点都计算了平滑值,包括缺失点,以及序列第一个时间点前的值和最后一个时间点后的值。例如,假设时间序列是按月的,n(p)=12,所以一月份的子序列的范围是从1943年1月份到1985年1月份,包括缺失的1960年一月份;然后平滑后的值在1942年1月份到1986年1月份都被计算了。所有子序列的平滑后的值是临时季节序列,cv(k+1),由N+2n(p)个值组成,v从- n(p)+1到N+ n(p).对于图1的分解,n(s)=35,如何选择将在第3章和第5章讨论。
第三步:平滑周期子序列的低通滤波(Low-Pass Filtering of SmoothedCycle-Subseries)。一个低通滤波被应用到cv(k+1)上。这个滤波由移动平均长度n(p)组成,接着是另一个移动平均长度n(p),接着一个移动平均长度3,然后由d=1和q=n(l)的loess平滑。n(l)如何选择将会在第三章和第五章讨论。对于图1的分解,n(l)=365。输出Lv(k+1)在时间点v=1到N是有定义的,因为这三个移动平均不能趋向于尽头;n(p)点在每一个结尾都会被遗失。预料到这个遗失,所以第二步的季节平滑在每次结束后都被扩展了n(p)个位置
第四步:平滑周期子序列的去趋势(Detrending of SmoothedCycle-Subseries)。季节项从第k+1迭代开始变为Sv(k+1)=Cv(k+1)- Lv(k+1)(v=1to N), Lv(k+1)时被减去,目的是防止低频影响进入季节项
第五步:去季节性(Deseasonalizing)。一个去季节性的序列Yv-Sv(k+1)被计算。如果Yv在特定的时间点缺失,那么去季节序列在这个点同样缺失。
第六步:趋势平滑(Trend Smoothing):去季节性的序列进行q=n(t)和d=1的loess平滑。平滑后的值在每一个时间点都存在,即使这些点观察值缺失。季节项在第k+1迭代时,Tv(k+1)(v=1to N)为平滑后的值。对于图1,n(t)=537.如何选择n(t)将会在第3章和第5章讨论。
因此内循环中第2,3,4步时季节平滑,第6步是趋势平滑
为了在第一次迭代的时候执行第一步,我们需要趋势项的初始值Tv(0)。使Tv(0)恒等于0效果非常好。趋势变成了周期子序列的一部分,cv(1),但是在第4步去趋势化中都被删除了。
2.4 外循环
假设我们最执行初次内循环后得到趋势项Tv和季节项Sv的估计值,那么余项等于
Rv= Yv – Tv - Sv
(注意:与Tv和Sv不一样,当Yv缺失的时候,余项Rv没有定义) 我们将会对每一个观察点Yv定义一个权重。稳健权重反应了Rv的极端性。数据中的异常值指的是非常大的|Rv|,这种情况下权重很小的或者为0,使
h = 6 median(|Rv|)
那么时间点v的稳健权重为ρv=B(|Rv|h),B是一个二次函数:
现在内循环被重复,但是在第二步(周期子序列平滑)和第六步(趋势平滑)的平滑中,时间v的邻近权重与鲁棒性权重ρv相乘。这是在2.1中讨论的合理权重。这些稳健性迭代由n(o)次外循环得到。每一次我们在输入内循环在初始运行时,我们不设置Tv(0)恒等于0,而是更倾向于上一次内循环的第六步的趋势项。
2.5 季节Post平滑
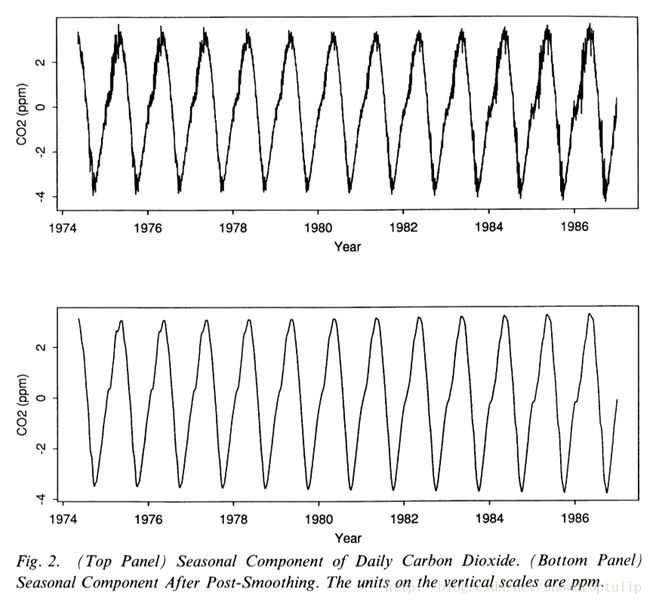
考虑图1每天的二氧化碳序列,STL的第二步——计算季节项基础的一步,有如下形式:365个去趋势化的周期序列分别被平滑然后放到一起形成临时的季节项。这意味着季节的每一个周期子序列将会跨年的被平滑。例如, 6月4号季节项的值从一年到下一年平滑的改变。但是平滑不允许季节项从一天到下一天的平滑。这种平滑不被允许的原因是,有许多时间序列是不适当的。图2的第一个面板显示了STL计算的每一天二氧化碳的季节项;有明显的局部稳健性。但是对于这个序列,我们希望得到一个一天到另一天平滑的一个项。
一个解决局部不平滑季节性的简单的方法是post平滑,post平滑是指用loess平滑STL得到的季节项。平滑后的值是最终的季节项。执行这个平滑的时候我们希望确认使用局部二次拟合,因为季节项中有许多峰值和谷值。我们同样不需要loess稳健性迭代,如果STL在局部稳健性中产生了一个表现很好的项。最终,q通常比较小或者比较适中,因为稳健性通常有一个比较小的方差。对于二氧化碳的数据,使用q=51来做post平滑。最终的季节项在图2第二面板中显示;这是图1中的一部分。
第三章、选择STL参数
STL有6个参数
n(p)= 每一个季节项周期中观察点的数量
n(i)= 内循环的次数
n(o)= 外循环鲁棒性迭代的次数
n(l)= 低通滤波的平滑参数
n(t)= 趋势项的平滑参数
n(s)= 季节项的平滑参数
选择前五个参数是简单的,但是对于最后一个参数n(s),对于每一个应用都必须小心的调整;我们提供了许多诊断方法来帮助做这些,在本章我们将会讨论如何选择。
3.1 斯科利普斯二氧化碳和失业男性
我们在这节将会使用两个时间序列当做示例。
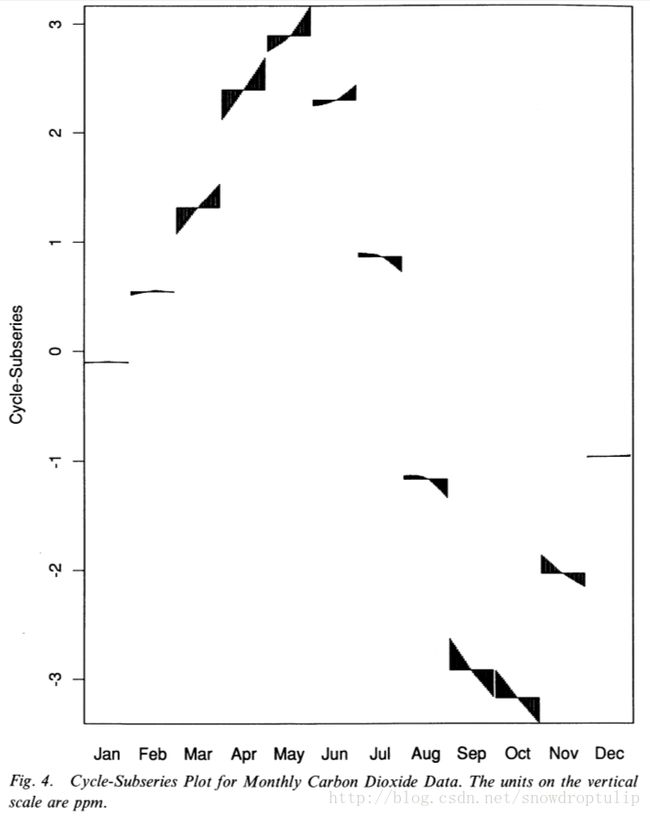
第一个示例是大气中每个月二氧化碳测量的平均值,由夏威夷的茂纳罗亚太阳天文台的海洋地球学斯克里普提供(Keeling, Bacastow, and Whorf1982)。图3的分解图显示了原始数据和三个分解项,数据从1959年1月到1987年12月;所有观察点的数据都存在,Carbon Dioxide Information Analysis Center ofthe Oak Ridge National Laboratory组织执行出了时间序列的结果。因为是年周期,所以n(p)=12.其他分解的参数为n(i)= 2, n(o) = 0, n(l)= 13, n(t) = 19并且n(s) = 35。图4是季节项的一个周期子序列图,每一个周期子序列根据时间都被分开画了。先画1月份的值,再画2月份的值,以此类推。该值的平均值由水平线描绘,而数值由水平线发出的垂直线的末端所描绘。
第二个时间序列是UM16,是美国从1965年1月到1979年8月16岁到19岁事业的男性人数。我们使用这样的时间数据,是因为这样读者可以比较我们之间讨论的二氧化碳数据。图5展示的是分解的图,图6展示的是周期子图。因为是一年周期,所以n(p)=12.其他值为n(i)= 1, n(o) = 5, n(l)= 13, n(t) = 21并且n(s) = 17。
3.2 n(p), 每一个季节项周期中观察点的数量
参数从应用中很容易得到。例如,对于前面讨论的两个二氧化碳序列,一年周期,按天统计的n(p)=365,按月统计的n(p)=12。时间序列完全有可能有两个或者三个的周期项;例如,一个按天的序列可能有按周和按年的周期。在这种情况下我们可以使用STL从短周期项到长周期项来成功的估算项,估算每一个项,减去它,在剩余值里估算下一个项。
3.3 n(i)内循环的次数,n(o)稳健迭代的次数
当数据的先验知识或者诊断表明非高斯的行为导致极端、短暂的变化,需要进行STL鲁棒性估计。否则我们可以省略稳健性迭代,并且把n(o)设置为0。在这种情况下,STL没有外循环,只有内循环构成。在图3所示的按月的二氧化碳数据中,没有异常行为,所以n(o)可以被设置为0.对于图5中的事业男性,前两个5月份是异常值,所以使用稳健的STL;我们将会在稍后学习这种异常行为。
首先,假设我们不需要鲁棒性,我们想要设置n(i)大一点,这样可以使得趋势项和季节项收敛。但是由于一些原因,这个收敛会非常的快,在许多情况下,n(i)=1就可以满足收敛,但是我们建议n(i)=2,这样可以保证近乎收敛。
现在假设我们需要稳健迭代,我们想让n(o)很大,这样可以使得季节项和趋势项的稳健估计收敛。在做这个的时候,让n(i)=1有两个原因:第一个是前面给出的原因,内循环收敛的非常快;第二个当嵌套时,他与无约束优化的一般原则有关系。过于提纯内部循环来达到总体收敛是不值得的。当n(i)=1时,我们发现n(o)=5是一个非常安全的值,而当n(o)=10可以保证近乎收敛。在失业男性的数据中,n(o)设为5,经过5次迭代后收敛。然后,对于图1的二氧化碳数据,收敛比较慢,所以进行了10次迭代。
当然,我们可以开发一个收敛条件,当满足条件是停止迭代。在我们的研究中,我们使用如下的条件来判断收敛:假设Uv(k)和Uv(k+1)是连续的趋势项或者季节项的迭代,那么Uv(k)如果满足一下条件就可以认为是一个收敛项:
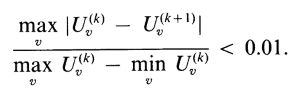
3.4 n(l),低通滤波的平滑参数
n(l)通常可以认定为大于或等于n(p)的最小奇数,原因会在第5章给出。这种n(l)的设定,这一选择有助于实现防止趋势和季节项在数据中出现相同变化,在文中所有的分解都有使用。图1中,n(l)=365,图3和图5,n(l)=13
3.5 n(s),季节平滑参数
随着n(s)的增加,每个周期子序列变得平滑。我们通常设定n(s)为奇数,原因将会在第5章给出,我们同时希望n(s)至少为7.
n(s)决定了构成季节项数据的变化。选择合适的变异取决于这个序列的特征。应该强调的是,季节变化的定义有一种内在的模糊性。数据分析师在选择季节平滑参数的时候定义了季节变化。我们将描述一种诊断方法,它可以帮助数据分析师选择定义;但是这些方法不能总是得到一个唯一的选择,许多应用的最终选择必须基于生成该机制的知识和分析的目标。所有季节分解过程都是不明确的,不仅仅是STL。Carlin和Dempster对这一点进行了透彻的讨论(1989)。
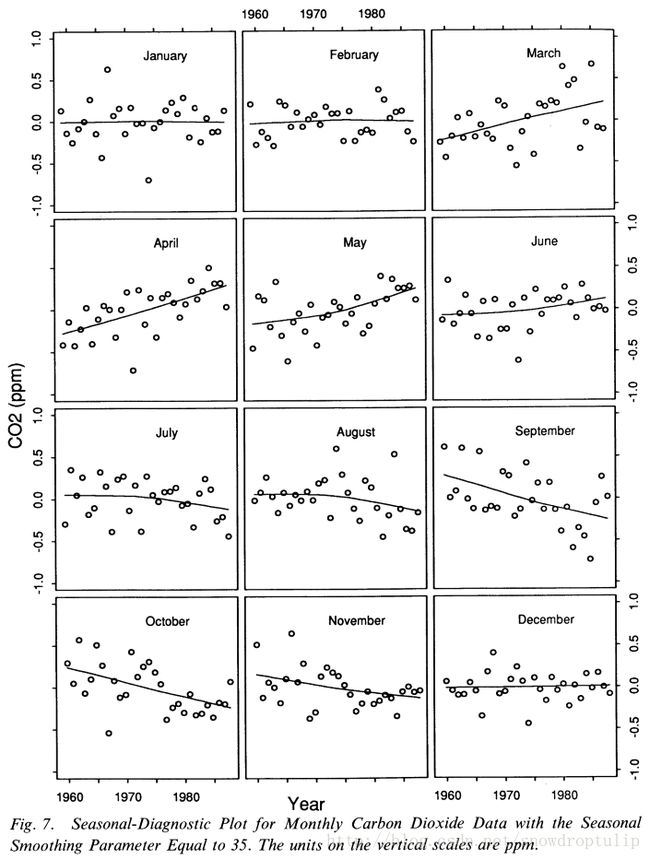
图7描述了一种诊断图形方法,可以帮助选择n(s)。图7中的每一个图形对每一个月份画了两组数据。令sk是第k个月季节项周期子序列的平均值,面板上第k个月的曲线减去了他们的平均值sk。圆点的值是季节项的k个周期子序列加上余项,同样是减去sk的。(减去sk的原因是将每个面板的中心设为0;注意面板的垂直比例尺都是相等的,所以我们可以通过比较不同面板的变化值)这种诊断方法,我们称为季节诊断图,帮助我们决定除了趋势化之外,有多少变量应该作为季节项,有多少应该作为余项。
图7画的值是当图3的n(s)=35时每个月二氧化碳的分解值。图8是n(s)下降为11时的季节诊断。每一个季节项的周期子序列明显是欠平滑的。与n(s)=35相比,季节值中增加的变化看起来是噪声,并不是有意义的季节变量,因为二氧化碳序列的周期主要是由北半球植被的周期影响的,所以我们期望一年是一个平滑的周期变化。
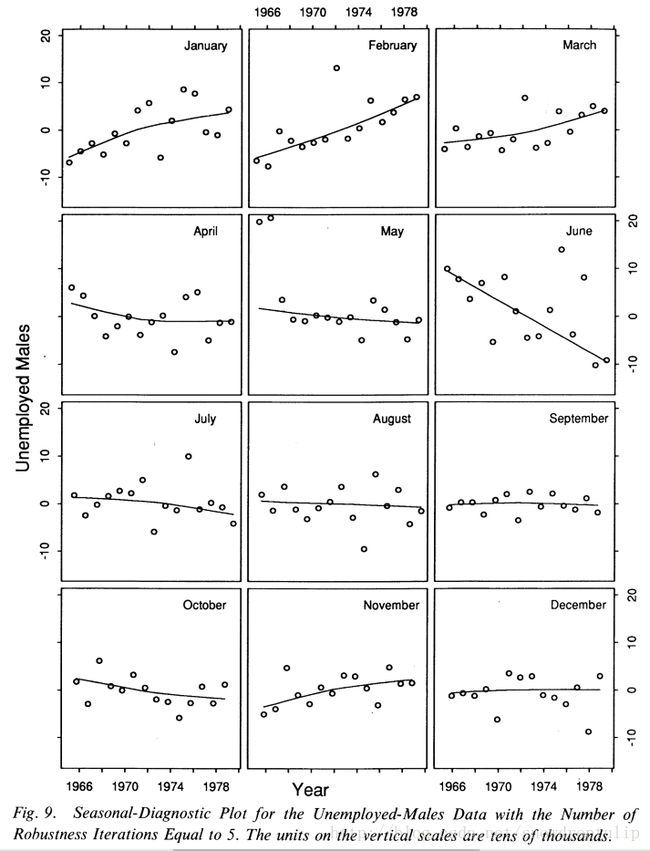
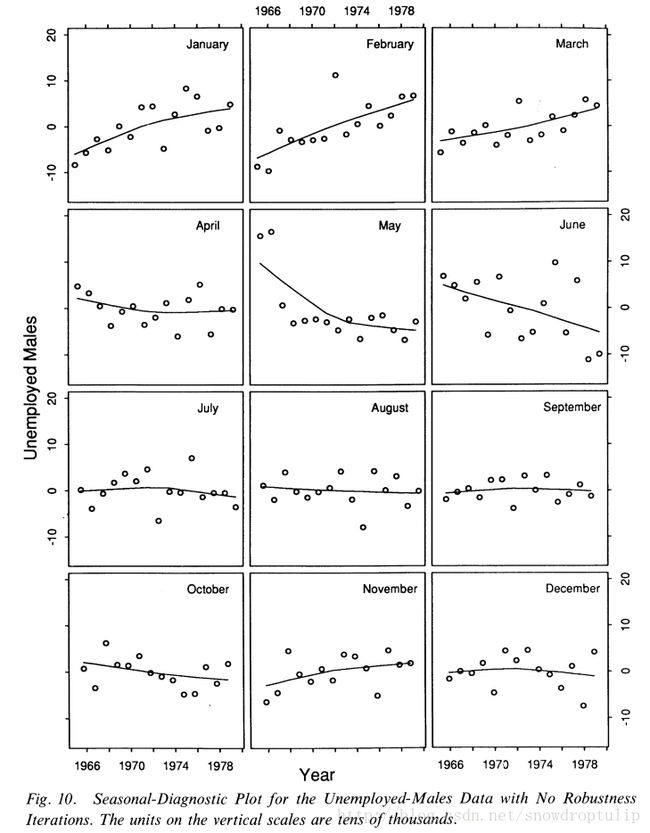
图9是n(s)=17时图5所示的失业男性鲁棒分解的季节诊断图,季节项的周期子序列似乎遵循了季节加余项的值得模式,而没有引入不适当的噪声。注意,五月份的季节项几乎是线性的,且遵循了主要值是Sv+Rv,而没有被初始的两个异常值扭曲。这就是稳健估计的结果。没有稳健性,季节项就会被扭曲。图10是一个没有使用鲁棒迭代进行分解的季节诊断示例图,参数是n(i)=2,n(o)=0,n(l)=13,n(t)=21,n(s)=17。季节项周期子序列的结果与其它分解的自周期序列相似,除了5月和6月,5月份中异常值扭曲了季节值;这些值既不考虑异常值,也不遵循剩余值得模式。(我们已经采取了五月份异常行为是一个短暂的现象的立场。如果有人对数据产生机制的详细信息了解的人有一个让人信服的论点,即行为是一种快速变化的季节性因素,那么我们会减小n(s)来解释季节性因素。)
3.6 趋势平滑参数 n(t)
随着n(t)的增加,趋势项Tv会从Xv中提取到更少的变化,也会变得更平滑。我们通常设定n(t)为奇数。
我们建议用如下的方法得到趋势项。把它看作是一个需要对季节进行估计的项,换言之,把STL的首要目标认为是季节项的估计。如果需要一个项来讨论数据中确切的低频变化,我们可以使用post趋势平滑。这意味着低滤波,比如loess,被应用在Tv+Rv上——移除季节项的数据,可以得到想要变化的项。正如我们所见,我们经常被迫做这些,因为n(t)的选择往往受到分解所需的限制,不能被选择,所以趋势项描述了数据中某个特定变化的部分。
趋势项在帮助估计季节项的时候有两个作用。第一个是移除永久的,长期的变化,例如图1和图3二氧化碳浓度永久的增加。如果我们不移除这些,季节项就会被扭曲。(这种行为的存在,阻止我们从一个普通数字滤波到以最基本的季节频率和它的谐波为中心的频带数据)。这种行为除非在n(t)非常大的时候才能达到,n(t)非常大的时候平滑甚至会失去永久的效应。
趋势项的另外一个作用是稳健性迭代,稳健性权重的目的是减小异常行为的影响,取决于余项的大小,余项的绝对值大的,会给一个小的权重。我们不想让主要的低频因素进入余项,因为我们想给只想给短暂的极值小权重,而不是主要的,缓慢震动的峰值和谷值。鉴于以上目的,我们希望n(t)能小一点。
但是我们不能让n(t)的值太小。选择了n(s)后,因此变化应该进入季节项,我们不希望n(t)太小,以至于一些变异在趋势项中出现。换言之,我们不希望季节项和趋势项竞争数据中的变化。在第五章我们会展示我们需要这样选择n(t)
(因为n(s)>=7,nt的范围在1.5n(p)到2n(p)间)因此,如果我们使n(t)等于满足以上不等式的最小的奇数,以上所有的趋势项的目标都会被满足。在文章中,有3个例子使用了n(t)。在按月的二氧化碳例子中,n(p)=12,n(s)=35,不等式的后面为18.8,所以n(t)=19。对于按天的二氧化碳,n(p)=365,n(s)=3,不等式的后面为572.0,所以n(t)=573。对于事业男性序列,n(p)=12,n(s)=17,不等式右面为19.7,所以n(t)=21
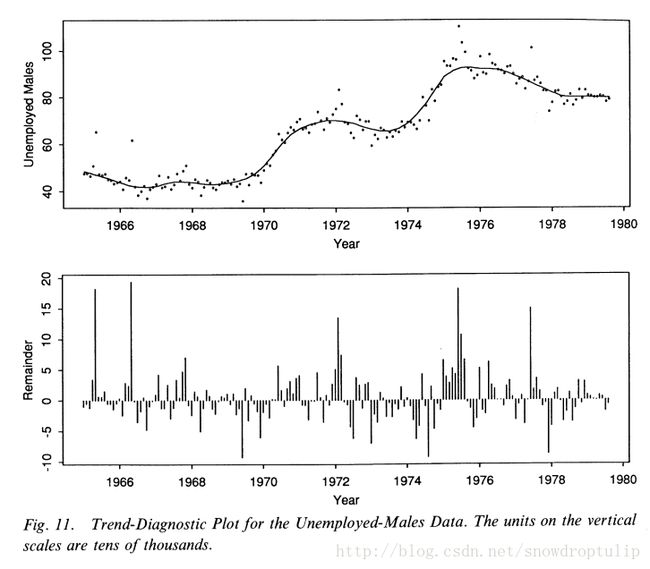
为了得到选择n(t)时趋势项的结果,做一个图11所示的失业男性分解趋势诊断图时有用的。第一幅面板上的点是趋势加上余项,Tv + Rv,Tv是叠加的曲线。下面的面板是余项,Rv;因此底下的图是上面图的残差,因此五月份的异常值在余项图中是非常大的正数。
第四章、计算方法
有一个计算loess平滑的一般原则,就是快速计算。因为是平滑,g(x)无需在所有的x点上精确计算,而是可以精确地计算出足够稠密的点并在其他地方进行插值。计算loess的一般原则的可以有很大的不同,取决于loess的应用环境。
我们用两种方法实现STL,每一种方法都应用了loess快速计算原则,但是两种方法的细节部分却是大不同的。一种方法是在Fortran中实现的,另一种是在S图形和数据分析环境中实现的,在Fortran实现中,有三个计算参数:n(l)(jump), n(t)(jump), n(s)(jump),趋势平滑是在如下点进行完成的:1,1+ n(t)(jump),1+2n(t)(jump),以此类推,直到N点。趋势项在其他点都是通过线性插值来计算的。类似的,在周期子序列平滑过程中,每一个平滑过程都使用了参数为n(s)(jump)loess平滑过程,在低通滤波中使用了参数为n(l)(jump)的loess平滑过程。我们已经发现,使n(t)(jump)为大于等于n(t)/10甚至n(t)/5的最小整数时,效果最好。n(l)(jump), n(s)(jump) 也是一样。在S实现中,每一个loess平滑都是由一个通用loess步骤所完成的,在这个步骤中,选择平滑的点是通过使用k-d树的算法来确定的,并且插值是通过混合函数实现的。
我们对Fortran实现的计算时间进行了分析。Fortran代码是在机器上生成的,是由一个叫Ratfor的Fortran程序员写的。因为更大的速度可以实现,所以不能有缺失值(S实现在上面提到了允许缺失值)。以下STL的参数提供了一个运行时间的合理近似:
常数c1和c2由STL运行的机器决定。对于毫秒级运行的VAX8550,c1= 0.0635,c2= 0.0289。例如,考虑分解第三章的按月的二氧化碳数据,其中N = 348,公式中VAX的运行时间为0.52秒(实际运行时间为0.65秒),对于失业男性的分解,公式中VAX的运行时间是0.73秒(实际运行时间为0.88秒).这个公式,在上面两个例子中,都低估了实际运算时间,但是他的精度满足了我们的目标:粗略的现实,当我们改变参数是,我们可以看到运行时间的变化。例如,我们可以看到,如果都乘以一个引子d,那么运行时间可以被d整除。公式也显示:运行时间与n(i)(n(o)+1)成比例——通过内循环的总次数。