蒙特卡洛模拟Ising模型

蒙特卡洛模拟XY伊辛模型（python）

 

  前言故事

  世界上最早的通用电子计算机之一----ENIAC在发明后即被用于曼哈顿计划，乌拉姆敏锐地意识到在计算机的帮助下，可通过重复数百次模拟过程的方式来对概率变量进行统计估计。冯诺依曼立即认识到这个想法的重要性并给予支持。1947年，乌拉姆提出这种统计方法并应用于计算裂变的连锁反应。由于乌拉姆常说他的叔叔又在蒙特卡洛赌场输钱了，因此他的同事Nicolas Metropolis 戏称该方法为“蒙特卡洛”，不料却流传开去。

算法说明

参考文档：维基百科

1，把握这个算法，首先要体会到随机的意思。这是一个通过随机初始化，然后进行优化的一种算法。

2，直接上算法流程，之后再进行解释。

一，初始化：选择任意一个x0，假设我们的选择服从某种概率分布，比如高斯分布或者平均分布。

二，for i from 0 to N     开始循环迭代

（1）Generate  产生一个候选x 。最简单的方式，随机一个

（2）Calculate  计算接受比 alpha 这里定义的接受比等于 新产生的x在某种分布中的概率/x0在某种分布中的概率。这里的某种分布跟前面的高斯或者平均不是一回事，这里的分布更多的要体现问题的方面。这也是问题在这个算法中唯一的一次介入。

（3）Accepted?

(3_1) 产生一个随机数u,其范围在[0,1]

(3_2) if u<=alpha   那么候选的x就去掉候选状况，正式替代

（3_3）if u>alpha 那么候选的x无效

说明:1,为什么u

我们可以看到，当p(before)=p(after)时，这时，按照我们的常人观点，此时变不变是一半对一半！因为两者的概率一样，所以发生的概率应该一样的。但是这里并不是，如果发生了这种事，直接替换。

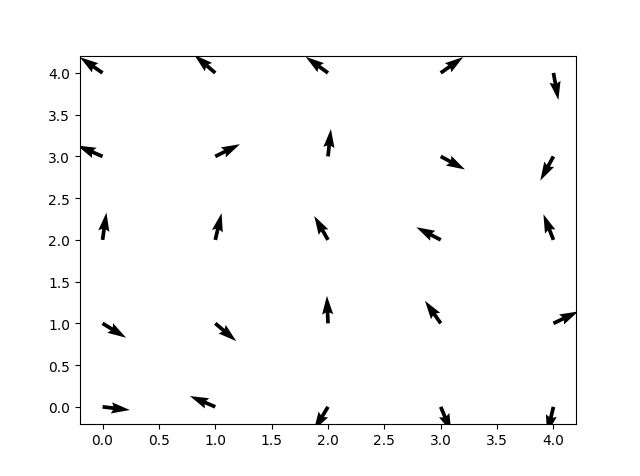
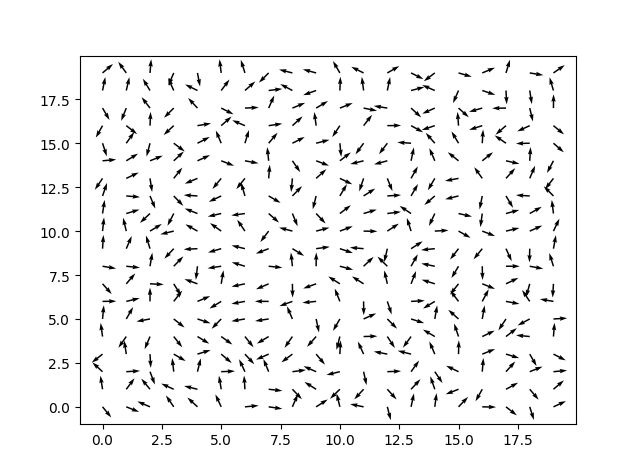
当p(after)

说明2，第（2）步的计算概率是最跟问题有关的。前面的都是随机分布变化，跟问题一点关系没有。请问，问题的概率分布一定存在吗？如果存在，一般怎么构造这种概率表达式？

我也没接触太多。目前，只见到过这个伊辛模型。在热力学统计中，确实有一个物理量对应这种概率分布是多少，称为配分函数。这里是配分函数的统计意义解释。

代码实现

import random
import matplotlib.pyplot as plt
import numpy as np
import copy 
import math
import time
'''这个就是MCMC模拟，用来模拟某个温度下XY Ising模型分布，
几点注意：
注意1，二维伊辛模型，我们用矩阵来模拟。
注意2，旋转的方向，我们用0到2pi表示吧
算法过程：
一，用一个对称的分布，高斯分布初始化矩阵
二，下面是循环
    （1）产生一个候选的自旋方向，为了连续，假设新产生的自旋方向变化最多比原来变化pi/2
    也就是旋转90度
    （2）计算两个概率，这里热统中的配分函数正比于概率，因此我们用配分函数Z的比值
    Z(变化后)/Z(变化前)=exp(-(E后-E前)/kT) ,这里k是玻尔兹曼常数，T是开尔文温度。令
    这个值是alpha
    (3)判断是都接受*********这个规则有进一步讨论*************
         （3_1)产生一个随机数u在【0,1】之间
         （3_2）如果u<=alhpa,接受候选的，改变此时的自旋状态
         (3_3)如果u>alpha，不接受候选的，不改变此时的自旋状态
inputdata: S :matrix 随机分布,假设已经产生
param: T 温度
       delta 最大的变化度数，默认是90度，也可以调整为其他
outputdata:S
'''

def MetropolisHastings(S,T,numsOfItera):
    deltamax=0.5
    
    k = 1  #玻尔兹曼常数 
    for sdw in range(numsOfItera):        
       # k2 = np.random.randint(0,S.shape[0]**2)
        i = np.random.randint(0,S.shape[0])
        j = np.random.randint(0,S.shape[0])
       # print('产生的随机位置是：',i,j)
        #time.sleep(0.1)
        for m in range(1):            
            delta = (2*np.random.random()-1)*deltamax
            newAngle = S[i][j]+delta
           # print(delta)
            energyBefore = getEnergy(i=i,j=j,S=S,angle=None)
            energyLater = getEnergy(i,j,S=S,angle=newAngle)
            alpha = math.exp(-(energyLater-energyBefore)/(k*T))
            #print(alpha)
           # if alpha>=1:
              #  print('大于1的哦')
            if alpha >=1:
                S[i][j]=newAngle
            elif np.random.uniform(0.0,1.0)<=1.0*alpha:
                S[i][j]=newAngle
    return S

#计算i,j位置的能量 = 与周围四个的相互能之和   
def getEnergy(i,j,S,angle=None):
    width = S.shape[0]
    height = S.shape[1]
   # print('矩阵的宽和高是',width,height)
    top_i = i-1 if i>0 else width-1
    bottom_i = i+1 if i<(width-1) else 0
    left_j = j-1 if j>0 else height-1
    right_j = j+1 if j<(height-1) else 0
    enviroment = [[top_i,j],[bottom_i,j],[i,left_j],[i,right_j]]
  #  print(i,j,enviroment)
    #print(enviroment)
    energy = 0
    if angle ==None:
       # print('angle==None')        
        for num_i in range(0,4,1):            
            energy += -np.cos(S[i][j]-S[enviroment[num_i][0]][enviroment[num_i][1]])
    else:
       # print('Angle')
        for num_i in range(0,4,1):
            energy += -np.cos(angle-S[enviroment[num_i][0]][enviroment[num_i][1]])
    return energy

#S=2*np.pi*np.random.rand(30,30)
#计算整个格子的能力，为了求平均内能
def calculateAllEnergy(S):
    energy =0
    for i in range(len(S)):
        for j in range(len(S[0])):
            energy +=getEnergy(i,j,S)
    averageEnergy = energy/(len(S[0])*len(S))
    return averageEnergy/2

#print(S)
#for j in range(1000):
 #   print(j)
   # MetropolisHastings(S,10)
#这个是输入样本的多少，格子的尺寸，温度。中间那个循环，是随机取迭代的过程
def getWeightValue(numsOfSample,sizeOfSample,temperature):
    for i in range(numsOfSample):  #产生个数
        print('+++++++正在计算第%s个样本++++++++++'%i)
        S=2*np.pi*np.random.random((sizeOfSample,sizeOfSample))
        initialEnergy = calculateAllEnergy(S)
        print('系统的初始能量是:',initialEnergy)
        newS = np.array(copy.deepcopy(S))
        for nseeps in range(100):            
            newS = MetropolisHastings(newS,temperature,sizeOfSample**2)
        aveEnergy = calculateAllEnergy(newS)
        plot(newS)
        print('系统的平均能量是:',aveEnergy)
        reshaped = np.reshape(newS,(1,sizeOfSample**2))
        if i ==0:
            s = copy.deepcopy(reshaped)
            continue
        else:
            s = np.row_stack((s,reshaped))
    return s
#运行getweightValue函数，中间已经把结果会成图了
res = getWeightValue(1,40,2)
#print(len(res))
#画成箭头图表示出现
def plot(S):     
    X, Y = np.meshgrid(np.arange(0,S.shape[0]),np.arange(0,S.shape[0]))

    U = np.cos(S)
    V = np.sin(S)

    plt.figure()
    #plt.title('Arrows scale with plot width, not view')
    Q = plt.quiver(X, Y, U, V, units='inches')
#qk = plt.quiverkey(Q, 0.3, 0.3, 1, r'$2 \frac{m}{s}$', labelpos='E',
   #         coordinates='figure')
    plt.show()

 

 

结果展示：

 

 

系统值是：

+++++++正在计算第0个样本++++++++++
系统的初始能量是: 0.006919117595
系统的平均能量是: -0.494289314266
+++++++正在计算第0个样本++++++++++
系统的初始能量是: 0.154688600481
系统的平均能量是: -0.315447987184
+++++++正在计算第0个样本++++++++++
系统的初始能量是: 0.00142378493144
系统的平均能量是: -0.588001265121

跟点击打开链接对比，

我们看到在温度等于2的时候，还是很类似的。

其他温度的结果：