图像处理1--傅里叶变换（Fourier Transform ）

楼下一个男人病得要死，那间壁的一家唱着留声机；对面是弄孩子。楼上有两人狂笑；还有打牌声。河中的船上有女人哭着她死去的母亲。人类的悲欢并不相通，我只觉得他们吵闹 。

OpenCV是一个基于BSD许可（开源）发行的跨平台计算机视觉库，可以运行在Linux、Windows、Android和Mac OS操作系统上。它轻量级而且高效——由一系列 C 函数和少量 C++ 类 构成，同时提供了Python、Ruby、MATLAB等语言的接口，实现了 图像处理和计算机视觉方面的很多通用算法。

OpenCV用C++语言编写，它的主要接口也是C++语言，但是依然保留了大量的C语言 接口。该库也有大量的Python、Java and MATLAB/OCTAVE（版本2.5）的接口。这些语言的API接口函数可以通过在线 文档获得。如今也提供对于C#、Ch、Ruby,GO的支持。

所有新的开发和算法都是用C++接口。一个使用CUDA的GPU接口也于2010年9月开始实现。

图像的空间域滤波：空间域滤波，空间域滤波就是用各种模板直接与图像进行卷积运算，实现对图像的处理，这种方法直接对图像空间操作，操作简单，所以也是空间域滤波。

频域滤波说到底最终可能是和空间域滤波实现相同的功能，比如实现图像的轮廓提取，在空间域滤波中我们使用一个拉普拉斯模板就可以提取，而在频域内，我们使用一个高通滤波模板（因为轮廓在频域内属于高频信号），可以实现轮廓的提取，后面也会把拉普拉斯模板频域化，会发现拉普拉斯其实在频域来讲就是一个高通滤波器。

既然是频域滤波就涉及到把图像首先变到频域内，那么把图像变到频域内的方法就是傅里叶变换。关于傅里叶变换，感觉真是个伟大的发明，尤其是其在信号领域的应用。高通滤波器，又称低截止滤波器、低阻滤波器，允许高于某一截频的频率通过，而大大衰减较低频率的一种滤波器。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。

import cv2 as cv

import numpy as np

from matplotlib import pyplot as plt

 

img = cv.imread('23.png', 0)

f = np.fft.fft2(img)

fshift = np.fft.fftshift(f)

#取绝对值：将复数变化成实数

#取对数的目的为了将数据变化到较小的范围（比如0-255）

s1 = np.log(np.abs(f))

s2 = np.log(np.abs(fshift))

plt.subplot(121),plt.imshow(s1,'gray'),plt.title('original')

plt.subplot(122),plt.imshow(s2,'gray'),plt.title('center')

 

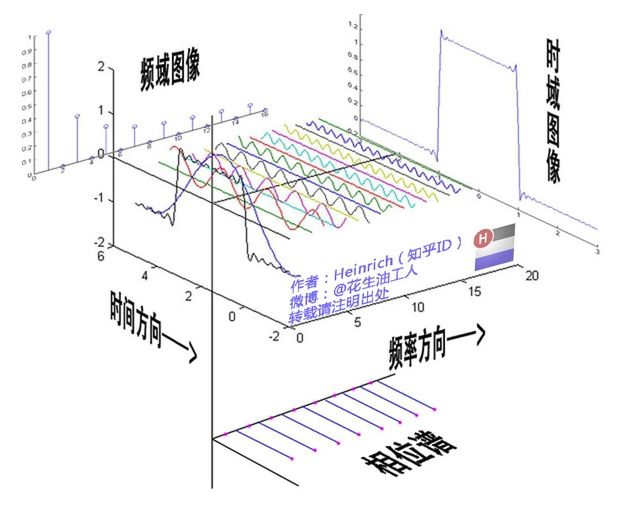
这个图就是把时域图像（大概是方波）变成了一系列的正弦波的线性叠加，其等价关系可以表示为：

f(原始信号)=A1sin(w1x+ϕ1)+A2sin(w2x+ϕ2)+...

那么w1,w2,...可以看成是频率的变化（一般认为就是从1,2,…n定死了），所有的A就是对应频率下的振幅，所有的ϕ就是对应频率下的相位，那么对于任一个信号，如果都认为频率w是从1,2,3…一直增加的话，那么每个信号就只由一组振幅与一组ϕ来决定，他们的不同决定了最终信号的不同。

再来理解下什么是振幅，振幅就是各个频率下的信号的决定程度有多大，如果某个频率的振幅越大，那么它对原始信号的的重要性越大，像上图，当然是w=1的时候振幅最大，说明它对总的信号影响最多（去掉w=1的信号，原始信号讲严重变形）。越往后面，也就是越高频，振幅逐渐减小，那么他们的作用就越小，而他们对于整体信号又有什么影响呢？既然越小，那就是影响小，所以其实去掉，原始信号也基本上不变，他们影响就在于对原始信号的细节上的表现，比如原始信号上的边边角角，偶尔有个小凸起凹槽什么的，这些小细节部分都是靠这些个影响不大的高频信号来表现出来的。深入推广一下，这就很好理解为什么图像的高频信号其实表现出来的就是图像的边缘轮廓、噪声等等这些细节的东西了，而低频信号，表现的却是图像上整块整块灰度大概一样的区域了（这些个区域又称为直流分量区域）。

再来理解下什么是相位，相位表示其实表面对应频率下的正弦分量偏离原点的程度，再借用下上述博客中的一个图，把分量示意图放大了：

上图看到，如果各个频率的分量相位都是0的话，那么每个正弦分量的最大值（在频率轴附近的那个最大值）都会落在频率轴为0上，然而上述图并不是这样。在说简单一点，比如原始信号上有个凹槽，正好是由某一频率的分量叠加出来的，那么如果这个频率的相位变大一点或者变小一点的话，带来的影响就会使得这个凹槽向左或者向右移动一下，也就是说，相位的作用就是精确定位到信号上一点的位置的。 好了，有了上述的概念，再来看看图像的傅里叶变换，上述举得例子是一维信号的傅里叶变换，并且信号是连续的，我们知道图像是二维离散的，连续与离散都可以用傅里叶进行变换，那么二维信号无非就是在x方向与y方向都进行一次一维的傅里叶变换得到，这么看来，可以想象，它的频率构成就是一个网格矩阵了，横轴从w=1到n，纵轴也是这样。所有图像的频率构成都认为是这样的，那么不同的就是一幅图的振幅与相位了（振幅与相位此时同样是一个网格矩阵），也就是说你在opencv或者matlab下对图像进行傅里叶变换后其实是可以得到图像的振幅图与相位图的，而想把图像从频域空间恢复到时域空间，必须要同时有图像的振幅图与相位图才可以，缺少一个就恢复的不完整。

在这里插入一个获取视频的代码

从摄像头捕获视频

OpenCV提供了一个非常简单的接口，用来相机捕捉实时流。
任务：从相机中获取一个视频（由于练习时家里的台式没有摄像头，就直接获取一个本地视频），把它转换成灰度级的视频并显示出来。

要捕获一个视频，你需要创建一个可视的对象cv.VideoCapture()。参数可以是设备索引，也可以是视频文件的名称（这里用视频文件名称）。设备索引只是指定哪个摄像头的号码，如0、1、2。

 1 import cv2 as cv
 2 
 3 cap = cv.VideoCapture('test.mp4')
 4 while cap.isOpened():
 5     # 逐帧捕获
 6     ret, frame = cap.read()
 7     # 对帧进行操作
 8     gray = cv.cvtColor(frame, cv.COLOR_BGR2GRAY)
 9     # 展示结果
10     cv.imshow('frame', gray)
11     if cv.waitKey(1) & 0xFF == ord('q'):
12         break
13 
14 # 一切完成后，释放捕获
15 cap.release()
16 cv.destroyAllWindows()

回到正题，傅立叶空间的变幻代码介绍开始：

1.获取图片振幅信息

 1 import cv2 as cv
 2 import numpy as np
 3 from matplotlib import pyplot as plt
 4 
 5 img = cv.imread('你想要插入的图片', 0#0代表传入的是灰度图像，1代表彩色图像）
 6 f = np.fft.fft2(img)
 7 fshift = np.fft.fftshift(f)
 8 #取绝对值：将复数变化成实数
 9 #取对数的目的为了将数据变化到较小的范围（比如0-255）
10 s1 = np.log(np.abs(f))
11 s2 = np.log(np.abs(fshift))
12 plt.subplot(121),plt.imshow(s1,'gray'),plt.title('original')
13 plt.subplot(122),plt.imshow(s2,'gray'),plt.title('center')

注意的是，这个程序的result其实并没有什么含义，显示出来的可以看成是频域后图像的振幅信息，并没有相位信息，ϕ=atan(实部虚部numpy包中自带一个angle函数可以直接根据复数的实部与虚部求出角度（默认出来的角度是弧度）。像上述程序出来的f与fshift都是复数，就可以直接angle函数一下，比如试试并把对应的相位图像显示出来

 1 import cv2 as cv
 2 import numpy as np
 3 from matplotlib import pyplot as plt
 4 
 5 img = cv.imread('23.png', 0)
 6 
 7 f = np.fft.fft2(img)
 8 fshift = np.fft.fftshift(f)
 9 #取绝对值：将复数变化成实数
10 #取对数的目的为了将数据变化到较小的范围（比如0-255）
11 ph_f = np.angle(f)
12 ph_fshift = np.angle(fshift)
13 
14 plt.subplot(121),plt.imshow(ph_f,'gray'),plt.title('original')
15 plt.subplot(122),plt.imshow(ph_fshift,'gray'),plt.title('center')

View Code

result就是图像上每个像素点对应的相位图，其实是毫无规律的，理解就是偏移的角度。

Ok再来说说程序中为什么要有一个np.fft.fftshift(f)中心化操作，整个图像是在傅里叶变换的一个周期内完成的，将其看成横纵两个方向的一维傅里叶变换，在每个方向上都会有高频信号和低频信号，那么傅里叶变换将低频信号放在了边缘，高频信号放在了中间，然而一副图像，很明显的低频信号多而明显，所以将低频信号采用一种方法移到中间，在时域上就是对f乘以（-1）^(M+N)，换到频域里面就是位置的移到了。

图像变换到频域后就可以进行操作了，目前接触到的频域操作似乎也就是一些滤波操作，如同空域里面的滤波操作一样，不过原理不一样了，后面再说说一些频域滤波方法。好了一旦操作完，得到的数据还是频域数据，那么如何将其变换到时域呢？这里就是傅里叶反变换了，公式表示就如同前面那样。这个频域变换到时域的操作就是逆向傅里叶变换再走一遍（比如先反中心化，在逆变换）。

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 img = cv2.imread('23.png',0) #直接读为灰度图像
 6 f = np.fft.fft2(img)
 7 fshift = np.fft.fftshift(f)
 8 #取绝对值：将复数变化成实数
 9 #取对数的目的为了将数据变化到0-255
10 s1 = np.log(np.abs(fshift))
11 plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')
12 plt.subplot(132),plt.imshow(s1,'gray'),plt.title('center')
13 # 逆变换
14 f1shift = np.fft.ifftshift(fshift)
15 img_back = np.fft.ifft2(f1shift)
16 #出来的是复数，无法显示
17 img_back = np.abs(img_back)
18 plt.subplot(133),plt.imshow(img_back,'gray'),plt.title('img back')

View Code

可以看到恢复的一模一样。

（振幅是复数的实数部，相位是复数的虚数部）我们说，恢复一个频域图像需要图像的振幅以及相位，而一个复数也正好包含这些，振幅就是实部虚部的平方和开方，相位就是atan(实部虚部)

，前面说过。那么现在假设我们只用一副图像的振幅或者相位来将频域内图像恢复到时域会怎么样呢？下面给出只用振幅、只用相位以及两者在联合起来来恢复的程序：

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 img = cv2.imread('23.png',0) #直接读为灰度图像
 6 f = np.fft.fft2(img)
 7 fshift = np.fft.fftshift(f)
 8 #取绝对值：将复数变化成实数
 9 #取对数的目的为了将数据变化到0-255
10 s1 = np.log(np.abs(fshift))
11 plt.subplot(221),plt.imshow(img,'gray'),plt.title('original')
12 plt.xticks([]),plt.yticks([])
13 #---------------------------------------------
14 # 逆变换--取绝对值就是振幅
15 f1shift = np.fft.ifftshift(np.abs(fshift))
16 img_back = np.fft.ifft2(f1shift)
17 #出来的是复数，无法显示
18 img_back = np.abs(img_back)
19 #调整大小范围便于显示
20 img_back = (img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))
21 plt.subplot(222),plt.imshow(img_back,'gray'),plt.title('only Amplitude')
22 plt.xticks([]),plt.yticks([])
23 #---------------------------------------------
24 # 逆变换--取相位
25 f2shift = np.fft.ifftshift(np.angle(fshift))
26 img_back = np.fft.ifft2(f2shift)
27 #出来的是复数，无法显示
28 img_back = np.abs(img_back)
29 #调整大小范围便于显示
30 img_back = (img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))
31 plt.subplot(223),plt.imshow(img_back,'gray'),plt.title('only phase')
32 plt.xticks([]),plt.yticks([])
33 #---------------------------------------------
34 # 逆变换--将两者合成看看
35 s1 = np.abs(fshift) #取振幅
36 s1_angle = np.angle(fshift) #取相位
37 s1_real = s1*np.cos(s1_angle) #取实部
38 s1_imag = s1*np.sin(s1_angle) #取虚部
39 s2 = np.zeros(img.shape,dtype=complex) 
40 s2.real = np.array(s1_real) #重新赋值给s2
41 s2.imag = np.array(s1_imag)
42 
43 f2shift = np.fft.ifftshift(s2) #对新的进行逆变换
44 img_back = np.fft.ifft2(f2shift)
45 #出来的是复数，无法显示
46 img_back = np.abs(img_back)
47 #调整大小范围便于显示
48 img_back = (img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))
49 plt.subplot(224),plt.imshow(img_back,'gray'),plt.title('another way')
50 plt.xticks([]),plt.yticks([])

View Code

 

可以看到，仅仅振幅的恢复图啥也不是，仅仅的相位图还有那么点意思，当然也是啥也不是。最后是把振幅与相位分别作为频域内复数的实部和虚部，得到的恢复图才与原来的一样。

基于此，我们来做一个有趣的实验，假设有两幅图像，将这两幅图像进行傅里叶变换到频域，然后把用一个图像的振幅做为振幅，用另一幅图像的相位作为相位生成一副新的图像，那么，这个图像会怎么样呢？你觉得生成的图像会更像取振幅的那副还是取相位的那副呢？来看看吧：

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 img_flower = cv2.imread('v',0) #直接读为灰度图像
 6 img_man = cv2.imread('v',0) #直接读为灰度图像
 7 plt.subplot(221),plt.imshow(img_flower,'gray'),plt.title('origial1')
 8 plt.xticks([]),plt.yticks([])
 9 plt.subplot(222),plt.imshow(img_man,'gray'),plt.title('origial_2')
10 plt.xticks([]),plt.yticks([])
11 #--------------------------------
12 f1 = np.fft.fft2(img_flower)
13 f1shift = np.fft.fftshift(f1)
14 f1_A = np.abs(f1shift) #取振幅
15 f1_P = np.angle(f1shift) #取相位
16 #--------------------------------
17 f2 = np.fft.fft2(img_man)
18 f2shift = np.fft.fftshift(f2)
19 f2_A = np.abs(f2shift) #取振幅
20 f2_P = np.angle(f2shift) #取相位
21 #---图1的振幅--图2的相位--------------------
22 img_new1_f = np.zeros(img_flower.shape,dtype=complex) 
23 img1_real = f1_A*np.cos(f2_P) #取实部
24 img1_imag = f1_A*np.sin(f2_P) #取虚部
25 img_new1_f.real = np.array(img1_real) 
26 img_new1_f.imag = np.array(img1_imag) 
27 f3shift = np.fft.ifftshift(img_new1_f) #对新的进行逆变换
28 img_new1 = np.fft.ifft2(f3shift)
29 #出来的是复数，无法显示
30 img_new1 = np.abs(img_new1)
31 #调整大小范围便于显示
32 img_new1 = (img_new1-np.amin(img_new1))/(np.amax(img_new1)-np.amin(img_new1))
33 plt.subplot(223),plt.imshow(img_new1,'gray'),plt.title('another way')
34 plt.xticks([]),plt.yticks([])
35 #---图2的振幅--图1的相位--------------------
36 img_new2_f = np.zeros(img_flower.shape,dtype=complex) 
37 img2_real = f2_A*np.cos(f1_P) #取实部
38 img2_imag = f2_A*np.sin(f1_P) #取虚部
39 img_new2_f.real = np.array(img2_real) 
40 img_new2_f.imag = np.array(img2_imag) 
41 f4shift = np.fft.ifftshift(img_new2_f) #对新的进行逆变换
42 img_new2 = np.fft.ifft2(f4shift)
43 #出来的是复数，无法显示
44 img_new2 = np.abs(img_new2)
45 #调整大小范围便于显示
46 img_new2 = (img_new2-np.amin(img_new2))/(np.amax(img_new2)-np.amin(img_new2))
47 plt.subplot(224),plt.imshow(img_new2,'gray'),plt.title('another way')
48 plt.xticks([]),plt.yticks([])

View Code

重点来了：如果两张图片的维度不一样，也就是矩阵的shape不一样时，汇报错ValueError: operands could not be broadcast together with shapes，所以变换的两张图片维度一定要一样，也就是说大小要一样，这个解决了好久，其他也是，两张图片处理时是通过np的方法形成的矩阵，矩阵大小一定要一样才能继续计算，否则是无法处理的。

合成的图像，是不是很有趣，图像3是图1的振幅加图2的相位，图像4是图1的相位加上图2的振幅。很明显的可以看到，新图像占用谁的相位就越像谁，为什么会这样？很简单，可以理解振幅不过描述图像灰度的亮度，占用谁的振幅不过使得结果哪些部分偏亮或者暗而已，而图像是个什么样子是由它的相位决定的。相位描述的是一个方向，方向正确了，那么最终的结果离你的目的就不远了。可想而知，方向对于一件事物是多么的重要，大自然的规律尚且如此，更别说做人做事了，找准并相信一个方向，慢慢的走下去吧，总有一天会看到成果的，哪怕你的振幅不对，走的慢一点，但是最终也能走的像模像样的，不会说到了人生的最后，回头一看，再来感叹哎呀这是什么玩意，那就很悲哀了。

下面开始讲滤波器啦！

我们只说了开头（怎么变换）和结尾（怎么变回去），那么中间我们要做的东西才是傅里叶变换的目的—频域下的各种变化操作。

这里主要介绍频域下的滤波–低通滤波器，高通滤波器，带通带阻滤波器。

我们知道，图像在变换加移动中心后，从中间到外面，频率上依次是从低频到高频的，那么我们如果把中间规定一小部分去掉，是不是相对于把低频信号去掉了呢？这也就是相当于进行了高通滤波。这个滤波模板画出来可能就是这样的：

 

黑色为0，白色为1，把这个模板去和图像进过傅里叶变换的频域矩阵去与（相乘）一下就实现了高通滤波。

高通滤波器代码如下

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 img_man = cv2.imread('lip',0) #直接读为灰度图像
 6 plt.subplot(121),plt.imshow(img_man,'gray'),plt.title('origial')
 7 plt.xticks([]),plt.yticks([])
 8 #--------------------------------
 9 rows,cols = img_man.shape
10 mask = np.ones(img_man.shape,np.uint8)
11 mask[rows//2-30:rows//2+30,cols//2-30:cols//2+30] = 0
12 #--------------------------------
13 f1 = np.fft.fft2(img_man)
14 f1shift = np.fft.fftshift(f1)
15 f1shift = f1shift*mask
16 f2shift = np.fft.ifftshift(f1shift) #对新的进行逆变换
17 img_new = np.fft.ifft2(f2shift)
18 #出来的是复数，无法显示
19 img_new = np.abs(img_new)
20 #调整大小范围便于显示
21 img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
22 plt.subplot(122),plt.imshow(img_new,'gray'),plt.title('Highpass')
23 plt.xticks([]),plt.yticks([])

可以看到，高通滤波器有利于提取图像的轮廓，这里我们从原理上分析一下为什么，图像的轮廓或者边缘或者一些噪声处，灰度变化剧烈，那么在把它们经过傅里叶变换后，就会变成高频信号（我们知道高频时捕捉细节的），所以在把图像低频信号滤掉以后剩下的自然就是轮廓了。也可以这么说，灰度变化剧烈的地方是高频信息，轮廓既是如此。傅立叶空间中亮度代表振幅，振幅越大，亮度越高，该频率下信息越多，而相位则是蕴含着信息。

举手投足山水间，温文尔雅真君子，他与世界相遇 他自与世界相蚀 ，他自不辱使命 使他与众生相聚。

反过来我们来看看空间域滤波中的拉普拉斯模板，现在我们把这个模板进行傅里叶变换到频域看看：

1 import numpy as np
2 import matplotlib.pyplot as plt
4 laplacian = np.array([[0,1,0],[1,-4,1],[0,1,0]])
5 f = np.fft.fft2(laplacian)
6 f1shift = np.fft.fftshift(f)
7 img = np.log(np.abs(f1shift))
8 plt.imshow(img,'gray')

可以看到，这个模板的频域变换下四周特别亮，也就是是个高通滤波器。其它空间域下的模板都可以转到频域下来看看。

下面再来试试低通滤波器什么效果，构造个低通滤波器也很简单，把上述模板中的1变成0,0变成1，其实就是低通了：

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 img_man = cv2.imread('lip',0) #直接读为灰度图像
 5 plt.subplot(121),plt.imshow(img_man,'gray'),plt.title('origial')
 6 plt.xticks([]),plt.yticks([])
 7 #--------------------------------
 8 rows,cols = img_man.shape
 9 mask = np.zeros(img_man.shape,np.uint8)
10 mask[rows//2-20:rows//2+20,cols//2-20:cols//2+20] = 1
11 #--------------------------------
12 f1 = np.fft.fft2(img_man)
13 f1shift = np.fft.fftshift(f1)
14 f1shift = f1shift*mask
15 f2shift = np.fft.ifftshift(f1shift) #对新的进行逆变换
16 img_new = np.fft.ifft2(f2shift)
17 #出来的是复数，无法显示
18 img_new = np.abs(img_new)
19 #调整大小范围便于显示
20 img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
21 plt.subplot(122),plt.imshow(img_new,'gray'),plt.title('Highpass')
22 plt.xticks([]),plt.yticks([])

低通滤波器

可以看到低通滤波后图像除了轮廓模糊了外，基本上没什么变化，图像的大部分信息基本上都保持了。从原理上来看，图像的主要信息都集中在低频上，所以低通滤波器的效果是这样也是可以理解的。上述的高通、低通滤波器的构造有0,1构成的理想滤波器，也是最简单的滤波器，还有一些其他的滤波器，比如说高斯滤波器，butterworth滤波器等等，下面是参考冈萨雷斯书上的图：

 

 还有就是把高通低通都结合一部分到一个模板上形成的带通滤波器，这在一些场合会很有用，还是以理想的带通滤波器实验下：

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 img_man = cv2.imread('lip',0) #直接读为灰度图像
 5 plt.subplot(121),plt.imshow(img_man,'gray'),plt.title('origial')
 6 plt.xticks([]),plt.yticks([])
 7 #--------------------------------
 8 rows,cols = img_man.shape
 9 mask1 = np.ones(img_man.shape,np.uint8)
10 mask1[rows//2-8:rows//2+8,cols//2-8:cols//2+8] = 0
11 mask2 = np.zeros(img_man.shape,np.uint8)
12 mask2[rows//2-80:rows//2+80,cols//2-80:cols//2+80] = 1
13 mask = mask1*mask2
14 #--------------------------------
15 f1 = np.fft.fft2(img_man)
16 f1shift = np.fft.fftshift(f1)
17 f1shift = f1shift*mask
18 f2shift = np.fft.ifftshift(f1shift) #对新的进行逆变换
19 img_new = np.fft.ifft2(f2shift)
20 #出来的是复数，无法显示
21 img_new = np.abs(img_new)
22 #调整大小范围便于显示
23 img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
24 plt.subplot(122),plt.imshow(img_new,'gray')
25 plt.xticks([]),plt.y

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 img_man = cv2.imread('lip',0) #直接读为灰度图像
 5 plt.subplot(121),plt.imshow(img_man,'gray'),plt.title('origial')
 6 plt.xticks([]),plt.yticks([])
 7 #--------------------------------
 8 rows,cols = img_man.shape
 9 mask1 = np.ones(img_man.shape,np.uint8)
10 mask1[rows//2-8:rows//2+8,cols//2-8:cols//2+8] = 0
11 mask2 = np.zeros(img_man.shape,np.uint8)
12 mask2[rows//2-80:rows//2+80,cols//2-80:cols//2+80] = 1
13 mask = mask1*mask2
14 #--------------------------------
15 f1 = np.fft.fft2(img_man)
16 f1shift = np.fft.fftshift(f1)
17 f1shift = f1shift*mask
18 f2shift = np.fft.ifftshift(f1shift) #对新的进行逆变换
19 img_new = np.fft.ifft2(f2shift)
20 #出来的是复数，无法显示
21 img_new = np.abs(img_new)
22 #调整大小范围便于显示
23 img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
24 plt.subplot(122),plt.imshow(img_new,'gray')
25 plt.xticks([]),plt.yticks([])

 

这就是带通的效果，既可以保留一部分低频，也可以保留一部分高频，至于保留多少，怎么保留就视问题的不同而不同了。 

最后声明几点：

1.所有图像处理部分的23.png，lip，v都是我自己测试时用的数据，在自己做图像处理时可以直接替换成相应的文件名（执行的py文件要和图像在同一目录），其他代码视情况改变，如果不是想执行其他功能，可以直接用。

2.结果的图片没有放上，因为用的linux系统，刚刚配置不想截图浪费时间。

3.关于库的问题，ananconda里有numpy，matplotlin.pyplot库，但是cv2库要自己下载，下载方法用pip，一句话，在终端输入如下代码

pip install opencv-python

至于pip的安装：

linux下：

下载文件 wget https://bootstrap.pypa.io/get-pip.py --no-check-certificate

执行安装 python get-pip.py 这就安装好了 

windows下：

参见网址

https://jingyan.baidu.com/article/ff42efa9d630e5c19e220207.html 

 

转载于:https://www.cnblogs.com/klausage/p/10272363.html