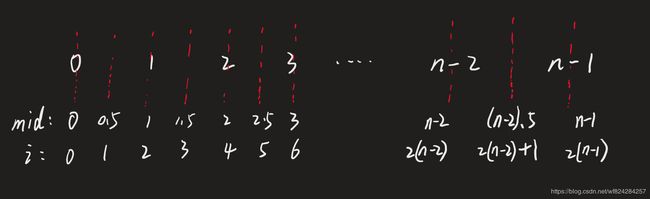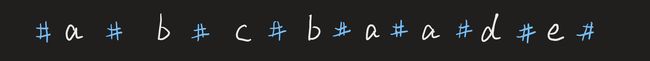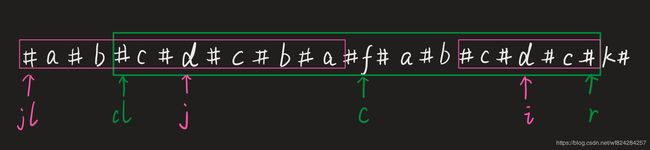LeetCode 5. Longest Palindromic Substring 最长回文子串 C#

前言

本文介绍了 LeetCode 第 5 题 , “Longest Palindromic Substring”, 也就是 “最长回文子串” 的问题.

本文使用 C# 语言完成题目，介绍了 中心扩展法、马拉车算法 等 多种方法供大家参考。

题目

English

LeetCode 5. Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.
Example 2:

Input: “cbbd”
Output: “bb”

中文

LeetCode 5. 最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
示例 2：

输入: “cbbd”
输出: “bb”

解决方案

首先我们会想到使用 暴力法 来解决题目，用3层循环来对每个子串进行检查，最后取最长的子串作为结果，这样时间复杂度为 O(n^3) 。然后可能会考虑到使用动态规划的方式，以空间来换取时间,可以将时间复杂度优化为 O(n^2)，但相应的空间复杂度会增大。

在仔细分析 回文串 的特点后，会想到使用 中心扩展法 ，该方法对于该题目来说不失为一种优秀的解决方法，时间复杂度为 O(n^2)，空间复杂度为 O(1) ; 最后，还介绍了马拉车算法 Manacher ，这是一种非同寻常的算法，充分利用了 回文 的特点， 不可思议的将时间复杂度降为了 O(n) .

下面我们依次来介绍这几种方法。

方法一 : 暴力法

使用 3层循环 来依次对所有子串进行检查，将最长的子串最为最终结果返回。下面代码中，我们检查i到j的子串是否是回文串，如果是 且长度大于当前结果result的长度，就将result更新为i到j的子串。

    public string LongestPalindrome(string s)
    {
        string result = "";
        int n = s.Length;
        for (int i = 0; i < n; i++)
        {
            for (int j = i; j < n; j++)
            {
                // 检查 s[i]到s[j]是否是回文串，如果是，且长度大于result长度，就更新它
                int p = i, q = j;
                bool isPalindromic = true;
                while (p < q)
                {
                    if (s[p++] != s[q--])
                    {
                        isPalindromic = false;
                        break;
                    }
                }
                if (isPalindromic)
                {
                    int len = j - i + 1;
                    if (len > result.Length)
                    {
                        result = s.Substring(i, len);
                    }
                }

            }
        }
        return result;
    }

执行结果

执行结果 超出时间限制。 虽然逻辑上没有问题，可以得到正确结果，但是执行时间过长。

复杂度分析

时间复杂度：O(n^3)

3层循环，所以是 O(n^3) .

空间复杂度：O(1)

仅使用了几个变量来存值，所以为 O(1) .

方法二 : 动态规划

方法一中，存在大量的重复计算工作，例如当 s=“abcba” 时, 对于子串 “bcb” 和 子串 “abcba”, 分别进行了2次完整的计算，来检测该子串是否是回文串。

很明显的是，对于 s=“abcba” , 在已知 "bcb"是回文串的情况下，要判断 "bcb"是否是回文串的话，只需要判断两边的*位置的字符是否相等即可。 我们定义 P(i,j) 表示 s[i,j]是否是回文串，若s[i,j]是回文串，则P(i,j)=true,否则为false. 则有下面的递推公式成立：

P[i,j] =  p(i+1,j-1) && ( s[i]==s[j] ) 

对于上面公式有2个特殊情况，当子串长度为1或2时，上面公式不成立。我们单独分析这两种情况：

若子串长度为1，即 j==i, 则 P[i,j] = P[i,i] = true； 
若子串长为2，即j==i+1, 则 P[i,j] = P[i,i+1] =  ( s[i]==s[i+1] )

在实际执行时，我们先求所有长度为1的子串的P值，再求所有长度为2的子串的P值，之后再求长度3的，以此类推，一直到长度为s.Length的。例如 s=“abcba” ，则P的值 类似下图：

C#代码如下：

    public string LongestPalindrome(string s)
    {
        int n = s.Length;
        bool[,] P = new bool[n, n];
        string result = "";
        //遍历所有的长度
        for (int len = 1; len <= n; len++)
        {
            for (int start = 0; start < n; start++)
            {
                int end = start + len - 1;
                if (end >= n) //下标已经越界，结束本次循环
                    break;
                //长度为 1 和 2 的单独判断下
                P[start, end] = (len == 1 || len == 2 || P[start + 1, end - 1]) && s[start] == s[end];
                if (P[start, end] && len > result.Length)
                {
                    result = s.Substring(start, len);
                }
            }
        }
        return result;
    }

执行结果

执行结果 通过，执行用时 308ms，内存消耗 41.7MB .

复杂度分析

时间复杂度：O(n^2)

两层循环，所以是 O(n^2)

空间复杂度：O(n^2)

P是二维数组，所以是 O(n^2)

方法三 : 中心扩展法

对于回文串，我们可以找到一个中心，从这个中心向两边扩展的话，两边对应的值是相等的。按照这个逻辑，我们只需要一层主循环 i 将 s 遍历一遍即可,并在循环内部 将s[i]视为中心 使用中心扩展法来求出以s[i]为中心的最长的回文串；当i将s遍历完后，即可得到s的最长回文串。

下面我们以 s=“abcbc”, 且 i==2 为例，讨论一下如何进行中心扩展。

1. i==2指向c，我们初始化两个指针p与q都指向这个c
2. p--，q++，p指向了左边b，q指向了右边b
3. 因为s[p]==s[q], 所以再次执行p--,q++,此时p指向了最左边a，q指向了最右边c
4. 因为s[p]!=s[q],所以结束扩展。

此时，我们得到了当i指向中间c时的最长回文子串为"bcb",长度为 q-p-1,开始位置为p+1. 对应图解图下：

当子串长度为奇数时，这个逻辑很容易理解； 当子串长度为偶数时，比如 “abba”，我们需要把中心理解为中轴线，即中轴线在两个b的中间。

将中心理解为中轴线后，中轴线既可以在整数位上，例如"aba"中的b，也可以在两数之间，例如"abba"中的bb之间。若我们用mid表示中轴线，则mid可以等于0、1、2… 也可以等于0.5、1.5、2.5… 对于长度为n的数组，中轴线的选择有 n 个，i 的取值为0到 2(n-1) .

C#代码为：

    public string LongestPalindrome(string s)
    {
        string result = "";
        int n = s.Length;
        int end = 2 * n - 1;
        for (int i = 0; i < end; i ++)
        {
            double mid = i / 2.0;
            int p = (int)(Math.Floor(mid));
            int q = (int)(Math.Ceiling(mid));
            while (p >= 0 && q < n)
            {
                if (s[p] != s[q]) break;
                p--; q++;
            }
            int len = q - p - 1;
            if (len > result.Length)
                result = s.Substring(p + 1, len);
        }
        return result;
    }

执行结果

执行结果 通过，执行用时 112ms，内存消耗 26.2MB .

复杂度分析

时间复杂度：O(n^2)

主循环执行约2n次，内部while最多执行约n/2次（从s最中心向外扩展到s头和s尾），所以复杂度为 O(n^2).

空间复杂度：O(1)

仅使用了几个变量来存值，所以空间复杂度为O(1)

方法四 : 马拉车算法

此方法参考了 leetcode题解中 windliang 贡献的题解、禅道_26ea 的题解、刘毅 的题解。在此感谢 三位，文末给出了他们的题解的链接。

马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法，由一个叫 Manacher 的人在 1975 年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性。

首先我们需要解决s长度可能为奇数或偶数的问题。在每个字符间插入 “#”，经过处理，字符串的长度永远都是奇数了,我们将处理后的字符串记为 。例如s=“abcbaade”，则处理后的字符串 t 如下图所示，长度为 n + (n+1) = 2n+1 .

下面我们来定义三个概念，分别为【回文中心 c】、【回文半径 p】、【回文左右边界 l 和 r】。回文中心 c 的值 表示回文串的中心的 index ，回文半径表示以 c 为中心的最长的回文串的半径长度，回文左右边界 l 和 r 的值 表示 以 c 为中心的最长回文串 的 左右边界的 index。下图1以 "aba"为例，当 c 取 1 时， p=2 , l = 0 , r = 2 . 下图2以 "#a#b#a#"为例，当c取3时 , p=4，l=0 , r=6 。下图3 以 “#a#” 为例，当c取1时， p=2 , l = 0 , r = 2 。 下图4以 “a” 为例，c=l=r=0 , p =1 ; 下图5 再以 "#a#b#a#"为例, 当 c 取为5时，则 l=4 , r=6 , p=2 。即 p、l、r 是依赖于c的，当c取不同的值时，对应的p、l、r 不同，比如例子2和5.

对于处理后的字符串 t , 我们用数组 p 来保存对应的回文半径。例如下图中，p[5]=6,即当 c=5时，p=6 , 对应的字符串为 t[0,10], 即 “#c#b#c#b#c#” . 分析可得，去掉#后的回文串 “cbcbc” 长度为5，正好等于p[5]-1。所以根据 p数组第 i 项 p[i] 的值 , 我们可以得到以 i 为中心的最长回文串 在去掉#后 的 长度为 p[i]-1 ；再进一步，我们不仅可以求得长度，还可以求得它在原字符串中 的 起始index值为 ( i - ( p[i] - 1 ) ) / 2 ,这个可以用下图中的p[5]=6 与 p[7]=4 来验证。

经过上面的分析可以得出：如果是在 p数组的最大值以及对应的index 已知 的情况下 来求解最长的回文串 ，那么题目将会变得非常简单；因为我们可以直接使用2个公式来求出对应的回文串的长度以及起始index，然后从原字符串中取对应的子串即可。这个步骤的时间复杂度为 O(1)。 再分析一下，如果我们分三步走，第一步是求出p数组，第二步是找出p数组的最大值以及index，第三步是使用2个公式求出对应的最长回文子串，则这三步之前的关系是并列的，总复杂度等于三步复杂度之和，且已知第二步复杂度为 O(n), 第三步复杂度为 O(1) , 也就是说，如果我们第一步的复杂度也是O(n)的话，那么算法整体复杂度为 O(n). 所以现在的问题转移为：如何在O(n)的复杂度内求出p数组

如果像方法3一样，遍历 t 数组，并对每个t[i]使用中心扩展法，是可以求的p的，但是时间复杂度就会像方法3一样，变为 O(n^2) .

为了找到思路，可以先来思考这样一个问题。对于 s=“abbbcbbba”, 在已知p的前5位的情况下,是否可以不计算p[5]，而是简单粗暴的 直接让p[5]=p[3]=1 ？ 类似的，直接让p[6]=p[2]=2 ? 直接让p[7]=p[1]=1?

是的，对于这个例子，你可以很坚定的说 “是” 。因为 p[4] = 5,所以s[0,8]是以4为中心的回文串，左右两边具有对称性。这个对称性，是回文串的重要特征之一，但是我们前面3个解法 却没有利用 对称性 来减少计算量。通过这个例子可以察觉到：利用好回文串的对称性，可以省去很多不必要的计算步骤。

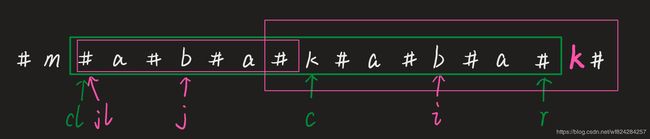
简单来说，我们需要从左到右遍历字符串，并不断的利用已知回文串的对称性，来优化我们的计算过程。下图给了一个例子。

如上图所示，i不断的向右移动，同时用c、l、r 来标记i所遇到过的（以i为中心的）最长的回文串。在i不断的向右移动的过程中，会遇到以下4种情况：

第 1 种情况：下一个要移动的位置在 是 r 或者 r的右边，即 i >= r .

比如在最开始的时候，i=r=0, 当i++时，i>r ,符合这种情况，此时我们需要直接对i进行中心扩展，并更新 c、l、r 的值。

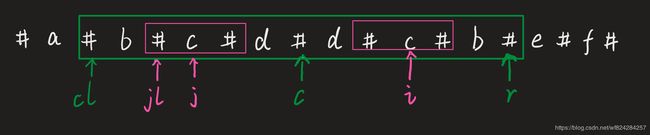
第 2 种情况：下一个要移动的位置在 r 的左边， 且 jl>cl.

cl表示以c为中心的回文串的左边界；

j表示以c为对称中心的 i 的对称点。

jl表示以 j 为中心的回文串的左边界；

这种情况下，p[i]=p[j].

第 3 种情况：下一个要移动的位置在 r 的左边， 且 jl

这种情况下 p[i] = r-i+1

第 4 种情况：下一个要移动的位置在 r 的左边， 且 cl = jl.

这种情况下 p[i]>=p[j] ,所以可以先为p[i]赋值为p[j]，再从r之后往外扩就可以了，扩了之后更新 l、r、c 。

例如：如果最后一位t改为k，则令p[i]=p[j]后，还会从r向右扩展一位。

通过上面分析可知，第2、3种情况，求解p[i]的时间复杂度为 O(1) ， 第1,4种情况求p[i]时，还是需要中心扩展，但是 r 是不断像右扩展的，不会往回退，而且在求解每个p[i]时，r左边的位置是不需要进行判断的，所以在求解p[i]的过程，r的移动是从字符串的起点移动到重点，所以时间复杂度为 O(n).

为了将时间复杂度为 O(n) 的原因表达清楚，我们从头到尾完整的分析一次。首先我们推出了结论若求p数组的时间复杂度为O(n)，则求解最长回文子串算法整体的复杂度为 O(n)，所以可以认为问题转移为 在O(n)复杂度内 求解p数组；为了求解p数组，我们使用i从头到尾遍历数组 这将占用 O(n)的时间复杂度；在求解每个p[i]时，可能遇到上述的4种情况，把求解所有p[i]的步骤加起来，可以总结为 【几个指针从头移动到尾】，假设我们用到了c、r、l 三个指针，则时间复杂度为 O(3n) =O(n) ，这时应该认为算法的总体复杂度为 O(n^2) 吗？因为i占用O(n)，内层循环还占用了 O(n)，所以为 O(n^2)? 仔细思考后，你会发现，虽然内层是个循环，但是内外两个循环并不是【嵌套关系】，而是【并列关系】，对于内层来说，外层的i只是把内层几个变量从头推到尾而已，并没有重复计算。认识到两者是并列关系后，我们得出算法整体的复杂度、也就是内外复杂度之和为 O(n+n)=O(2n)=O(n), 即还是线性复杂度。为何 O(2n) =O(n) ? 是因为算法的时间复杂度一般只需要取最高次数的项就好了，系数常数等可以去掉。

根据上面的分析，我们C#代码如下：

    public string PreProcess(string s)
    {
        string t = "";
        int n = s.Length;
        if (n == 0) return "";
        for (int i = 0; i < n; i++)
        {
            t += "#" + s[i];
        }
        t += "#";
        return t;
    }

    public string LongestPalindrome(string s)
    {
        string t = PreProcess(s);
        int n = t.Length;
        int[] p = new int[n];
        int c = 0, r = 0;
        //计算P
        for (int i = 1; i < n - 1; i++)
        {
            int j = 2 * c - i;
            //情况2和3可以总结为 p[i]= min(r - i + 1, p[j]) ,情况1为 p[i]=1;
            p[i] = r > i ? Math.Min(r - i + 1, p[j]) : 1;
            //对于情况4和1，直接扩展即可；
            //对于情况2和3，也可以直接扩展；虽然一定扩展不了，但是这样的计算过程比“判断是情况2或3”的计算量还要小，仔细品味
            while (i + p[i] < n && i - p[i] >= 0)
            {
                if (t[i - p[i]] == t[i + p[i]]) p[i]++;
                else break;
            }
            if (i + p[i] > r)
            {
           //找到了更长的回文串，更新c和r
                c = i;
                r = i + p[i] - 1;
            }
        }
        // 找出 P 的最大值
        int maxLen = 0;
        int centerIndex = 0;
        for (int i = 1; i < n - 1; i++)
        {
            int len = p[i] - 1;
            if (len > maxLen)
            {
                maxLen = len;
                centerIndex = i;
            }
        }
        int start = (centerIndex - maxLen) / 2;
        return s.Substring(start, maxLen);
    }

根据 windliang 提供的题解思路，可将PreProcess 方法做一些优化，来简化对字符串首尾的判断。优化后的代码如下：

    public string PreProcess(string s)
    {
        string t = "^";
        int n = s.Length;
        if (n == 0) return "^$";
        for (int i = 0; i < n; i++)
        {
            t += "#" + s[i];
        }
        t += "#$";
        return t;
    }

    // 方法四：马拉车算法 108ms,26.4M
    public string LongestPalindrome(string s)
    {
        string t = PreProcess(s);
        int n = t.Length;
        int[] p = new int[n];
        int c = 0, r = 0;
        //计算P
        for (int i = 1; i < n - 1; i++)
        {
            int j = 2 * c - i;
            //情况2和3可以总结为 p[i]= min(r - i + 1, p[j]) ,情况1为 p[i]=1;
            p[i] = r > i ? Math.Min(r - i + 1, p[j]) : 1;
            //对于情况4和1，直接扩展即可；
            //对于情况2和3，也可以直接扩展；虽然一定扩展不了，但是这样的计算过程比“判断是情况2或3”的计算量还要小，仔细品味
            while (t[i - p[i]] == t[i + p[i]])
            {
                p[i]++;
            }
            if (i + p[i] > r)
            {
                //找到了更长的回文串，更新c和r
                c = i;
                r = i + p[i] - 1;
            }
        }
        // 找出 P 的最大值
        int maxLen = 0;
        int centerIndex = 0;
        for (int i = 1; i < n - 1; i++)
        {
            int len = p[i] - 1;
            if (len > maxLen)
            {
                maxLen = len;
                centerIndex = i;
            }
        }
        int start = (centerIndex - maxLen) / 2;
        return s.Substring(start, maxLen);
    }

执行结果

执行结果 通过，执行用时 108ms，内存消耗 26.4MB .

复杂度分析

时间复杂度：O(n)

求解过程见上文。

空间复杂度：O(n)

因为p数组空间复杂度为 O(n).

参考资料汇总

题目：

https://leetcode-cn.com/problems/longest-palindromic-substring/

官方题解：

https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode/

windliang 题解：

https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-bao-gu/

刘毅 题解：

https://segmentfault.com/a/1190000008484167?utm_source=tag-newest

禅道_26ea 题解：

https://www.jianshu.com/p/116aa58b7d81