综合评价与决策方法（待补全）

综合评价与决策方法

理想解法

定义及有关概念

多属性决策问题的理想解法，亦称TOPSIS法，即各指标的最优解和最劣解。

多属性决策方案集$D$={$d_1,d_2,...,d_m$}

衡量方案优劣的属性变量为$x_1,x_2,...,x_n$

属性值类型包括效益型，成本型，区间型等。效益型属性值越大越好，成本型属性值越小越好，区间型属性值在某个区间最佳。

方案集里的每一方案$d_i$的n个属性值构成向量为$[a_{i1},a_{i2},...,a_{in}]$,是n维空间的一个点，可以唯一表征方案$d_i$

正理想解$C^{\ast }$是方案集里不存在的虚拟最佳方案，它的每个属性值都是决策矩阵中该属性的最优值

负理想解$C^0$是方案集里不存在的虚拟最差方案，它的每个属性值都是决策矩阵中该属性的最差值

方案的优先序，在n维空间中，将方案$D$中的备选方案$di$与正理想解和负理想解的距离进行比较，既靠近正理想解又远离负理想解的方案就是最优方案

TOPSIS法的算法步骤

1. 用向量规划化的方法求规范决策矩阵。设多属性决策问题的决策矩阵$A=(a_{ij}{)}_{m\times n}$,规范化决策矩阵$B=(b_{ij}{)}_{m\times n},$其中
   $$b_{ij}=a_{ij}/\sqrt{\sum _{i=1}^m{a}_{ij}^2},i=1,2,...,m;j=1,2,...,n。$$

2. 构造加权规范阵$C=(c_{ij}{)}_m\times n。$设由决策人给定各属性的权重向量为$\omega =[{\omega }_1,{\omega }_2,...,{\omega }_n{]}^T,$则
   $$c_{ij}={\omega }_j\cdot b_{ij},i=1,2,...,m;j=1,2,...,n。$$

3. 确定正理想解和负理想解。设正理想解$C^{\ast }$的第j个属性值为$c_j^{\ast }$，负理想解$$C^0$$的第j个属性值为$c_j^0$，
   $$\begin{gathered} c_j^{\ast }=\{\begin{array}{ll}max& c_{ij},j为效益型属性\\ min& c_{ij},j为成本型属性\end{array},j=1,2,...,n, \\ {c}_j^0=\{\begin{array}{ll}min& c_{ij},j为效益型属性\\ max& c_{ij},j为成本型属性\end{array},j=1,2,...,n。 \end{gathered}$$

4. 计算各方案到正负理想解的距离。
   $$\begin{gathered} s_i^{\ast }=\sqrt{\sum _{j=1}^n(c_{ij}-c_j^{\ast }{)}^2},i=1,2,...,m; \\ {s}_i^0=\sqrt{\sum _{j=1}^n(c_{ij}-c_j^0{)}^2},i=1,2,...,m。 \end{gathered}$$

5. 计算个方案的排序指标值(即综合评价指数)，即
   $$f_i^{\ast }=\frac{s_i^0}{s_i^0+s_i^{\ast }},i=1,2,...,m。$$

6. 按$f_i^{\ast }$由大到小排列方案的优劣次序

实例及解题步骤

一.属性值的规范化

规范化的目标：①使不同类型的属性值可以直接从数值大小判断优劣，方案越优，属性值越大。②非量纲化，即排除量纲的选用对决策或评估结果的影响③归一化，即将表中的数值变换到[0,1]区间上。

1. 线性变换。设$a_j^{max}$是决策矩阵第j列最大值，$a_j^{min}$是决策矩阵第j列最小值。则

$$b_{ij}=\{\begin{array}{l}{a}_{ij}/a_j^{max},x_i为效益型属性,\\ 1-a_{ij}/a_j^{max},x_i为效益型属性。\end{array}$$

2. 标准0-1变换。
   $$b_{ij}=\{\begin{array}{l}\frac{a_{ij}-a_j^{min}}{a_j^{max}-a_j^{min}},x_i为效益型属性,\\ \frac{a_j^{max}-a_{ij}}{a_j^{max}-a_j^{min}},x_i为效益型属性。\end{array}$$

3. 区间型属性的变换。设定最优属性区间为[$a_j^0,a_j^{\ast }$],$a_j^{{}^{\prime }}$为违法容忍下限，$a_j^{{}^{\prime \prime }}$为无法容忍上限，则
   $$b_{ij}=\{\begin{array}{l}1-\frac{a_j^0-a_{ij}}{a_j^0-a_j^{{}^{\prime }}},a_j^{{}^{\prime }}⩽a_{ij}<a_j^0\\ 1,a_j^0⩽a_{ij}⩽a_j^{\ast }\\ 1-\frac{a_{ij}-a_j^{\ast }}{a_j^{{}^{\prime \prime }}-a_j^{\ast }},a_j^{\ast }<a_{ij}⩽a_j^{{}^{\prime \prime }}\\ 0,其他\end{array}$$

4. 向量规范化。无论成本型还是效益型属性，向量规范化均用下式进行变换：
   $$b_{ij}=a_{ij}/\sqrt{\sum _{i=1}^m{a}_{ij}^2},i=1,2,...,m;j=1,2,...,n。$$
   变换后属性值的大小无法辨别属性值的优劣，常用于计算各方案与某种虚拟方案的欧几里得距离

5. 标准化处理。消除变量的量纲效应
   $$b_{ij}=\frac{a_{ij}-{\overline{a}}_j}{s_j},i=1,2,...,m,j=1,2,...,n,$$
   式中:${\overline{a}}_j=\frac{1}{m}{\sum }_{i=1}^m{a}_{ij},s_j=\sqrt{\frac{1}{m-1}{\sum }_{i=1}^m(a_{ij}-{\overline{a}}_j{)}^2},j=1,2,...,n。$

二.设权重向量，求加权的向量规范化矩阵
$$c_{ij}={\omega }_j\cdot b_{ij},i=1,2,...,m;j=1,2,...,n。$$
三.求正负理想解

四.求各方案到正负理想解的距离

五.计算排序指标值

MATLAB伪代码

clc,clear;
输入决策矩阵a;
[m,n]=size(a);
定义函数进行变换;
若有区间型属性，则定义qujian=[aj_0,aj_star],lb,ub;
对区间型属性进行变换;
for j=1:n
	b(:,j)=a(:,j)/norm(a(:,j));	   %向量规划化求规范化决策矩阵
end
输入权重w;
c=b.*repmat(w,m,1);	   %求加权矩阵
Cstar=max(c);	%求正理想解，max可返回每列最大值
将成本型属性对应的Cstar元素用c对应列的最小值代替
C0=min(c);    %求负理想解
将成本型属性对应的C0元素用c对应列的最大值代替
for i=1:m
	Sstar(i)=norm(c(i,:)-Cstar);    %求每一方案到正理想解的距离
	s0(i)=norm(c(i,:)-c0);    %求每一方案到负理想解的距离
end
Sstar,s0	%显示到正理想解和负理想解的距离
f=s0./(Sstar+s0);
[sf,ind]=sort(f,'descend');%sf为从大到小排序后的f,ind为排序后的序号即f(ind(1))=sf(1)

数据包络分析(DEA)

定义及有关概念

它是根据多项投入指标和多项产出指标，利用线性规划的方法，对具有可比性的同类型单位(也可称决策单元，DMU)进行相对有效性评价的一种数量分析方法。用于解决相对有效评价问题。

设有$n$个DMU,每个DMU都有$m$种投入和$s$种产出，设$x_{ij}(i=1,...,m;j=1,...,n)$表示第$j$个DMU的第$i$种投入量，$y_{rj}(r=1,...,s;j=1,\dots ,n)$表示第$j$个DMU的第$r$种产出量，

决策单元$j$的投入向量$X_j=(x_{1j},x_{2j},...,x_{mj}{)}^T$

决策单元$j$的产出向量$Y_j=(y_{1j},y_{2j},...,y_{sj}{)}^T$

决策单元$j$的投入权值向量$\nu =(v_1,v_2,...,v_m{)}^T$

决策单元$j$的产出权值向量$u=(u_1,u_2,...,u_s{)}^T$

决策单元$j$的效率评价指数$h_j=\frac{u^T{Y}_j}{{\nu }^T{X}_j},j=1,2,...,n。$

$C^{2}R$模型

评价决策单元$j_0$效率的数学模型为
$$\begin{gathered} max\frac{u^T{Y}_{j0}}{{\nu }^T{X}_{j0}}, \\ s.t.\{\begin{array}{l}\frac{u^T{Y}_{j0}}{{\nu }^T{X}_{j0}}⩽1,j=1,2,...,n,\\ u⩾0,\nu ⩾0,u\ne 0,\nu \ne 0。\end{array} \end{gathered}$$
通过Charnes-Cooper变换:$\omega =t\nu ,\mu =tu,t=\frac{1}{{\nu }^T{X}_{j0}},$可以将上述模型转化为等价的线性规划问题
$$\begin{gathered} max{V}_{j0}={\mu }^T{Y}_{j0}, \\ s.t.\{\begin{array}{l}{\omega }^T{X}_j-{\mu }^T{Y}_j⩾0,j=1,2,...,n,\\ {\omega }^T{X}_{j0}=1,\\ \omega ⩾0,\mu ⩾0。\end{array}----(16) \end{gathered}$$
写出上述模型的对偶形式:
$$\begin{gathered} min\theta , \\ s.t.\{\begin{array}{l}{\sum }_{j=1}^n{\lambda }_j{X}_j⩽\theta X_{j0},\\ {\sum }_{j=1}^n{\lambda }_j{Y}_j⩾Y_{j0},\\ {\lambda }_j⩾0,j=1,2,...,n。\end{array} \end{gathered}$$
对于$C^{2}R$模型(16)，有如下定义:

若线性规划问题(16)的最优化目标值$V_{j0}=1$，则称决策单元$j_0$是弱DEA有效的。

若线性规划问题(16)存在最优解${\omega }^{\ast }>0,{\mu }^{\ast }>0,$并且其最优目标值$V_{j0}=1$，则称决策单元$j_0$是DEA有效的。

注意：在此模型下w$=x=[{\omega }^T,{\mu }^T]$，即权重w为线性规划的向量，$f=[zeros(1,m),-Y(:,i{)}^{\prime }]$(实测出现了f不论是行向量还是列向量都返回同样的w的情况)。

$C^{2}R$的MATLAB伪代码

输入投入向量X；
输入产出向量Y;
n=size(X',1);
m=size(X,1);
s=size(Y,1);
A=[-X' Y'];
b=zeros(n,1);
LB=zeros(m+s,1);
UB=[];
for i=1:n
	f=[zeros(1,m),-Y(:,i)'];
	Aeq=[X(:,i)' zeros(1,s)];
	beq=1;
	w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);
	E(1,i)=Y(:,i)'*w(m+1:m+s,i);%求DMU的相对效率值
end

灰色关联分析法

定义及有关概念

灰色关联分析法，是根据因素之间发展趋势的相似或相异程度，作为衡量因素间关联程度的一种方法。

关联度是对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度。在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。

==比较对象(评价对象)==可理解为DEA中的决策单元。

==参考数列(评价标准)==类似于TOPSIS中的理想解，指标标准化后参考数列就是由每个指标的最大值构成的向量。

具体步骤

1. 确定参考数列和比较数列，设评价对象有$m$个，指标有$n$个。比较数列是输入矩阵的每一列，记为$x_i$。参考数列记为$x_0$。
   $$x_i=\{x_i(k)|k=1,2,...,n\},i=1,2,...,m。x_0=\{x_0(k)|k=1,2,...,n\}$$

2. 对输入矩阵进行规范化处理。过程参考TOPSIS。

3. 确定各指标值对应的权重。可用层次分析法等确定，记为w$=[w_1,w_2,...,w_n]$。

4. 计算灰色关联系数:
   $${\xi }_i(k)=\frac{minmin|x_0(t)-x_s(t)|+\rho maxmax|x_0(t)-x_s(t)|}{|x_0(k)-x_i(k)|+\rho maxmax|x_0(t)-x_s(t)|}$$
   为比较数列$x_i$对参考数列$x_0$在第$k$个指标上的关联系上，其中$\rho \in [0,1]$为分辨系数。称$minmin|x_0(t)-x_s(t)|,maxmax|x_0(t)-x_s(t)|$分别为两级最小差及两级最大差。

5. 计算灰色加权关联度:
   $$r_i=\sum _{k=1}^n{w}_i{\xi }_i(k),$$
   式中$r_i$为第$i$个评价对象对理想对象的灰色加权关联度。

6. 评价分析。根据灰色加权关联度的大小，对各评价对象进行排序。

MATLAB伪代码

输入参考数据矩阵;
for i=...%效益型指标标准化,此处采用标准0-1变换
	a(i,:)=(a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i=...%成本型指标标准化,此处采用标准0-1变换
	a(i,:)=(max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end
[m,n]=size(a);
cankao=max(a')';%求参考序列的值
t=repmat(cankao,[1,n])-a;%求参考序列与每一序列的差
mmin=min(min(t));%两级最小差
mmax=max(max(t));%两级最大差
给定分辨系数rho;
xishu=(mmin+rho*mmax)./(t+rho*mmax);
guanliandu=mean(xishu);%取等权重，计算关联度,mean函数求每一列的平均值
[gsort,ind]=sort(guanliandu,'descend');%按关联度从大到小排序

主成分分析法(Principal Component Analysis，PCA)

定义及有关概念

PCA是一种常用的数据分析方法，通过线性变换将原始数据变换为一组各维度线性无关的表示，常用于数据降为。它用几个不相关的综合变量来较全面的反应整个数据集，这些综合变量称为主成分，各主成分间线性无关。

基本步骤

假设样本数量为$n$，指标数量为$m$。

1.数据标准化。将各指标$a_{ij}$转换成标准化指标$a_{ij}$，
$${\tilde{a}}_{ij}=\frac{a_{ij}-u_j}{s_j},i=1,2,...,n,j=1,2,...,m$$
式中：$u_j，s_j$为第$j$个指标的样本均值个样本标准差。称${\tilde{a}}_{ij}$为对应的标准化指标变量。

2.计算相关系数矩阵$R=(r_{ij}{)}_{5\times 5}$，或者计算协方差矩阵，以计算系数阵为例。
$$r_{ij}=\frac{{\sum }_{k=1}^n{\tilde{a}}_{ki}\cdot \widetilde{a_{kj}}}{n-1},i,j=1,2,...,m$$
其中$r_{ij}=r_{ji},r_{ii}=1$

3.计算特征值和特征向量，用特征值进行排序，用对应的特征向量生成$m$个新的指标向量，假设根据特征值排好序的向量为$u_j=[u_{1j},u_{2j},...,u_{nj}],j=1,2,...,m$。
$$\begin{gathered} y_1=u_{11}{\tilde{x}}_1+u_{21}{\tilde{x}}_2+...+u_{m1}{\tilde{x}}_m \\ {y}_2=u_{12}{\tilde{x}}_1+u_{22}{\tilde{x}}_2+...+u_{m2}{\tilde{x}}_m \\ ⋮ \\ {y}_m=u_{1m}{\tilde{x}}_1+u_{2m}{\tilde{x}}_2+...+u_{mm}{\tilde{x}}_m \end{gathered}$$
4.选取$p(p\le m)$个主成分，计算综合评价值

• 计算某一特征值(主成分)和前$p$个特征值(主成分)的信息贡献率，记为$b,{\alpha }_p$。

$$\begin{gathered} b_j=\frac{{\lambda }_j}{{\sum }_{k=1}^m{\lambda }_k},j=1,2,...,m \\ {\alpha }_p=\frac{{\sum }_{k=1}^p{\lambda }_k}{{\sum }_{k=1}^m{\lambda }_k} \end{gathered}$$

• 计算综合得分

$$Z=\sum _{i=1}^p{b}_j{y}_j$$

MATLAB伪代码

clc,clear;
a=load('data.txt');
a=zscore(a);%数据标准化
r=corrcoef(a);
[x,y,b]=pcacov(r);%x是特征向量所构成的矩阵，y是特征值，b为各个主成分的贡献率
f=repmat(sign(sum(x)),size(x,1),1); %构造与x同维数的元素为±1的矩阵,sign函数返回-1或+1取决于自变量是否大于0
x=f.*x;
num=p;%num为选取的主成分的个数
score=a*x(:,[1:num])/100;  %计算各个主成分的得分
z=score*b(1:num); %计算综合得分
[sz,ind]=sort(z,'descend');  %把得分按照从高到低的次序排列
sz=sz', ind=ind'

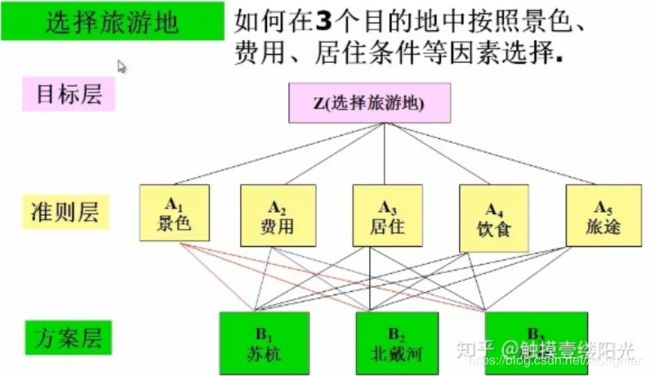
层次分析法(Analytic Hierarchy Process)

定义及有关概念

这种方法的特点就是在对复杂决策问题的本质、影响因素及其内在关系等进行深入研究的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。是对难以完全定量的复杂系统做出决策的模型和方法。

若矩阵$A=(a_{ij}{)}_{n\times n}$满足$a_{ij}>0且a_{ji}=\frac{1}{a_{ij}}(i,j=1,2,...,n)$称之为正互反矩阵。

满足$a_{ij}{a}_{jk}=a_{ik},\forall i,j,k=1,2,...,n$的正互反矩阵称为一致矩阵。

基本步骤

1.建立层次结构模型

2.构造成对比较矩阵

比较矩阵的元素$a_{ij}$表示的是第$i$个因素相对于第$j$个因素的比较结果，这个值使用的是Santy的1-9标度方法给出

例如

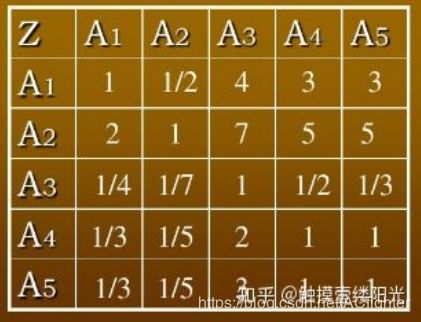
这个矩阵由建模者主观给出，通过求比较矩阵的最大特征值所对应的特征向量，就可以获得不同因素的权重，归一化一下(每个权重除以权重和作为自己的值，最终总和为1)就更便于使用了。

3.层次单排序和一致性检验

获得比较矩阵后可求其最大特征根${\lambda }_{max}$的特征向量，经归一化后记为$W$，这一过程称为层次单排序。能否确认层次单排序，则需要进行一致性检验。定义一致性指标为：$CI=\frac{\lambda -n}{n-1}$，为衡量$CI$的大小，引入随机一致性指标$RI=\frac{C{I}_1+C{I}_2+...+C{I}_n}{n}$，但是似乎没有算的必要其取值可直接参照表格：

矩阵阶数	1	2	3	4	5	6	7	8	9	10
$RI$	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

引入检验系数$CR=\frac{CI}{RI}$，一般如果$CR<0.1$则认为通过一致性检验。

4.层次总排序及决策(方案层各方案对应准则进行互相比较)

注意，若给定数据中各个方案的准则层有可以量化的属性值，则此步骤可以不执行，运用单排序的权值进行TOPSIS就可以进行决策。

次级标题可能过与抽象，举个例子。现有三个候选人y1,y2,y3，要从中选一个总体上最适合的候选人，给定五个条件品德(x1)，才能(x2)，资历(x3)，年龄(x4)，群众关系(x5)。对此，对三个候选人y = y1,y2,y3分别比较。得到5个3$\times$3的矩阵$B_1,…,B_5$。

分别对$B_1,...,B_5$进行层次单排序和一致性检验可以获得5个3维向量$w_1,...,w_5$分别是三个候选人的某一项指标得分。总得分$s(y_i)={\sum }_{j=1}^{5}W(j)w_j(i)$，最后只要进行排序就可以得到最佳方案，至此AHP结束。

MATLAB伪代码

clc,clear;
fid=fopen('shuju.txt','r');
n1=准则个数;n2=方案个数;
a=[];b=[];%初始化准则层比较矩阵a和方案层比较矩阵b
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%以下代码一定要一遍跑，或者写到m函数运行保存数据，读取
for i=1:n1
	tmp=str2num(fgetl(fid));
	a=[a;tmp];
end
for j=1:n2*n1
    tmp=str2num(fgetl(fid));
    b=[b;tmp];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);%求a的特征向量
lamda=max(diag(y));%求出最大特征值
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));%准则层权重
cr0=(lamda-n1)/(n1-1)/ri(n1)%小于0.1则采纳
for i=1:n1
    t=b((i-1)*3+1:3*i,:);%中间矩阵即Bi
    [x,y]=eig(t);
    lamda=max(diag(y));
    num=find(diag(y)==lamda);
    w1(:,i)=x(:,num)/sum(x(:,num));%方案层权重
    cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1%输出一致性比率
ts=w1*w0%输出各方案的分数
cr=cr1*w0%输出总体一致性比率