最小生成树——贪心算法

1.生成树和最小生成树

1.1 问题的定义

一个连通图 的生成树是一个极小连通子图，它含有图中全部的顶点，但是只有足有构成一棵树的n-1条边。它有如下性质：

• 一棵有$n$个顶点的生成树有且只有$n-1$条边；
• 如果一个图有$n$个顶点和小于$n-1$条边，则是非连通图；如果它多于$n-1$条边，则一定有环；
• 但是有$n-1$条边的$n$个顶点的图不一定是生成树。（它只是必要条件）

一棵生成树的代价就是树上各边的代价之和。
最小生成树就是构造连通网 的最小代价生成树（Minimum Cost Spanning Tree)（简称为最小生成树）的问题。

1.2 MST性质

构造最小生成树有多种算法，其中多数算法利用了最小生成树的一种简称为MST的性质：
假设 N=（V，{E}）是一个连通网，U是顶点集V的一个非空子集。
若（$u,v$）是一条具有最小权值（代价）的边，其中$u\in U，v\in V-U$,则必存在一棵包含边($u,v$)的最小生成树。
证明：（反证法）
假设网N的任何一棵生成树都不包含（$u,v$）。设T是连通图上的一棵最小生成树，当将边（$u,v$）加入到T中时，由生成树的性质，T中必存在一条包含（$u,v$）的回路。
另一方面，由于T是生成树（极小连通图），则T上必存在另一条边（$u^{{}^{\prime }},v^{{}^{\prime }}$），其中$u^{{}^{\prime }}\in U，v^{{}^{\prime }}\in V-U$,且$u$和$u^{{}^{\prime }}$之间，$v$和$v^{{}^{\prime }}$之间均有路径相通。删去边$(u^{{}^{\prime }},v^{{}^{\prime }})$，便可以消除上诉回路，同时得到另一棵更小代价的生成树$T^{{}^{\prime }}$，这与假设矛盾。

简单点来说，将这条代价最小的边加入当前的生成树T会有环，再在环上找另一条代价更大的边去除然后就能得到代价更小的生成树$T^{{}^{\prime }}$，所以原代价最小的边一定在最后的生成树中.

2.普里姆算法（Prim）

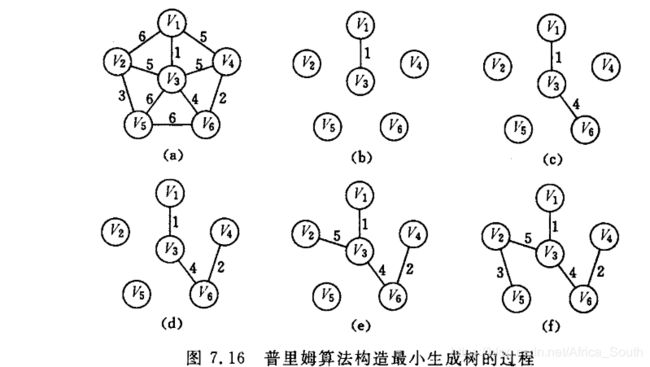
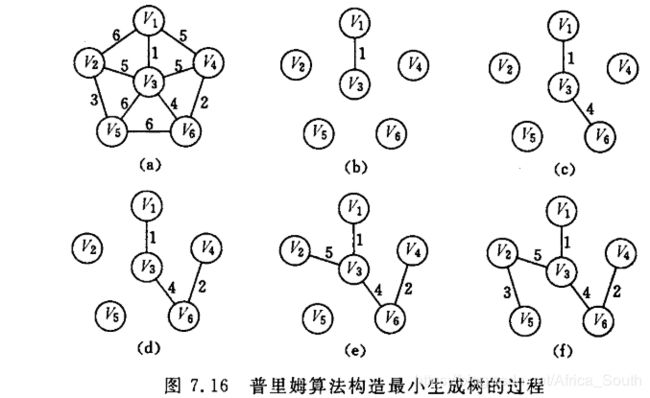
2.1 算法流程

假设N=（V，{E}）是连通网，TE是N上最小生成树中边的集合。

• 假设 $U$ 是最小生成树中的顶点集合， $TE$ 是最小生成树中的边的集合
• 算法从 $U=\{u_0\}（u_0\in V$），$TE=\{\}$ 开始，重复执行下述操作：
• 在所有 $u\in U，v\in V-U$的边 $(u,v)\in E$ 中找一条代价最小的边 $(u_0,v_0)$ 并入集合TE，同时$v_0$并入U，直到 $U=V$ 为止。此时TE中必有 $n-1$ 条边，则T=（V,{TE}）为N的最小生成树。
• 注意，每次在选择最小边 $(u_0,v_0)$ 时候，需要判断点 $v_0$ 是否已经并入集合 $U$, 即判断该边的加入是否会产生环路。

简单来说，就是从任意点u0出发，然后不断在所有U中顶点的邻接边中找一个加入不会构成环的顶点并入U直到U=V

举个栗子

上述过程从U=V1开始。

2.2 算法正确性证明

Prim算法的思想是贪心算法，其正确性可以通过贪心准则的最优性来证明，常用的有贪心交换和数学归纳法。
数学归纳法：
1.选择第一条边的时，由MST性质，一定是权值最小的边；
2.假设我们选取的前s条边是最小生成树的一部分，这些边连接结点记作$n_0,n_1,...,n_s$。
接下来，选择下一条边的时候，我们将选择与这$s+1$个点相连的所有边中最小边，我们可以用反证法证明，这条边一定在最后的生成树中。
假设这条边的一端是$n_i,i\in [0,s]$，另一端是$n_k$不属于已选择的集合。我们将这条边加入最后的生成树中会出现一个环，则环的一端是$n_k$，此时我们能找到与$n_k$相邻的边的权值比这条边大（因为当时未连接$n_k$时，我们的这条边是最小的），把它去掉我们就能得到一个代价更小的生成树，且是连通的。
所以，我们的贪心选择是最优的。但是，最小生成树不是唯一的，因为在某个步骤会出现多个权值相同的最小边，此时，最小边选择不同，可能导致最小生成树不同。

2.3 算法实现

为了记录从 $U$ 到 $V-U$ 具有最小代价的边，我们可以设一个辅助数组closedge。对每一个顶点$v_i\in V-U$,在辅助数组中存在一个相应分量closedge[i-1]，它包括两个域：

• lowcost存储该最小边上的权值，即
  $$closedge[i-1].lowcost=Min\{cost(u,v_i)|u\in U\}$$
• vex域存储该边依附的在U中的顶点。

即如下这种数据结构：

有了这个数组，我们可以从某一顶点u出发，然后closedge中其他顶点$v_i$的的lowcost初始化为 $u到v_i$ 的边上权值，U中附加点的位置就是$u$在U中的位置。
初始化后，我们就可以利用上述的贪心准则逐步构造我们的最小生成树，即每次从closedge中选择一个不构成环的最小顶点，记住每选择一个$v$并入U后都要更新数组closedge，因为此时U更新了，而closedge是U中顶点到其他顶点的最小值，是不断更新的。

每当加入一个顶点v到U时，我们将closedge[v-1].cost赋成0，表示已加入顶点集

// 无向带权图的普里姆算法
void MST_Prim(Graph G, string v) {
	// 用普里姆算法从顶点v出发构造网G的最小生成树T，并输出T的各条边
	// 记录顶点集U到V-U的代价最小的边的辅助数组定义
	struct arcnode{
		string adjvex; // U中的尾点
		int lowcost;   // 对应的最小代价
	}closedge[MAX_VERTEX_NUM];
	int k = LocateVex(G, v); //v在G中的位置
	int i;
	for (i = 0; i < G.vexnum; i++) { //辅助数组初始化
		if (i != k) {
			closedge[i] = {v,G.arcs[k][i].adj};
		} 
	}
	closedge[k].lowcost = 0;  // 初始U={vk},即先并入顶点v
	for (i = 1; i < G.vexnum; i++) { // 选择其余G.vexnum-1个顶点
		// 在数组closedge中找到数组最小的元素对应的下标，且其对应元素值不为0
		int min = 0;
		for (int j = 0; j < G.vexnum; j++) {
			if ((closedge[j].lowcost < closedge[min].lowcost && closedge[j].lowcost) || closedge[min].lowcost == 0) min = j;
		}
		cout << "(" << closedge[min].adjvex << "," << G.vexs[min] << "),";
		closedge[min].lowcost = 0;  // 将vmin并入U
		for (int j = 0; j < G.vexnum; j++) { // 更新辅助矩阵
			if (G.arcs[min][j].adj < closedge[j].lowcost) {
				closedge[j] = { G.vexs[min],G.arcs[min][j].adj };
			}
		}
	}
}

由于我们每次找的是closedge[].cost=0的点，即不在生成树中的点，所以不会产生环路。

2.4 时间复杂度

假设网中有n个顶点，第一个进行初始化的频度为n，第二个循环语句的频度为n-1，其中有两个内循环：其一、在closedge.lowcost中查找最小元素，其频度为n-1；其二是更新最小代价的边，其频度为n。
因此，普里姆算法的时间复杂度为$O(n^2)$，与网中的边无关，适合求边稠密的网的最小生成树。

2.5 测试代码

我们用如下连通网进行测试，且用邻接矩阵来存储图。

#include 
#include 

using namespace std;

#define MAX_VERTEX_NUM 20   // 最大的顶点数
// 弧的基本结构的定义
typedef struct ArcCell {
	int adj;  // 表示该弧上的权值
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
// 带权图的基本结构
typedef struct {
	int vexnum, arcnum;         //当前的顶点数和边数
	AdjMatrix arcs;             // 邻接矩阵
	string vexs[MAX_VERTEX_NUM];  // 顶点矩阵
}Graph;
// 无向带权图的普里姆算法
void MST_Prim(Graph G, string v);
int LocateVex(Graph G, string v) { // 在图G中找顶点v的位置
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != v; i++);
	if (i == G.vexnum) return -1;
	else return i;
}
void createGraph(Graph& G) {
	printf("输入图的顶点数和边数：\n");
	cin >> G.vexnum >> G.arcnum;
	printf("输入图的顶点信息:\n");
	for (int i = 0; i < G.vexnum; i++) cin >> G.vexs[i];
	for (int i = 0; i < G.vexnum; i++) { // 初始化邻接矩阵
		for (int j = 0; j < G.vexnum; j++) G.arcs[i][j].adj = INT_MAX;
	}
	printf("输入图的边信息vi-vj-weight:\n");
	string v1, v2;
	int cost;
	for (int i = 0; i < G.arcnum; i++) {
		cin >> v1 >> v2 >> cost;
		int l1 = LocateVex(G, v1);
		int l2 = LocateVex(G, v2);
		G.arcs[l1][l2].adj = G.arcs[l2][l1].adj = cost;
	}
}

测试输入：

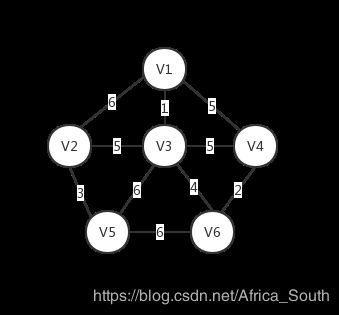
6 10
V1 V2 V3 V4 V5 V6
V1 V2 6
V1 V3 1
V1 V4 5
V2 V3 5
V2 V5 3
V3 V4 5
V3 V5 6
V3 V6 4
V4 V6 2
V5 V6 6

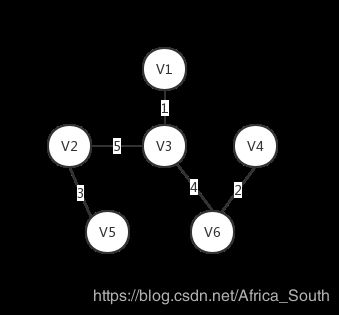
测试输出：

(V1,V3),(V3,V6),(V6,V4),(V3,V2),(V2,V5)

模拟的过程

辅助数组变化过程

即最后的生成树：

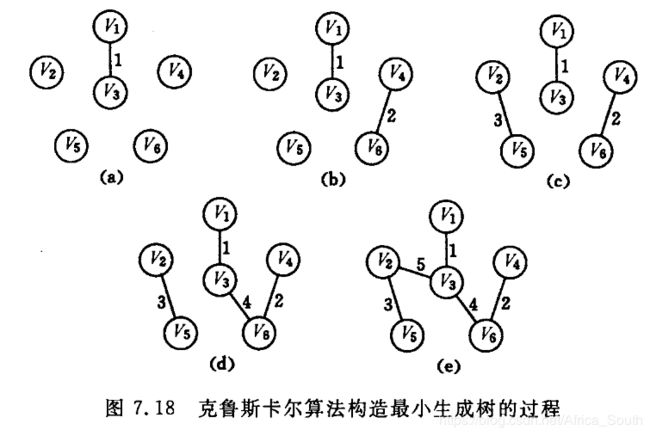
3.克鲁斯卡尔算法（kruskal）

3.1 算法流程

假设连通图$N=(V,\{E\})$。

• 1).令最小生成树的初始状态为只有n个顶点而无边的非连通图$T=(V,\{\})$。图中的每一个顶点自成一个连通分量，若把各个顶点看成一棵树的根节点，则T是一个含有$n$棵树的森林；
• 2).在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。
• 3).依次类推，直到T中所有顶点在同一连通分量上。

简单来说，Prime算法从点出发，克鲁斯卡尔算法从边出发，不断选择一条代价最小的边且加入不会构成环的，将其两端点并入生成树顶点集T。

举个栗子

3.2 算法正确性证明

和2.2一样，使用反证法。

3.3 算法实现

难点一：
对带权值的边进行排序？
该算法至多对$e$条边各扫描依次，假若用小根堆来存放网中的边，则每次选择最小代价的边仅需$O(loge)$的时间（第一次需要$O(e)$）。当然，用其他的排序算法也是可以的，这里，我是用的是C++STL中的sort函数。
难题二：
如何判断加入边$(u,v)$后不会产生环？
使用并查集。生成树T的每个连通分量可以看成是一个等价类，则构造T加入新的边的过程类似于求等价类的过程，等价关系是结点间是否有路径连通。

#include 
#include 
#include 

using namespace std;

// ---- 树的双亲表存储表示 ----
#define MAX_NODE_NUM 20
#define MAX_EDGE_NUM 20
typedef string ElemType;
typedef struct PTNode{ // 结点结构
	ElemType data;
	int parent; // 双亲位置域
}PTnode;
typedef struct { // 树结构
	PTnode nodes[MAX_NODE_NUM];
	int n;       // 结点数
}PTree;
//---- MFSet的树的双亲存储表示 ----
typedef PTree MFSet;
// ---- 树的结构定义 ----
typedef struct edge {
	int begin;
	int end;
	int cost;
}Edge;  // 边结点定义
typedef struct MGraph {
	Edge edges[MAX_EDGE_NUM];  // 边数组
	string vexs[MAX_NODE_NUM]; // 结点数组
	int arcnum, vexnum;        // 当前结点和边数
}MGraph;
int Locate(MGraph G, string u); // 返回u在G中的位置
void createGraph(MGraph& G, MFSet& S); // 创建图G,同时初始化并查集s
int mix_merge(MFSet& s, int i, int j); // 合并i和j所在子树
int mix_find(MFSet& s, int i); // 查找i所在子树的根结点
int Locate_node(MFSet s, string u); //包含信息u的结点的位置
int cmp(Edge e1, Edge e2) {
	return e1.cost < e2.cost;
}
void MST_Kruscal(MGraph G, MFSet s); //最小生成树的克鲁斯卡尔算法
int main() {
	MGraph G;
	MFSet S;
	createGraph(G, S);
	MST_Kruscal(G, S);

	system("pause");
	return 0;
}
void MST_Kruscal(MGraph G, MFSet s) {
	int vexn = G.vexnum;
	int arcn = G.arcnum;
	sort(G.edges, &G.edges[arcn - 1], cmp); // 先对边结点进行排序
	int i;
	for (i = 0; i < arcn; i++) {
		int v1 = G.edges[i].begin;
		int v2 = G.edges[i].end;
		int r1 = mix_find(s, v1);
		int r2 = mix_find(s, v2);
		if (r1 != r2 ) { // 两个顶点和合并
			cout << "(" << G.vexs[v1] << "," << G.vexs[v2] << ") " << G.edges[i].cost << endl;;
			mix_merge(s, r1, r2); // 注意合并的一定是根节点
		}
	}
}
int Locate_node(MFSet s, string u) {
	int i;
	for (i = 0; i < s.n && s.nodes[i].data != u; i++);
	if (i == s.n) return -1;
	else return i;
}
int Locate(MGraph G, string u) {
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != u; i++);
	if (i == G.vexnum) return -1;
	else return i;
}
void createGraph(MGraph& G,MFSet& S) {
	printf("输入图的顶点数和边数:\n");
	cin >> G.vexnum >> G.arcnum;
	S.n = G.vexnum; // 结点数目
	printf("输入图的顶点信息:\n");
	int i;
	for (i = 0; i < G.vexnum; i++) {
		cin >> G.vexs[i];
		S.nodes[i].data = G.vexs[i];
		S.nodes[i].parent = -1;
	} 
	printf("以vi vj cost的形式输入边:\n");
	for (i = 0; i < G.arcnum; i++) {
		string v1, v2;
		int weight;
		cin >> v1 >> v2 >> weight;
		int l1 = Locate(G, v1);
		int l2 = Locate(G, v2);
		G.edges[i].begin = l1;
		G.edges[i].end = l2;
		G.edges[i].cost = weight;
	}
}

int mix_merge(MFSet& s, int i, int j) {
	// i和j分别是两个子集si和sj的根节点
	if (i < 0 || i>s.n || j<0 || j>s.n) return 0; //输入有误
	if (s.nodes[i].parent > s.nodes[j].parent) { // i的成员少
		s.nodes[j].parent += s.nodes[i].parent;
		s.nodes[i].parent = j;
	}
	else {
		s.nodes[i].parent += s.nodes[j].parent;
		s.nodes[j].parent = i;
	}
	return 1;
}
int mix_find(MFSet& s, int i) {
	// 确定i所在子集，并将从到根路径上的所有结点变成根的孩子结点
	if (i < 0 || i > s.n) return -1; // 根结点编号0到n-1
	int j;
	// 查找i的根结点j
	for (j = i; s.nodes[j].parent >= 0; j = s.nodes[j].parent); // 到-1停止
	int k;
	int t;
	for (k = i; k != j; k = t) {
		t = s.nodes[k].parent;
		s.nodes[k].parent = j;
	}
	return j;
}

测试输入：
与2.5用同一连通网：

6 10
V1 V2 V3 V4 V5 V6
V1 V2 6
V1 V3 1
V1 V4 5
V2 V3 5
V2 V5 3
V3 V4 5
V3 V5 6
V3 V6 4
V4 V6 2
V5 V6 6

上述并查集也可以用数组来模拟，看起来简洁一点.
并查集——数组模拟

输出结果一致！！
注意两点：

• 顶点下标从0到n-1；
• 每次合并不同连通分量的时候，一定是合并根结点。

参考资料

《数据结构 C语言描述》 严蔚敏著