剑指Offer and Leetcode刷题总结之三:树
目录
剑指07:重建二叉树/Leetcode105||树||递归(待完成)
剑指26:树的子结构(题解参考)||树||递归
剑指27:二叉树的镜像/Leetcode226||树||递归
剑指28:对称的二叉树/Leetcode101||树||递归
剑指32-I:从上到下打印二叉树(即层序遍历,输出为一维数组)
剑指32-II:从上到下打印二叉树II/Leetcode102(即层序遍历,输出为二维数组)
Leetcode107:二叉树的层次遍历II(Bottom-up层次遍历,输出为二维数组)
剑指32-III:从上到下打印二叉树III/Leetcode103(zigzag遍历,输出为二维数组)
剑指33:二叉搜索树的后序遍历序列||树||递归
Leetcode111:二叉树的最小深度||递归
Leetcode112:路径总和||递归
剑指34:二叉树中和为某一值的路径/Leetcode113:路径总和2||递归(Lc111/Lc112/Lc113类似)
剑指37:序列二叉树(待完成)
剑指54:二叉搜索树的第K大节点
剑指55-I:二叉树的深度
剑指55-II:平衡二叉树
剑指68-I:二叉搜索树的最近公共祖先(题解参考)/Leetcode235||树||递归
剑指68-II:二叉树的最近公共祖先(题解参考)/Leetcode236||树||递归
Leetcode98:验证二叉搜索树
Leetcode100:相同的树
Leetcode105:从前序与中序遍历序列构造二叉树
Leetcode108:将有序数组转换为二叉搜索树(题解参考)
Leetcode144:二叉树的前序遍历
Leetcode543:二叉树的直径
Leetcode662:二叉树的最大宽度
Leetcode958:二叉树的完全性检验
剑指07:重建二叉树/Leetcode105||树||递归(待完成)
剑指26:树的子结构(题解参考)||树||递归
题目:输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构);B是A的子结构, 即 A中有出现和B相同的结构和节点值。
基本思路:利用helpfunction:isSubtree(A,B)判断B树被A树包含,且B的root和A的root重合;
class Solution26(object):
def isSubStructure(self, A, B):
def isSubTree(A, B):
"""
以A节点为root的Tree是否包含以B节点为root的Tree,root为两者的公共node
"""
if not B: return True # 原始的B不为None, 在主函数中已经做了限制;B被遍历完了
if not A: return False # A树先被遍历完成,False
if A.val == B.val:
return isSubTree(A.left, B.left) and isSubTree(A.right, B.right)
return False
if not A or not B: return False
# 要么从节点A开始,B树就开始能匹配上;要么B在A.left的structure里,要么在A.right的structure里
return isSubTree(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B)剑指27:二叉树的镜像/Leetcode226||树||递归
题目:请完成一个函数,输入一个二叉树,该函数输出它的镜像。
基本思路:直接递归,别多想;
时间复杂度O(N):其中N为二叉树的节点数量,建立二叉树镜像需要遍历树的所有节点,占用O(N)时间。
空间复杂度O(N):最差情况下(当二叉树退化为链表),递归时系统需使用O(N)大小的栈空间。
class Solution27(object):
"""
总结:递归的关键就是不要想太多,假设mirrorTree(root.right),mirrorTree(root.left)是已经完成的结果;
!最后要返回root这个结果!
???递归的时间和空间复杂度如何分析???
"""
def mirrorTree(self, root):
if not root: return root
root.left, root.right = self.mirrorTree(root.right), self.mirrorTree(root.left)
return root剑指28:对称的二叉树/Leetcode101||树||递归
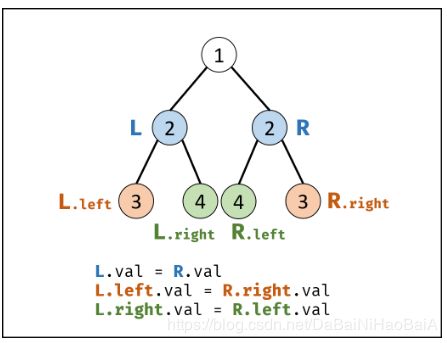
题目:请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
基本思路:递归;利用helpfunction(L, R),需要判断L和R两棵子树是否对称;继而判断L.left and R.right是否对称;
class Solution28(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
def recur(L, R):
if not L and not R: return True # 同时为None, 则返回True
# L和R不同时为None, L为None或者R为None, 或者L!=R,then return False
if not L or not R or L.val != R.val: return False
return recur(L.left, R.right) and recur(L.right, R.left)
if not root: return True
return recur(root.left, root.right)剑指32-I:从上到下打印二叉树(即层序遍历,输出为一维数组)
基本思路:直接层序遍历
class Solution(object):
"""
方法1:
层序遍历
"""
def levelOrder(self, root):
if not root: return []
ans = []
level = [root]
while level:
tmp = []
for node in level:
ans.append(node.val)
if node.left: tmp.append(node.left)
if node.right:tmp.append(node.right)
level = tmp
return ans剑指32-II:从上到下打印二叉树II/Leetcode102(即层序遍历,输出为二维数组)
class Solution32(object):
"""
方法1:层序遍历
时间复杂度:遍历tree中所有节点,O(n)
空间复杂度:最差情况,为平衡二叉树,最多有N/2 tree nodes在queue中,O(n)
"""
def levelOrder(self, root):
if not root: return []
ans = []
level = [root]
while level:
ans.append([i.val for i in level])
tmp = []
for node in level:
if node.left: tmp.append(node.left)
if node.right:tmp.append(node.right)
level = tmp
return ans
"""
方法2:依然是层序遍历(一定要学会借助队列的思想queue)
时间和空间复杂度跟方法1分析相同;
"""
def levelOrder_02(self, root):
from collections import deque
if not root: return []
ans = [] # 定义结果输出
queue = deque()
queue.append(root)
while queue:
tmp = []
for _ in range(len(queue)):
node = queue.popleft()
tmp.append(node.val)
if node.left: queue.append(node.left)
if node.right:queue.append(node.right)
ans.append(tmp)
return ansLeetcode107:二叉树的层次遍历II(Bottom-up层次遍历,输出为二维数组)
基本思路:最后反转ans即可
class Solution(object):
def levelOrderBottom(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root: return []
level = [root]
ans = []
while level:
tmp = []
val = []
for node in level:
val.append(node.val)
if node.left: tmp.append(node.left)
if node.right:tmp.append(node.right)
ans.append(val)
level = tmp
return ans[::-1]剑指32-III:从上到下打印二叉树III/Leetcode103(zigzag遍历,输出为二维数组)
基本思路:判断奇偶数,反转当前打印结果
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root: return []
level = [root]
ans = []
depth = 0
while level:
val = []
tmp = []
for node in level:
val.append(node.val)
if node.left: tmp.append(node.left)
if node.right:tmp.append(node.right)
level = tmp
if depth % 2 == 1:
ans.append(val[::-1])
else:
ans.append(val)
depth += 1
return ans剑指33:二叉搜索树的后序遍历序列||树||递归
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
基本思路:后续遍历序列,数组最后一个值为root,再根据搜索树的大小关系找到分界点。在两个数组里再分别递归;
class Solution33(object):
"""
时间复杂度O(N^2):每次调用2个verifyPostorder,达到减去一个根节点的目的,因此递归占用 O(N);最差情况下(即当树退化为链表),每轮递归都需遍历树所有节点,占用O(N)
空间复杂度O(N):最差情况下(即当树退化为链表),递归深度将达到N 。
"""
def verifyPostorder(self, postorder):
if not postorder: return True # 根据题目来
size = len(postorder)
root = postorder[-1] # 拿掉最后一个元素/node,对应着root
# for i in range(size - 1):
for i in range(size):
if postorder[i] > root: break # 找到二叉树分界点
# for j in range(i, size - 1):
for j in range(i, size):
if postorder[j] < root: return False
left = True
if i > 0: # 首先要判断是否存在左分支,i大于0就一定会有左分支;等价对应着[0:i]有意义
left = self.verifyPostorder(postorder[0:i])
right = True
if i < size - 1: # 判断是否有右分支;也等价对应着[i:size-1]有意义
right = self.verifyPostorder(postorder[i:size-1])
return left and rightLeetcode111:二叉树的最小深度||递归
题目:给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
基本思路:
1. root是否为None;
2. 分别对Left and Right进行递归;
2. Left和Right node情况;有一侧为None,那么只需要考虑另外一侧;如果同时不为None,那么取小的一侧;
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0 # 为空
if not root.left and not root.right: return 1 # 自己即为叶节点
left_dep = self.minDepth(root.left)
right_dep= self.minDepth(root.right)
# 其中有一个为空,总深度则为另一侧的深度+1
if not left_dep or not right_dep: return left_dep + right_dep + 1
# 两侧都不为空
return min(left_dep + 1, right_dep + 1)Leetcode112:路径总和||递归
基本思路:此题返回的是Boolean;Lc113返回的是具体list;
1. root是否为None
2. root没有子节点,且本身val即为所求值;
3. Left and Right双侧递归
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if not root: return False
if not root.left and not root.right and sum == root.val: return True
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)剑指34:二叉树中和为某一值的路径/Leetcode113:路径总和2||递归(Lc111/Lc112/Lc113类似)
基本思路:层序遍历+stack(记录每一个节点node,以及当前的路径和,以及当前的路径list)[(node, node.val, track)]
class Solution(object):
def pathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: List[List[int]]
"""
if not root: return []
stack = [(root, root.val, [root.val])]
ans = []
while stack:
node, val, track = stack.pop()
# 到了叶子节点需要做一次判断
if not node.left and not node.right and val == sum:
ans.append(track)
# 左右节点不为None时,append(node, 截止到当前的sum, 以及截止到当前的路径))
if node.left:
stack.append((node.left, node.left.val + val, track + [node.left.val]))
if node.right:
stack.append((node.right, node.right.val + val, track + [node.right.val]))
return ans剑指37:序列二叉树(待完成)
剑指54:二叉搜索树的第K大节点
基本思路:数的中序遍历输出之后,取的倒数第K个元素即可
class Solution(object):
"""
方法1:数的中序遍历输出之后,取的倒数第K个元素即可
时间复杂度为O(n):n为nodes的个数,每个点都要循环一遍
"""
def kthLargest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
# if not root: return None
stack = [(False, root)]
ans = []
while stack:
mark, node = stack.pop()
if not node: continue
if mark:
ans.append(node.val)
else:
stack.append((False, node.right))
stack.append((True, node))
stack.append((False, node.left))
return ans[-k]剑指55-I:二叉树的深度
class Solution55(object):
"""
recursion function:maxDepth = 1 + max(maxDepth(left) + maxDepth(right))
base condition:
if root = None: return 0
if root.left = None and root.right = None: return 1
"""
"""
方法1:深度优先搜索中的(DFS)
时间复杂度O(n),需要遍历所有节点;
当退化为链表时,递归深度为n, 需要用来存储变量的空间为n(每个return都需要一个申明一个空间用来存储返回值),空间复杂度O(n)
"""
def maxDepth(self, root):
if root == None:
return 0
if root.left == None and root.right == None: # 这个条件也可以去掉,因为max(maxDepth(root.left), maxDepth(root.right))也可以返回0,包含这种情况;
return 1
return 1 + max(maxDepth(root.left), maxDepth(root.right))
"""
方法2:广度优先搜索中的(BFS)--层序遍历
时间复杂度O(n),需要遍历所有节点;
当退化为链表时,递归深度为n, 需要用来存储变量的空间为n(每个return都需要一个申明一个空间用来存储返回值),空间复杂度O(n)
"""
def maxDepth_02(self, root):
if not root: return 0
dep = 0 # depth
queue = [root]
while queue:
layer = []
dep += 1
for node in queue:
if node.left: layer.append(node.left)
if node.right:layer.append(node.right)
queue = layer
return dep剑指55-II:平衡二叉树
基本思路:左右子树深度差不大于1 and 左子树是平衡二叉树 and 右子树是平衡二叉树(求深度helpfuntion,递归两行代码搞定)
class Solution(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
# 递归求深度/还可以用层序遍历,非递归求深度
def depth(root):
if not root: return 0
# if not root.left and not root.right: return 1 # 这一句不必,root非none,深度至少为1
return 1 + max(depth(root.left),(depth(root.right)))
if not root: return True
# 不能这样写的原因是,不仅左子树和右子树深度差不大于1,左右子树中的所有节点的左右子树的深度差都不能大于1
# if abs(depth(root.left) - depth(root.right)) <= 1: return True
return abs(depth(root.left) - depth(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)
剑指68-I:二叉搜索树的最近公共祖先(题解参考)/Leetcode235||树||递归
基本思路:两个node分列在两侧即为最近公共祖先,因为是搜索树,直接比大小即可 1.迭代 2.递归
class Solution68(object):
"""
方法1:递归
时间复杂度 O(N): 其中N为二叉树节点数;每循环一轮排除一层,二叉搜索树的层数最小为logN(满二叉树),最大为N(退化为链表)。
空间复杂度 O(N): 最差情况下,即树退化为链表时,递归深度达到树的层数N。
"""
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
# 题干有说明,所有节点的值均唯一 and q, p为不同节点且存在二叉树中
# 所以不为root不为None
if p.val < root.val and q.val < root.val:
return self.lowestCommonAncestor(root.left, p, q)
if p.val > root.val and q.val > root.val:
return self.lowestCommonAncestor(root.right, p, q)
# else, p and q在root的异侧
return root
"""
方法2:迭代
时间复杂度 O(N):其中N为二叉树节点数;每循环一轮排除一层,二叉搜索树的层数最小为logN(满二叉树),最大为N(退化为链表)。
空间复杂度 O(1):使用常数大小的额外空间。
"""
def lowestCommonAncestor(self, root, p, q):
while root:
if p.val < root.val and q.val < root.val:
root = root.left
elif p.val > root.val and q.val > root.val:
root = root.right
else:
break
return root剑指68-II:二叉树的最近公共祖先(题解参考)/Leetcode236||树||递归
基本思路:递归
时间复杂度O(N) : 其中 NN 为二叉树节点数;最差情况下,需要递归遍历树的所有节点。
空间复杂度O(N) : 最差情况下,递归深度达到N ,系统使用O(N)大小的额外空间。
1. root为空的时候返回 2. root == p or root == q时,返回root;
2. left and right分别递归找节点;
3. 如果left没找到,那么在right中;right没找到,则在left中;
4. left和right都不为空,那么说明p和q在root两侧,即为需要求的值;
class Solution_68(object):
def lowestCommonAncestor(self, root, p, q):
# 题干有说明,所有节点的值均唯一 and q, p为不同节点且存在二叉树中
if not root or root == p or root == q: return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left: return right
if not right: return left
return rootLeetcode98:验证二叉搜索树
基本思路:中序遍历之后,判断是否为升序序列;OR在遍历的同时就check append的数是否大于已遍历list中的最后一个元素
中序遍历时间复杂度O(n)
class Solution(object):
"""
方法1:中序遍历之后,判断是否为升序序列
中序遍历时间复杂度O(n)
判断升序序列时间复杂度O(n))
"""
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root: return True
ans = []
stack = [(False, root)]
while stack:
mark, node = stack.pop()
if not node: continue
if mark:
if not ans or (len(ans) != 0 and node.val > ans[-1]):
ans.append(node.val)
else:
return False
else:
stack.append((False, node.right))
stack.append((True, node))
stack.append((False, node.left))
return TrueLeetcode100:相同的树
题目:给定两个二叉树,编写一个函数来检验它们是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
基本思路:1. 都为None,return True;-->2. 至少一个不为None,任意一个为None,return False;-->均不为None:node.val相同 and left = left and right = right;
class Solution(object):
def isSameTree(self, p, q):
"""
:type p: TreeNode
:type q: TreeNode
:rtype: bool
"""
if not p and not q: return True
if not p or not q: return False
return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)Leetcode105:从前序与中序遍历序列构造二叉树
基本思路:
前序遍历首元素3为root,在中序遍历中找到root的index为1,则数组中preorder[ :1+1] and inorder[ :1+1]表示左子树+root的所有nodes。再继续对左子树和右子树分别建树即可;
优化:在inorder查找root时,每次时间复杂度O(n),n为inorder长度,可建立hashmap;空间换时间;
时间复杂度O(logn):n为inorder长度,为递归深度;
空间复杂度O(n):n为inorder长度
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
if len(preorder) == 0: return None
root = TreeNode(preorder[0]) # 前序遍历第一个元素即为root
# 在中序遍历中,找到根节点的位置
# mid = inorder.index(preorder[0]) # 每次要在inorder中遍历,优化:存在hashmap里
dict = {}
for ind, val in enumerate(inorder):
dict[val] = ind
mid = dict.get(preorder[0])
root.left = self.buildTree(preorder[1:mid+1], inorder[ :mid])
root.right = self.buildTree(preorder[mid+1: ], inorder[mid+1: ])
return rootLeetcode108:将有序数组转换为二叉搜索树(题解参考)
基本思路:找到中点,分为左子树和右子树,分别递归
时间复杂度:O(n) -- 每个元素都访问一次(待理解)
空间复杂度:O(logn) -- 递归调用函数栈所需要的空间
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums: return None
size = len(nums)
mid = size // 2 # 将数组均分,size为偶数则取右边的数;奇数则取中间
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[ :mid])
root.right = self.sortedArrayToBST(nums[mid+1: ])
return rootLeetcode144:二叉树的前序遍历
题目:给定一个二叉树,返回它的 前序 遍历。
基本思路:1. 递归;2. 非递归;
class Solution(object):
"""
方法1:递归方式
"""
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
ans = []
def dfs(root):
if not root: return
ans.append(root.val)
dfs(root.left)
dfs(root.right)
dfs(root)
return ans
"""
方法2:非递归方式
"""
def preorderTraversal(self, root):
if not root: return []
stack = [(False, root)]
ans = []
while stack:
mark, node = stack.pop()
if not node: continue
if mark:
ans.append(node.val)
else:
stack.append((False, node.right))
stack.append((False, node.left))
stack.append((True, node))
return ansLeetcode543:二叉树的直径
题目:给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
基本思路:需要维护一个全局变量,然后在求树的深度过程中,不断更新节点之间的最长距离
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def diameterOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
self.depth(root)
return self.max
# 需要维护一个全局变量来更细max
def __init__(self):
self.max = 0
# 再求深度的过程中,不断更新max
def depth(self, root):
if not root: return 0
left = self.depth(root.left)
right = self.depth(root.right)
self.max = max(self.max, left + right) # 更新max
return max(left, right) + 1 # 返回root的深度Leetcode662:二叉树的最大宽度
基本思路:不能单纯的层序遍历,中间包含null也需要count进入width,所以关键是记录每个node的index
如果root从1开始:left node = 2 * index and right node = 2 * index + 1
如果root从0开始:left node = 2 * index + 1 and right node = 2 * index + 2
class Solution(object):
def widthOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root: return 0
level = [(root, 1)]
width = 0
while level:
width = max(width, level[-1][1] - level[0][1] + 1)
tmp = []
for node in level:
node, index = node
if node.left: tmp.append((node.left, 2 * index))
if node.right:tmp.append((node.right, 2 * index + 1))
# width = max(width, tmp[-1][1] - tmp[0][1] + 1) # 这样写不行,因为node可能是叶节点,left and right都为null, 此时tmp是空,所以会报错 out of index
level = tmp
return widthLeetcode958:二叉树的完全性检验
题目:给定一个二叉树,确定它是否是一个完全二叉树。
基本思路:层次遍历,null也要都打印出来,找到第一个null之后,记录index,确保之后全都是null才return True;
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def isCompleteTree(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root: return root
level = [root]
ans = []
while level:
tmp = []
while level:
node = level.pop(0)
if node:
ans.append(node.val)
tmp.append(node.left)
tmp.append(node.right)
else:
ans.append(node)
level = tmp
# print(ans)
for i in range(len(ans)):
if not ans[i]:
inx = i
break
for i in range(inx+1, len(ans)):
if ans[i]: return False
return True