JZOJ-senior-5886. 【NOIP2018模拟9.27】军训

Time Limits: 1000 ms Memory Limits: 262144 KB

Description

小L正在参加学校组织的军训。军训的操场是一个n*m的网格，每个网格开始时都没有人。每次军官会指定某些行和列，并在这些行和列的每个交界处都安排站上一名学生。但为了防止两名学生站到同一个网格中，军官每次指定的行和列并不会和之前指定过的重复。军官接到了上级的要求，需要将学生摆成特定的图案，那么军官能否达成要求呢？

Input

第一行一个整数T，表示数据组数。
接下来每个数据第一行两个整数n,m,意义如题面所述。
接下来n行，每行一个长度为n的字符串,其中第j个字符是’#’则代表i行j列的网格上要有学生，如果是’.’则代表没有。

Output

对于每组数据一行一个字符串“Yes”或者”No”，表示能否达到要求。

Sample Input

1
5 8
.#.#…#.
…#…
.#.#…#.
#.#…#
…#…

Sample Output

Yes

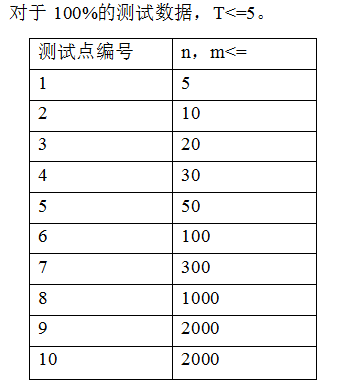
Data Constraint

Solution

题目大意：有一个图案，每次选出一些行和列，行列相交处站人，每行每列都只能选一次，问能否摆成特定图案。

算法一：
通过观察可以发现，图案上的某一个矩形，如果其中3点有人，而另一点没有，那么答案显然就是no，这样暴力，时间复杂度 $O(T\ast N^4)$ ，期望得分50

算法二：
同一行内有人的列肯定是在同一次内被选择，那么我们先暴力将同一行内有站人的列用并查集并起来，表示它们要在同一次内选择，用c[i]表示第i行站人的个数，s[i]表示某个连通块里元素的个数，l[i]表示第i行最后出现有人的位置所在的列，之后从上往下枚举每一行，对于第i行，查询当前c[i]与当前某个有站人的列（为了方便，直接用l[i]就好了）所在并查集的s[i]，如果不相等，那么说明在第i行以下的某一列中有人站在了当前行不站人的列上，那么这是不合法的，时间复杂度 $O(T\ast N^2)$ ，期望得分100

算法三：
我的考场做法，比起算法二要麻烦些，先将每一行中站人的列连接起来，为了方便处理，我们令l[i][j]表示这个位置左边第一个有人的位置所在的列，u[i][j]表示这个位置往上第一个有人的位置所在的行，c[i]表示当前行的人数，暴力枚举有人的行，如果它所连着的行中有跟枚举的行中列位置不一样的，那么显然是no，就这么暴力，时间复杂度 $O(T\ast N^2)$ ，期望得分100

Code

Algorithm 2

Copy from HLY

#include
#include
#include
#include
#include
#include
#define fo(i,l,r) for(int i=l;i<=r;i++)
using namespace std;
const int N=4010;
int F[N],n,m,siz[N],lst[N],cnt[N];
char s[N][N];
int get(int x)
{
	if(F[x]==x) return x;
	return F[x]=get(F[x]);
}
void merge(int x,int y)
{
	x=get(x);y=get(y);
	if(x==y) return;
	F[x]=y;siz[y]+=siz[x];
}
int gc()
{
	scanf("%d%d\n",&n,&m);
	fo(i,1,m) F[i]=i,siz[i]=1;
	int bj=1;
	fo(i,1,n)
	{
		scanf("%s\n",s[i]+1);
		if(!bj) continue;
		lst[i]=0,cnt[i]=0;
		fo(j,1,m) if(s[i][j]=='#')
		{
			if(lst[i]) merge(j,lst[i]);
			lst[i]=j;cnt[i]++;
		}
	}
	fo(i,1,n) if (cnt[i]!=siz[get(lst[i])])
	{
		int x=get(lst[i]);
		bj=0;break;
	}
	return bj;
}
int main()
{
	freopen("rect.in","r",stdin);
	freopen("rect.out","w",stdout);
	int T;scanf("%d\n",&T);
	while(T--) printf((gc())?"Yes\n":"No\n");

}

Algorithm 3

#include
#include
#include

#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define mem(a,b) memset(a,b,sizeof(a))

using namespace std;

const int N=2e3+5;
int T,n,m;
int ll[N],uu[N],l[N][N],u[N][N];
int bz[N],cnt[N],a[N][N];

int main()
{
	freopen("rect.in","r",stdin);
	freopen("rect.out","w",stdout);
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d\n",&n,&m);
		mem(ll,0),mem(uu,0),mem(bz,0);
		fo(i,1,n)
		{
			cnt[i]=0;
			fo(j,1,m)
			{
				a[i][j]=l[i][j]=u[i][j]=0;
				char ch=getchar();
				if(ch=='.') continue;
				a[i][j]=1,++cnt[i];
				l[i][j]=ll[i],ll[i]=j;
				u[i][j]=uu[j],uu[j]=i;
			}
			scanf("\n");
		}
		int ans=1;
		fo(i,1,n) if(cnt[i])
		{
			int r=ll[i];
			for(int y=r;y;y=l[i][y])
			{
				if(bz[y]) {ans=0; break;}
				bz[y]=1;
			}
			if(!ans) break;
			for(int x=uu[r];x>i;x=u[x][r])
			{
				int ok=1;
				for(int y=r;y;y=l[i][y])
				{
					if(a[x][y]) continue;
					ok=0; break;
				}
				if(ok)
				{
					for(int y=r;y;y=l[i][y]) a[x][y]=0;
					cnt[x]-=cnt[i];
				}
			}
			if(!ans) break;
			cnt[i]=0;
		}
		if(ans) printf("Yes\n"); else printf("No\n");
	}
}