算法分析 | 分支限界法 | (优先队列)旅行商问题

注意,旅行商问题一般有一个默认的起点.

 

一.问题分析

 

1.状态结点的数据类型:

int cl;     表示已走的路程

int id;   表示当前准备判断的结点序号

int x[N];    表示一个最佳策略

 

2.约束条件:下一个结点和当前结点有通路,并且解 < 当前的最优解,并且终点和起点形成回路

3.限界条件:当前状态的最大价值上界 > 当前最优解

 

4.初始条件:进入队列的第一个结点是数组元素[0],已走过的路程=0,下一步该判断结点1:最佳路径是默认值{0,1,2}

cl=0;   id=1;  x[N]={0,1,2,3,4,5....};

 

5.终止循环条件:

解向量序号	0	1	2	3	4	...	N-2	N-1
id	1	2	3	4	5	...	N-1	N

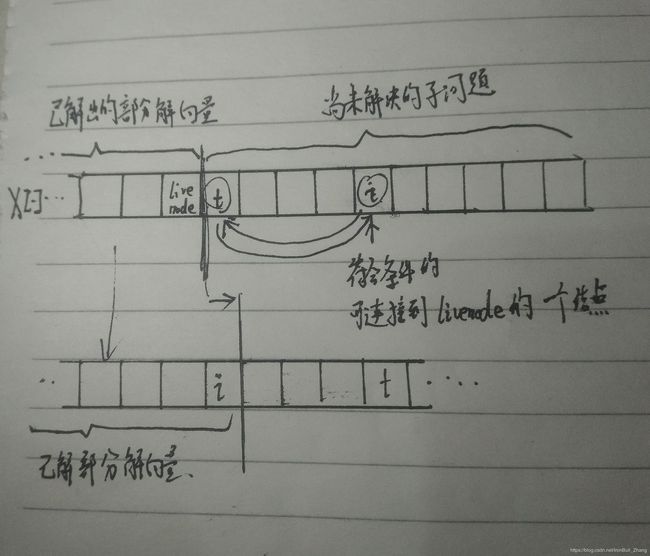
在排列树中,当遍历到倒数第二层(N-2)时,该层结点的子节点只有1个 ,x[N]已完全确定

活结点终止循环(约束)条件为

id==N-1                                                                         //遍历到倒数第二层

T[ livenode.x[ N-1 ]][ livenode.x[ N-2 ]] !=                 //倒数第二个和最后一个联通

T[ 0 ][ livenode.x[ N-1 ] ] !=                                       //最后一个和第一个联通

livenode.cl + T[ livenode.x[ N-1 ]][ livenode.x[ N-2 ]] + T[ 0 ][ livenode.x[ N-1 ] ]

 

 

6.活结点的限界条件:(最优值是最小值的题型,不用写上界函数)

if( livenode.cl > bestp )

    continue;

 7.求全排列的题型中,必定要有swap()存在,将子问题的解从原处交换到队首

 

 

二.代码实现

1.全局变量区

#include"allh.h"
//给定起点

//全局变量
const int N3 = 4;				//城市数量
const int INF = INT_MAX;

vector>T3 ={		//邻接矩阵
{INF,15,30,5},
{15,INF,6,12},
{30,6,INF,3},
{5,12,3,INF },
};

int bestp3;								//记录最优值
vectorbestx3(N3,0);		//记录最优解

//记录状态
struct State2
{
	int cl;			//记录已走过的路程
	int id;		//记录当前判断的结点号

	vector x;

	State2() {};
	State2(int _cl, int _id) {
		cl = _cl;
		id = _id;
		x.resize(N3);
	}

	//结构体组成优先队列,需要写优先函数,该函数不是struct的成员函数,只是作为友元函数写在结构体里
	friend bool operator <(const State2& a, const State2& b)
	{
		return a.cl > b.cl;     //只看符号左边:"怎样的元素优先值更小呢?cl大的数"
	}
};

2.广度遍历函数

double TravelingBFS()
{
	//先压入root结点,让while()开动起来
	int t;		//记录当前物品序号
	State2 livenode, newnode;
	newnode = State2(0, 1);
	for (size_t i = 0; i < N3; i++)
		newnode.x[i] = i;

	priority_queue q2;
	q2.push(newnode);

	//开始循环
	while (!q2.empty())
	{
		livenode = q2.top();
		q2.pop();
		t = livenode.id;

		//活结点的终止循环(约束)条件
		if (t == N3-1                                                         &&	   //到达倒数第二层
		T3[livenode.x[N3 - 2]][livenode.x[N3 - 1]]!=INF  &&      //倒数第二个城市和最后一个城市有连接
		T3[livenode.x[ 0 ]][livenode.x[N3 - 1]] != INF      &&      //最后一个城市和起点城市有连接
		livenode.cl+ T3[livenode.x[N3 - 2]][livenode.x[N3 - 1]]+ T3[livenode.x[ 0 ]][livenode.x[N3 - 1]]= bestp3)
			continue;

		//开始搜索子结点
		for (size_t i = t; i < N3; i++)
		{		
			int cl = livenode.cl + T3[livenode.x[t - 1]][livenode.x[i]];
			//livenode状态下已处理的结点的序号=livenode.id-1
			if (T3[livenode.x[t - 1]][livenode.x[i]] != INF  && cl

3.调用&打印

void TSP()
{
	//初始化
	bestp3 = INF;
	bestx3.resize(N3,0);
	//遍历
	cout<<"最短距离为:		"<

 

三.Bug总结

1.按求解值,分支限界法可分为MAX/MIN两种.本题为最小值的问题,不需要Bound()函数作为限界条件.如果当前值比bestp更大,直接跳过.

2.按最优策略,分支限界法可分为01型和序列型.本题属于序列型,注意swap()的使用