计算机视觉的小tips
这里写自定义目录标题
- 计算机视觉常见小tips及面试经典问题
- 计算参数量以及计算量
- 过拟合要怎么解决?
- 深度学习中激活函数的优缺点
- Batch Normalization 的原理和作用?
- L2正则化的特点和使用场景?
- 正则化为什么可以防止过拟合
- L1正则化损失函数如何求解?
- Loss 优化的几个方法?
- 动量法的表达式?
- 随机梯度下降相比全局梯度下降好处是什么?
- 介绍 Inception-resnet v1?
- 归一化有哪些方式?
- L1、L2正则化在什么任务上分别会优先考虑
- 两层神经网络的权重都是0,bias有值,这个网络能正常训练吗?
- C++和python的区别?
- Python比C++好在哪里?
- python怎么做内存回收?
- 哪种激活函数能缓解梯度爆炸弥散 ?
- Pooling是不是线性操作?
- Dropout介绍
- 输入是特征向量的分类网络,怎么找比较重要的那些特征?
- yolo 介绍?
- 检测任务中解决正负样本不均衡的方法?
- dropout为什么能解决过拟合 ?
- 卷积有哪些变种?
- 手推BP
- 手推RNN和LSTM结构
- pooling作用
- 为什么max pooling要更常用?哪些情况下,average pooling比max pooling更合适?
- 梯度消失和梯度爆炸的原因是什么? 有哪些解决方法?
- CNN和RNN的梯度消失是一样的吗
- relu的负半轴导数都是0,这部分产生的梯度消失怎么办?
- batch size对收敛速度的影响
- 网易面试题:图像处理中边缘检测算法sobel与canny在应用上有什么区别?
- 讲一下AlexNet的具体结构,每层的作用
- 参考链接:
计算机视觉常见小tips及面试经典问题
你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。
计算参数量以及计算量
过拟合要怎么解决?
Dropout(随机失活)、Weight Decay(权重衰减)、减少模型参数、Early Stop、Regularization(正则化,包括L1,L2正则化等)、Augmentation(数据增强)、合成数据、Batch Normalization(批次标准化)、Bagging 和 Boosting(模型融合)等
深度学习中激活函数的优缺点
在深度学习中,信号从一个神经元传入到下一层神经元之前是通过线性叠加来计算的,而进入下一层神经元需要经过非线性的激活函数,继续往下传递,如此循环下去。由于这些非线性函数的反复叠加,才使得神经网络有足够的capacity来抓取复杂的特征。
为什么要使用非线性激活函数?
答:如果不使用激活函数,这种情况下每一层输出都是上一层输入的线性函数。无论神经网络有多少层,输出都是输入的线性函数,这样就和只有一个隐藏层的效果是一样的。这种情况相当于多层感知机(MLP)。
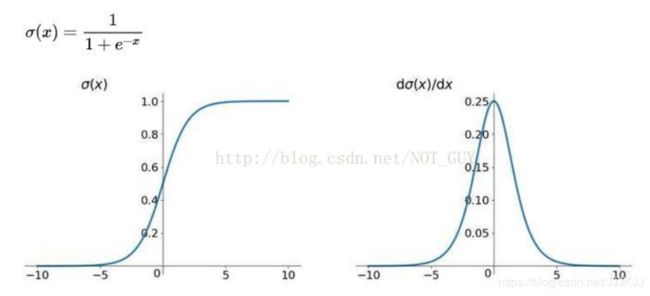
1、Sigmoid函数
优点:
(1)便于求导的平滑函数;
(2)能压缩数据,保证数据幅度不会有问题;
(3)适合用于前向传播。
(4)将线性函数转变为非线性函数。
缺点:(1)容易出现梯度消失(gradient vanishing)的现象:当激活函数接近饱和区时,变化太缓慢,导数接近0,根据后向传递的数学依据是微积分求导的链式法则,当前导数需要之前各层导数的乘积,几个比较小的数相乘,导数结果很接近0,从而无法完成深层网络的训练。
(2)Sigmoid的输出不是0均值(zero-centered)的:这会导致后层的神经元的输入是非0均值的信号,这会对梯度产生影响。以 f=sigmoid(wx+b)为例, 假设输入均为正数(或负数),那么对w的导数总是正数(或负数),这样在反向传播过程中要么都往正方向更新,要么都往负方向更新,导致有一种捆绑效果,使得收敛缓慢。
(3)幂运算相对耗时
2、tanh函数
优点:
(1) Tanh 函数的导数比 Sigmoid 函数导数值更大、梯度变化更快,在训练过程中收敛速度更快;
(2) 使得输出均值为 0,可以提高训练的效率;
(3) 将线性函数转变为非线性函数;
tanh函数将输入值压缩到 -1~1 的范围,因此它是0均值的,解决了Sigmoid函数的非zero-centered问题,但是它也存在梯度消失和幂运算的问题。
缺点:
(1) 幂运算相对来讲比较耗时;
(2) 容易出现梯度消失;
其实 tanh(x)=2sigmoid(2x)-1
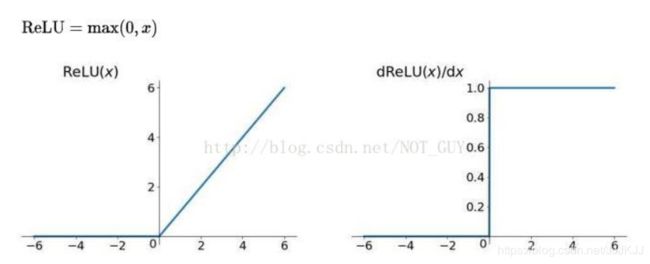
3、ReLU函数:全区间不可导
优点:
(1)ReLu的收敛速度比 sigmoid 和 tanh 快;(梯度不会饱和,解决了梯度消失问题)
(2)计算复杂度低,不需要进行指数运算;
(3)适合用于后向传播。
缺点:
(1)ReLU的输出不是zero-centered;
(2)Dead ReLU Problem(神经元坏死现象):某些神经元可能永远不会被激活,导致相应参数永远不会被更新(在负数部分,梯度为0)。产生这种现象的两个原因:参数初始化问题;learning rate太高导致在训练过程中参数更新太大。 解决方法:采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
(3)ReLU不会对数据做幅度压缩,所以数据的幅度会随着模型层数的增加不断扩张。
4、Leakly ReLU函数
当x<0时,f(x)=αx,其中α非常小,这样可以避免在x<0时,不能够学习的情况:
f(x)=max(αx,x)
称为Parametric Rectifier(PReLU),将 α 作为可学习的参数.
当 α 从高斯分布中随机产生时称为Random Rectifier(RReLU)。
当固定为α=0.01时,是Leaky ReLU。
优点:
不会过拟合(saturate)
计算简单有效
比sigmoid/tanh收敛快
用来解决ReLU带来的神经元坏死的问题,可以将0.01设置成一个变量a,其中a由后向传播学出来。但是其表现并不一定比ReLU好。
5、ELU函数(指数线性函数)
ELU有ReLU的所有优点,并且不会有 Dead ReLU问题,输出的均值接近0(zero-centered)。但是计算量大,其表现并不一定比ReLU好。。
Batch Normalization 的原理和作用?
将一个 batch 的数据变换到均值为 0、方差为 1 的正态分布上,从而使数据分布一致,每层的梯度不会随着网络结构的加深发生太大变化,从而避免发生梯度消失并且加快收敛,同时还有防止过拟合的效果;
BN层的优点。
1)加快训练速度,这样我们就可以使用较大的学习率来训练网络。
2)提高网络的泛化能力。
3)BN层本质上是一个归一化网络层,可以替代局部响应归一化层(LRN层)。
4)可以打乱样本训练顺序(这样就不可能出现同一张照片被多次选择用来训练),防止训练发生偏移。论文中提到可以提高1%的精度。

L2正则化的特点和使用场景?
机器学习中几乎都可以看到损失函数后面会添加一个额外项,常用的额外项一般有两种,一般英文称作 ℓ1-norm 和 ℓ2 -norm,中文称作 L1正则化 和 L2正则化,或者 L1范数 和 L2范数。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。下图是Python中Lasso回归的损失函数,式中加号后面一项![]() 即为L1正则化项。
即为L1正则化项。

下图是Python中Ridge回归的损失函数,式中加号后面一项![]() 即为L2正则化项。
即为L2正则化项。
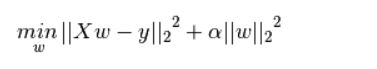
一般回归分析中回归w表示特征的系数,从上式可以看到正则化项是对系数做了处理(限制)。L1正则化和L2正则化的说明如下:
L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为![]()
一般都会在正则化项之前添加一个系数,Python中用α表示,一些文章也用λ表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
详见: https://blog.csdn.net/jinping_shi/article/details/52433975.
正则化为什么可以防止过拟合
详见:正则化为什么可以防止过拟合
L1正则化损失函数如何求解?
参考这一篇:https://www.cnblogs.com/heguanyou/archive/2017/09/23/7582578.html
Loss 优化的几个方法?
主要有三大类:
1.基本梯度下降法,包括 GD,BGD,SGD;
2.动量优化法,包括 Momentum,NAG 等;
3.自适应学习率优化法,包括 Adam,AdaGrad,RMSProp 等
可以看这一篇:各种优化器Optimizer原理:从SGD到AdamOptimizer
动量法的表达式?
随机梯度下降相比全局梯度下降好处是什么?
- 当处理大量数据时,比如SSD或者faster-rcnn等目标检测模型,每个样本都有大量候选框参与训练,这时使用随机梯度下降法能够加快梯度的计算;
- 每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的,并且可以进行在线更新;
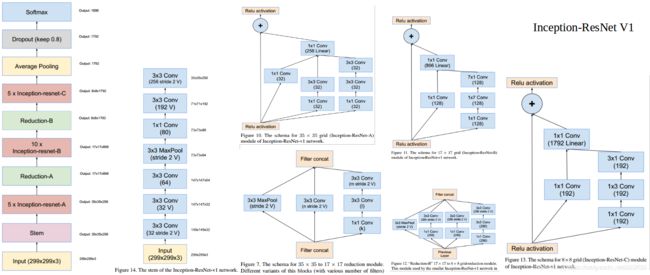
介绍 Inception-resnet v1?
归一化有哪些方式?
min-max 标准化(Min-max normalization):
公式:
x=(x−min)/(max−min)
适用于数据集中的场景,如果 max 和 min 不稳定,很容易使得归一化结果不稳定;
z-score 0均值标准化(zero-mean normalization):
公式:
x=(x−u)/σx
适用场景:
在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,表现更好;
L1、L2正则化在什么任务上分别会优先考虑
假设模型中有很多特征,其中不乏相关性特征,可以用L1消除共线性问题;
在训练样本足够多的情况,然后尝试使用L2来防止过拟合问题;
两层神经网络的权重都是0,bias有值,这个网络能正常训练吗?
不能,因为权重为 0,每次传入不同数据得到的结果相同;
C++和python的区别?
- C++是静态类型的,而python是动态类型的;
- python是一种脚本语言,是解释执行的,不需要经过编译;C++需要编译后运行语言,在特定的机器上编译后在特定的机上运行,运行效率高,安全稳定,但编译后的程序一般是不跨平台的;
- python是逐句解释执行的,C++是先编译成本地代码,期间还有编译期的类型检查,不存在动态类型、动态检查,并且可以进行编译器优化;
Python比C++好在哪里?
自动能实现内存回收机制,开发效率高;
python怎么做内存回收?
当对象不再被引用指向的时候,垃圾收集器可以释放该对象;
手动回收:gc.collect();
哪种激活函数能缓解梯度爆炸弥散 ?
relu、leakrelu、elu 等;
Pooling是不是线性操作?
不是
Dropout介绍
Dropout 是指在模型训练时随机让网络某些隐含层节点的权重不工作,不工作的那些节点可以暂时认为不是网络结构的一部分,但是它的权重得保留下来(只是暂时不更新而已),用于防止模型过拟合;
输入是特征向量的分类网络,怎么找比较重要的那些特征?
使用 SE-Net 的 SE 模块;
yolo 介绍?
检测任务中解决正负样本不均衡的方法?
online hard example mining(OHEM);
Focal Loss;
class balanced cross-entropy;
local rank,PISA,ISR;
过采样;
dropout为什么能解决过拟合 ?
简单的回答是:防止参数过分依赖训练数据,减少神经元之间复杂的共适应关系,增加参数对数据集的泛化能力
卷积有哪些变种?
分组卷积(Group Convolution)、空洞(扩张)卷积(Dilated/Atrous Convolution)、深度可分离卷积(depthwise separable convolution)、可变形卷积网络(Deformable Convolution)、反卷积(deconvolution)、图卷积(Graph Convolution)和 X-卷积(PointCNN);
手推BP
手推RNN和LSTM结构
pooling作用
- 减小计算量
计算量与通道数、特征图长和特征图宽的乘积呈正比,若输入通道数、特征图宽和特征图高分别为c、w、h,则经过stride为2的pooling层,输出为c、w/2、h/2,计算量减小为1/4。
- 减小内存消耗
网络模型的内存消耗与通道数、特征图长和特征图宽的乘积呈正比,若输入通道数、特征图宽和特征图高分别为c、w、h,则经过stride为2的pooling层,输出为n、w/2、h/2,内存消耗量减小为1/4。
- 提高感受野大小
stride>1的pooling可以极大地提高感受野大小,
- 增加平移不变性
为什么max pooling要更常用?哪些情况下,average pooling比max pooling更合适?
Max-pooling和average pooling都对数据进行下采样, 除此之外, max-pooling还提供了非线性, 这是max-pooling效果更好的一个重要原因.
Average pooling并非一无是处, 现在average pooling更多的是用在global average pooling中. 这最早由Network in network提出, 目前在ResNet, GoogLeNet等主流网络中都有使用.
梯度消失和梯度爆炸的原因是什么? 有哪些解决方法?
梯度消失:
1.标准方法来初始化网络中的权重,那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足|wj|<1
2.选择的激活函数。比如sigmoid函数,他的倒数的最大值只有0.5,所以在连乘时导致梯度越来越小。最终消失
梯度爆炸:
当我们将w初始化为一个较大的值时,例如>10的值,那么从输出层到输入层每一层都会有一个s‘(zn)*wn的增倍,当s‘(zn)为0.25时s‘(zn)*wn>2.5,同梯度消失类似,当神经网络很深时,梯度呈指数级增长,最后到输入时,梯度将会非常大,我们会得到一个非常大的权重更新,这就是梯度爆炸的问题,在循环神经网络中最为常见.
解决方案:
-
好的参数初始化方式,如He初始化(Xavier初始化和He初始化)
-
非饱和的激活函数(如 ReLU)
-
批量规范化(Batch Normalization)
-
梯度截断(Gradient Clipping)
-
更快的优化器
-
LSTM
详见:https://blog.csdn.net/junjun150013652/article/details/81274958
CNN和RNN的梯度消失是一样的吗
梯度消失:一句话,RNN梯度消失是因为激活函数tanh函数的倒数在0到1之间,反向传播时更新前面时刻的参数时,当参数W初始化为小于1的数,则多个(tanh函数’ * W)相乘,将导致求得的偏导极小(小于1的数连乘),从而导致梯度消失。
梯度爆炸:当参数初始化为足够大,使得tanh函数的倒数乘以W大于1,则将导致偏导极大(大于1的数连乘),从而导致梯度爆炸。
relu的负半轴导数都是0,这部分产生的梯度消失怎么办?
一旦神经元的激活值进入负半区,则梯度为0,也就是说这个神经元不会经历训练,也就是稀疏性。
虽然热炉在0的时候不可导,但在实现时通常会返回左或者右导数的一个。
batch size对收敛速度的影响
过大:跑完一个epoch迭代次数减少了,但要达到相同的精度,所需的时间大大增加,从而对参数的修正也变得更加缓慢,增大到一定程度,其确定的下降方向已基本不再变化。
过小:由于不同权重的梯度差异值比较大,因此选取一个全局的学习率很困难。
在一定范围内,增大size,其确定的下降方向越准确,引起的震荡越小,有助于提高处理速度,迭代次数降低。
网易面试题:图像处理中边缘检测算法sobel与canny在应用上有什么区别?
答:sobel是基于梯度图像模值大小的检测算子,通常有水平和垂直两种算子。
canny算法实际上是将sobel算子应用两次,取不同于阈值,一个是低阈值,低阈值要包含像素全部的重要边缘,高阈值要尽量将全部的非重要边缘去除。首先进行去噪,寻找亮度梯度,使用滞后阈值进行,canny算子适合于用于不同的场合,不过速度较慢。 它的参数允许根据不同实现的特定要求进行调整以识别不同的边缘特性
sobel算子是其滤波算子的形式,用于提取边缘,可以利用快速卷积函数。但是sobel算子没有将图像主体与背景严格区分开来,没有基于图像灰度进行处理。
讲一下AlexNet的具体结构,每层的作用
参考链接:
https://blog.csdn.net/weixin_44936889/article/details/104606259?fps=1&locationNum=2.
链接: https://blog.csdn.net/not_guy/article/details/78749509.
链接: https://blog.csdn.net/donkey_1993/article/details/81871132.
链接: https://blog.csdn.net/try_again_later/article/details/88536693.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.
链接: link.