基于Python的拓扑排序

什么是拓扑排序？

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列，该序列必须满足下列两个条件：

     1. 每个顶点仅出现一次

     2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

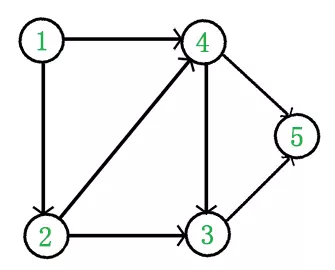
通俗的说，只有有向无环图（DAG）才有拓扑一说，非DAG没有拓扑排序一说。典型的DAG图如下：

 

                                         

 

那么如何对这个有向无环图（DAG）进行拓扑排序呢？

     1. 找出入度数为0的顶点

     2. 将入度数为0的顶点值取出，作为拓扑排序后列表的元素，再将该顶点指向的顶点入度减1

     3. 重复1,2步骤，直到图中没有入度为0且未被访问的顶点，得出的拓扑排序列表即为所求

上图进行拓扑排序的详细图解如下：

 

                   

 

上图经过拓扑排序后的结果为{1 , 2 , 3 , 4 , 5}或者{1 , 2 , 4 , 3 , 5}，值得注意的是，拓扑排序的结果可能不是唯一的，因为可能存在同时入度为0的顶点。

 

拓扑排序的应用场景

一、课程表的安排

     在安排课程表时，有的课程必须基于其他的课程才能学习，例如，学习数据结构与算法之前，必须学习一门编程语言，因为没有编程语言的基础，无法用代码实现数据结构与算法。同理，与其他科目也是如此。这就是典型的有向无环图的一个缩影，在安排课程表时，基于拓扑排序来给学生安排课程，这样才合理。

二、衣服的穿搭

     举个简单的例子，一个人在早上起床时，必须先穿内衣再穿外衣，必须先穿袜子再穿鞋子，必须先穿内裤再穿外裤，这也是拓扑排序的一个缩影，如果穿搭的顺序不按照拓扑排序来进行，会出现非常尴尬的局面，大家脑补！

 

实例（Leecode真题）

问题需求：

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

 

解题思路

     1）、将图进行加工，得到更直观的图。初始化一个列表graph，该列表的元素长度为课程数，列表元素是一个子列表，子列表由三个元素，第一个元素是该顶点的入度数，第二个元素是该顶点的顶点值，第三个元素是包含指向所有的顶点元素的顶点值的列表集合。遍历给出的列表prerequisites，获得第一个元素的值i，j，将graph[i][0]加1，即graph中顶点值为i的子列表的第一个元素（入度数）加1，将graph[j][2].append(i)，即将graph中顶点值为j的顶点指向的顶点列表集合添加顶点值为i的顶点。

     2）、得到加工后的图，定义辅助栈，初始化将graph中入度数为0的顶点压入栈中，再定义一个记录已经访问的顶点的set集合

     3）、以栈不为空作为循环条件，进入循环，弹出栈顶元素，将顶点值添加进拓扑排序表，将其指向的顶点入度数减1；再对graph进行遍历，将入度数为0且顶点值不在记录已经访问的set集合里面的顶点入栈。

     4）、重复第三步，退出循环后，判断拓扑排序表的长度是否等于课程数，若是，则代表拓扑排序成功，若不等于，则代表图不是有向无环图，拓扑排序失败

这个算法的成本较大，有待优化，给出这个算法，是为了更好地让大家理解拓扑排序。话不多说，代码如下：

 

class Solution:
    def canFinish(self, numCourses, prerequisites):
        if prerequisites == []:
            return True
        grap = [[0,_,[]] for _ in range(numCourses)]
        for i in prerequisites:
            grap[i[0]][0]+=1
            grap[i[1]][2].append(i[0])
        queue = []
        visited = set()
        for i in grap:
            if i[0] == 0:
                queue.append(i)
                visited.add(i[1])
        if queue == []:
            return False
        results = []
        while queue:
            cur = queue.pop()
            results.append(cur[1])
            for j in cur[2]:
                grap[j][0]-=1
            for n in grap:
                if n[0]==0 and n[1] not in visited:
                    queue.append(n)
                    visited.add(n[1])
        if len(results) == numCourses:
            return True
        return False