查找算法(Python实现)
查找表
在日常生活中,几乎每天都要进行一些查找的工作,在电话簿中查阅某个人的电话在电脑的文件夹中查找某个具体的文件等等。
查找表是由同一类型的数据元素构成的集合。例如电话号码簿和字典都可以看作是一张查找表。
一般对于查找表有以下几种操作:
- 在查找表中查找某个具体的数据元素;
- 在查找表中插入数据元素;
- 从查找表中删除数据元素。
查找表术语
静态查找表:在查找表中只做查找操作,而不改动表中数据元素,称此类查找表为静态查找表。
动态查找表:在查找表中做查找操作的同时进行插入数据或者删除数据的操作,称此类表为动态查找表。
关键字:关键字又细分为主关键字和次关键字。
主关键字:若某个关键字可以唯一地识别一个数据元素时,称这个关键字为主关键字,例如学生的学号就具有唯一性。
次关键字:像学生姓名、年龄这类的关键字,由于不具有唯一性,称为次关键字。
顺序查找算法
算法描述:
从表中的最后一个数据元素开始,逐个同记录的关键字做比较,如果匹配成功,则查找成功;如果直到表中第一个关键字查找完也没有成功匹配,则查找失败。
如下图所示:
下面我们用Python去实现顺序查找算法,代码如下:
def sequence_search(array, key):
"""
顺序查找算法
"""
for i in range(len(array)):
if array[i] == key:
return i
return False
array_0 = [23, 43, 12, 54, 65, 48]
print(sequence_search(array_0, 12))会把查找到的数字的索引值打印出来,输出结果如下:
折半查找算法
折半搜索也称二分搜索、对数搜索,是一种在有序数组中查找某一特定元素的搜索算法。
算法描述:
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
优缺点:
注意:折半查找算法只适用于有序表,无序表不可以用折半查找算法。
下面我们看一个具体的折半查找的例子,并分析具体过程:
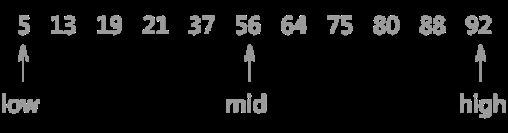
对{5,13,19,21,37,56,64,75,80,88,92}采用折半查找算法查找关键字为 21 的过程为:
1. 21 < 56 21一定存在于 low 和 mid 指向的区域中间,如下图:
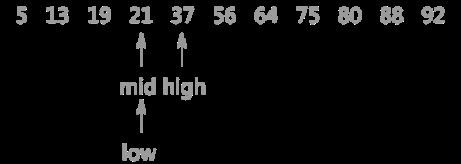
2. 更新 high 指针和 mid 指针的位置,令 high 指针移动到 mid 指针的左侧同时令 mid 重新指向 low 指针和 high 指针的中间位置。19 < 21,21肯定处于 mid 和 high 指向的区域中,如下图:
3.当第三次做判断时,发现 mid 就是关键字 21 ,查找结束,如下图:
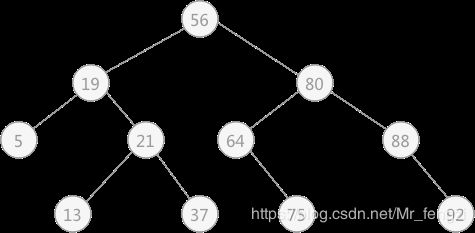
半查找的运行过程可以用二叉树来描述,这棵树通常称为“判定树”。
下面用Python实现折半查找算法,代码如下:
def halffind(nums, key, low, high):
"""
二分查找递归实现
"""
mid = (low + high) // 2
if key == nums[mid]:
return mid
if low > high:
return False
if key > nums[mid]:
return halffind(nums, key, mid + 1, high)
else:
return halffind(nums, key, low, mid - 1)对其进行测试,测试代码如下:
if __name__ == "__main__":
nums = [-789, -96, -53, 23, 52, 56, 520] # 测试案例
key = int(input("请输入要搜索的关键字:"))
print(halffind(nums, key, 0, len(nums)))测试结果如下: