coursera 吴恩达Neural Networks and Deep Learning 笔记
开始吴恩达深度学习辣!!
coursera DeepLearning
网易云课堂视频
Neural Networks and Deep Learning
Week 1
吹水
Week 2
2.1
讲一下深度学习的定义,机器学习里头X好像每行是一组数据,这里是每列是一组数据。
然后 n 就是特征数量啦,m 就是样本数量,有 m_train、m_test 等:

2.2
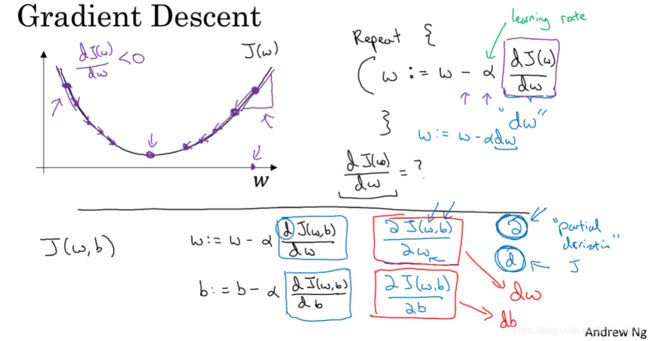
熟悉的 gradient descent ,这里 J ( w , b ) 对 w 求偏导的话,可以写成 dw ,对 b 求偏导同理。
然后如果是求偏导(有多个变量对某个变量求导数)的话,用花体的 d ,求导的话就是 d 。
然后这里不会像机器学习那样,把w和b融合到θ矩阵中,会分开w和b,w是列向量,b是个常数:

2.11
运用numpy的dot来进行点积(.dot 两个向量)和矩阵乘法(.dot 两个矩阵或一向量一矩阵),注:点积和矩阵乘法不同,点积:a.*b,矩阵乘法:a*b
如果调用库函数的话(不显式地用for循环),他会搞什么并行化运算,然后关乎SIMD啥的,然后GPU比CPU更擅长这个SIMD运算啥的(CPU也不赖),总之调库会比手写效率更高,而且又简洁。
放一些介绍的链接:
np.dot()使用方法
向量内积(点乘)和外积(叉乘)概念及几何意义
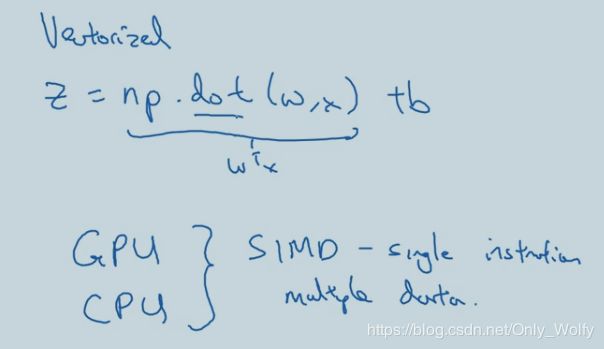
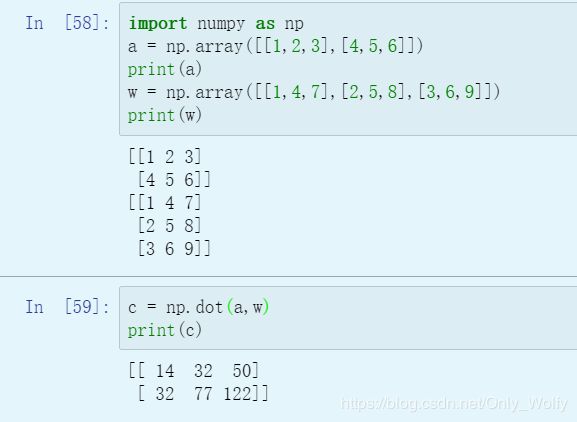
测试:
2.12
然后为了提高效率,尽量不显式地用for循环,还有很多函数可以调用,比如exp就是求一个矩阵是原矩阵所有元素作为e的指数的结果(大概意思 = = ):

V**2 就是矩阵每个元素平方一下:

2.13
这里b应该是 1 x m 维的,但是矩阵加上一个常数,就会每个元素都加上那个元素,相当于矩阵相加:
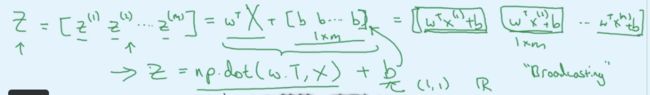
2.15 Broadcasting in Python
记了点Python语法
2.16 A note on python/numpy vectors
2.18 Explanation of logistic regression cost function (optional)
解释了下 logistic regression 的推导

用的是最大似然估计法,两边同时乘 log:

作业1 Python Basics with numpy (optional)
作业2 Logistic Regression with a Neural Network mindset
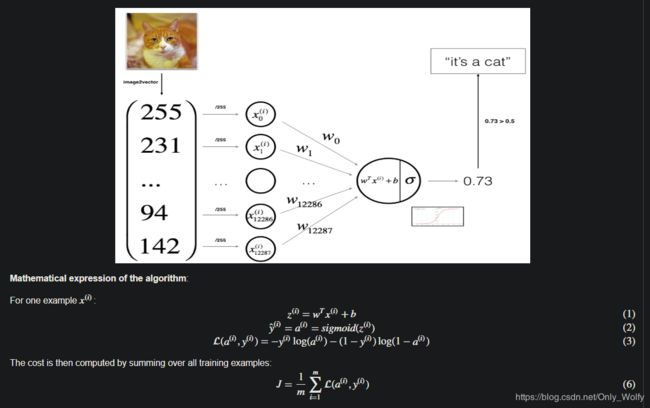
突然有了对L(a(i),y(i))函数的理解:(L:某个样本的误差,J:总体平均误差)
如果 y(注意和y_hat区分)是 1 的话,那么粗略地写就是:L = -ylog(a) = -log(a)
a越大,表示算法觉得越应该是1,log(a) 越大,然后 L 就越小,最后统计的是 J = 1/m sigma(L),本意就是要让 J 最小化,所以 L 越小越好,a 则越大越好
如果 y 是 0 的话,那么就是:L = -(1-y)log(1-a) = - log(1-a),a 越小,表示算法觉得越应该是0,1-a 越大,log(1-a) 越大,那么 L 越小,则 J 越小,符合让 J 最小化的本意。
过了。下面是遇到的问题:
- 有个函数有三个地方要填,但是我只填了一个就开始测试,然后编译不过,说w.T的T没有被定义,我:???,若不是旁边有人我就开骂了。然后找了一下错误找不到,把后面两个地方填了,编译就过了…
- 然后这里w,b一开始写了initialize_with_zeros(dim)。。鬼使神差,没有经过大脑写的,然后看了报错维数不对,就改成X_train.shape[1],发现还是不对改[0]才过。然后shape[0]是因为X.shape是(nx,m)nx是指一组样本有多少个元素,m是指有m组样本。所以是w是采用第0维的。

Week 3
3.4 Vectorizing across multiple examples

中括号里头是指第几层,小括号里头是指第几个样例(训练样本)。
以右下角A数组为例,第一列第一行为神经网络第一层的(第一个样例的)第一个点,第一列第二行为第一层第二个点,第二列第一行为第一层的(第二个样例的)第一个点。
PS: a 2 [ 1 ] a^{[1]}_{2} a2[1]表示第一层隐藏层中的第二个激活函数a(就是第一列圈圈的第二行的圈圈)
3.5 Explanation for Vectorized Implementation
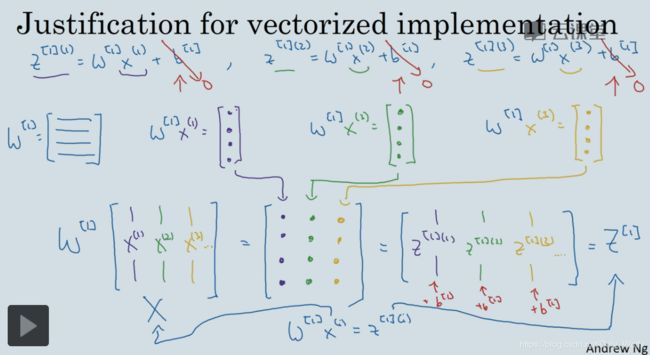

这节继续讲了如何使用向量化,可以看到w[1]x(1)、w[1]x(2)、w[1]x(3),其实就是不同样本下的第一层的值:z[1](1)、z[1](2)、z[1](3)… …然后为了方便运算所以摆成一列列。如果上图中,右上的代码和右下的代码作用是一样的。
最后注意从隐藏层第一层开始为[1],所以输入层的X矩阵,也可以用A[0]表示,Z是指输入的东西,可以看成球的左半部分,A是指输出的东西,可以看成球的右半边:
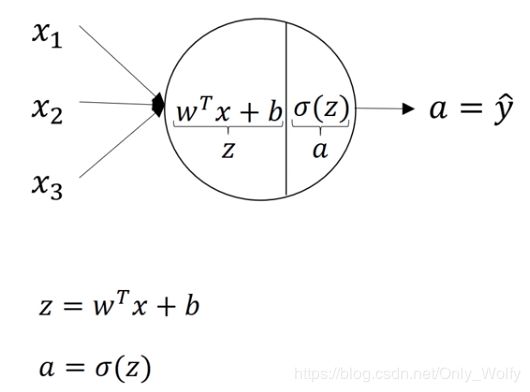
然后会了只有一个隐藏层的代码后,多个隐藏层也只是重复一下代码而已。
3.6 Why do you need non-linear activation functions?

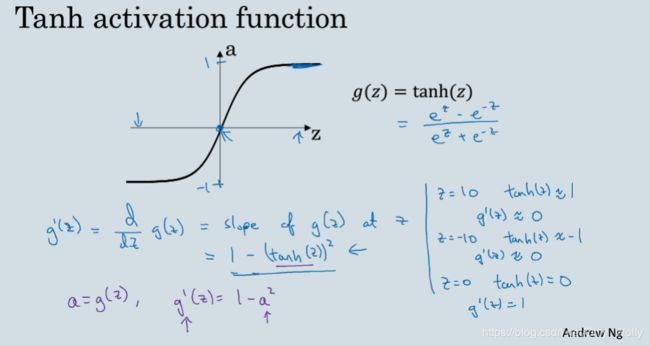
这节讲的激活函数,激活函数之前用的是sigmoid( a = 1 1 + e − z a=\frac{1}{1+e^{-z}} a=1+e−z1),但是在隐藏层用的是tan函数( a = t a n h ( z ) = e z − e − z e z + e − z a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} a=tanh(z)=ez+e−zez−e−z),除非是二元分类的输出层,都尽量不要采用sigmoid,因为:
此时函数的值 介于1和-1之间 因此隐藏层激活函数输出的平均值 会更加逼近于0 有时候当你 训练一个 学习算法的时候 你可能会中心化你的数据 并且使用tanh替代Sigmiod函数 以达到数据中心化的效果 数据中心化使数据的平均值 更加逼近零
吴恩达原话…大概这个意思吧
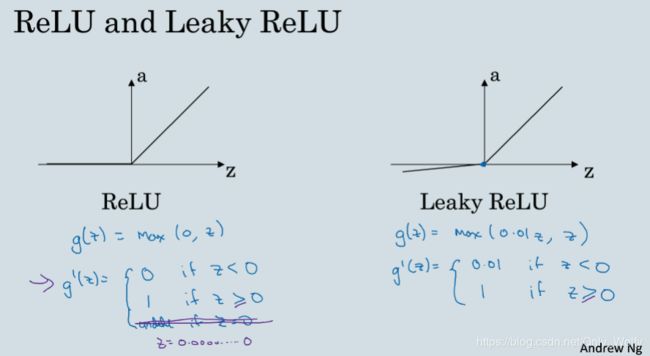
然后有个ReLU函数经常使用( a = m a x ( 0 , z ) a=max(0,z) a=max(0,z)),然后有个Leaky ReLU(带泄露ReLU, a = m a x ( 0.01 z , z ) a=max(0.01z,z) a=max(0.01z,z)),比较少人用0.01z是经验得出的,通常用ReLU。
这节课了解了热门和冷门的函数选择,需要根据自己的课题/目标来进行选择,可以在交叉数据集上多跑跑,看看哪个更好。
3.7 Why do you need non-linear activation functions?
建立激活函数是为了让神经网络实现一些有趣的功能。

如果没有激活函数的话(排除线性激活函数( g ( z ) = z g(z)=z g(z)=z)),那么就只是像右边的a一样,就是线性的堆砌,然后得出来也是线性的,没有什么实际意义,所以要弄非线性的激活函数。唯一需要用到线性激活函数( g ( z ) = z g(z)=z g(z)=z)的地方就是回归问题最后一层的输出(这里用ReLU也行)。
3.8 Derivatives of activation functions
介绍了激活函数的导数
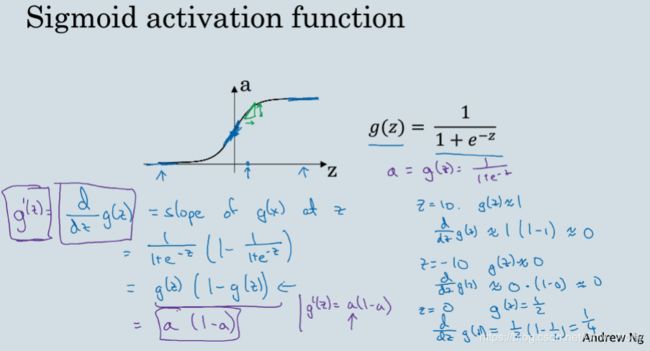
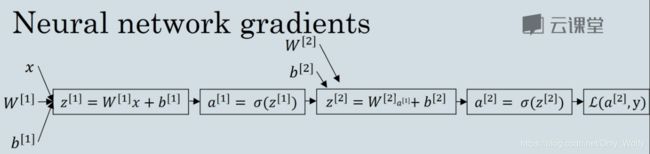
3.9 Gradient descent for Neural Networks
介绍了怎么执行梯度下降(具体推导下节讲)

3.10 Backpropagation intuition (optional)

采用链式法则推导,这里loss函数是交叉熵函数:
d a = d L ( a , y ) d a da = \frac{dL(a,y)}{da} da=dadL(a,y) ,具体怎么得出求导的,网上都有
d z = d L d a ⋅ d a d z = d a ⋅ σ ′ ( z ) dz = \frac{dL}{da}·\frac{da}{dz}=da· σ'(z) dz=dadL⋅dzda=da⋅σ′(z),这里用的是sigmoid函数(虽然之前说不再用了hh)
= d a ⋅ σ ( z ) ⋅ ( 1 − σ ( z ) ) = d a ⋅ a ⋅ ( 1 − a ) = a − y = da· σ(z)·(1-σ(z)) = da·a·(1-a)= a - y =da⋅σ(z)⋅(1−σ(z))=da⋅a⋅(1−a)=a−y
d w = d L d z ⋅ d z d w = d z ⋅ x dw = \frac{dL}{dz}·\frac{dz}{dw} = dz·x dw=dzdL⋅dwdz=dz⋅x
d b = d L d z ⋅ d z d b = d z db = \frac{dL}{dz}·\frac{dz}{db} = dz db=dzdL⋅dbdz=dz
下面是两层隐藏层的公式推导:
对于2层隐藏层的正向传播(左边是公式推导,右边是代码)

对于反向传播:(注意要除m,因为有m组)

最后点乘那里不是很懂为啥是点乘,ng说看维度,因为两个相同维度的东西相乘,所以是点乘。(嗯?????)后来再想想应该是里面的的数学意义吧,不过用维度也可以快速分辨出来(前提是式子列对了)
3.11 Random Initialization
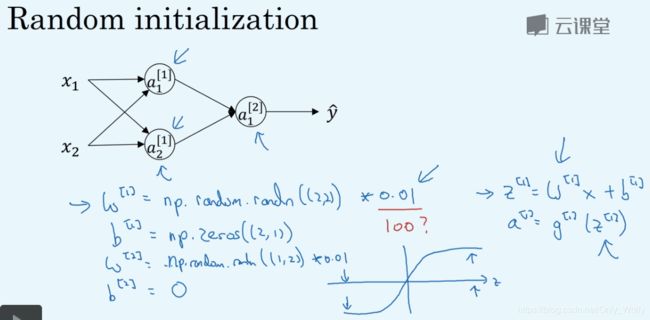
如果你把 w [ 1 ] w^{[1]} w[1]全初始化为0,那么这第一列的圈圈(隐藏单元)都是计算同一个东西,不管迭代多少次,但我们设立不同的隐藏单元是为了他们计算不同的函数。
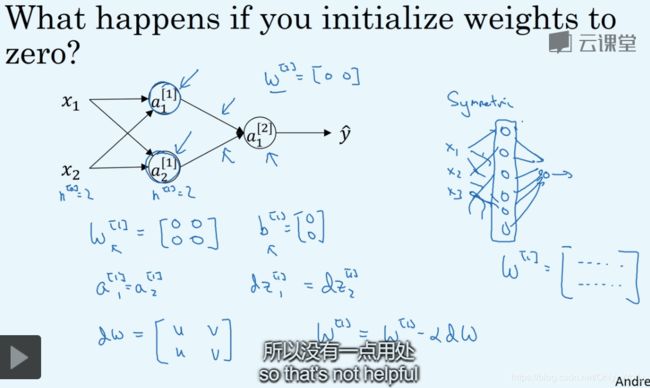
解决方案就是随机化数组,然后取0.01而不是100是因为如果激活函数是tanh或者sigmoid的话,那么导数会很小,不利于后续的梯度下降:
Week 4
4.1 Deep L-layer neural network
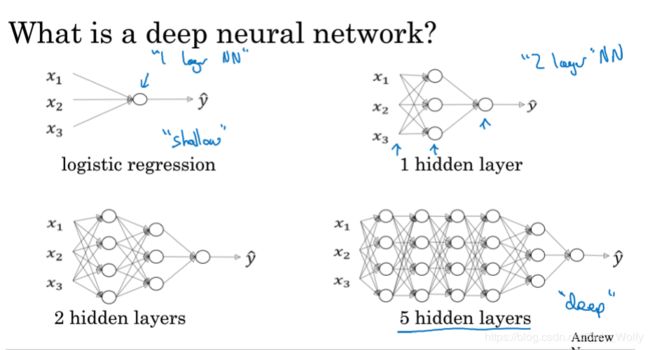
开始建造深度学习网络了,通常layer很多的才叫做deep,然后layer是隐藏层+输出层的数量
这里是一些符号的规范:
L是指layer, n l n^{l} nl就是第 l l l层的节点的数量, a l a^{l} al就是第 l l l层的激活函数,即 g [ l ] ( z [ l ] ) g^{[l]}(z^{[l]}) g[l](z[l]),所以 a [ 0 ] a^{[0]} a[0]也就是 X X X, a [ L ] a^{[L]} a[L]也就是 Y h a t Yhat Yhat,预测输出, W [ l ] W^{[l]} W[l]就是第 l l l层的 W W W, b [ l ] b^{[l]} b[l]就是第 l l l层的 b b b

4.2 Forward Propagation in a Deep Network
正向传递的式子。。没啥不一样,唯一注意的是用for来循环 l l l,因为没有更好的方法来加快每层的计算了
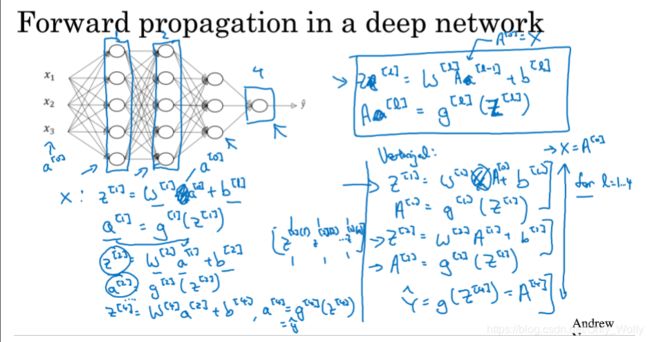
4.3 Getting your matrix dimensions right
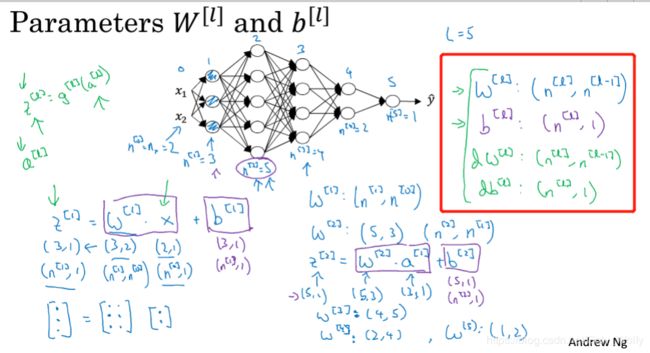
这节讲如何让你的矩阵维度正确:
- W 矩阵中,因为是 Z = WX + b,所以 W 的行数是 Z 的行数,列数是 X 的行数
然后 dW db 分别跟 W 和 b 一样大小 - 值得注意的是,Z、A、X 因为有了 m 个样本,所以列数要从1变为 m (1个样本的字母是z、a、x)

4.4 Why deep representations?
为什么要用深度学习?/ 为什么要用多一些隐藏层来做神经网络?
这里的解释是,以人脸识别为例,第一层用来探测边缘或者比较简单、粗糙的特征,下一层才探测一些五官,然后第三层才是人脸。这里有的觉得这就是大脑的运作,从粗糙的特征入手,再一步步细化。之前看了一些观点说大脑思考是仿照神经网络,但是人体是没有反向传播的,说明大脑没有用到的反向传播,但是仍达到了神经网络的效果。
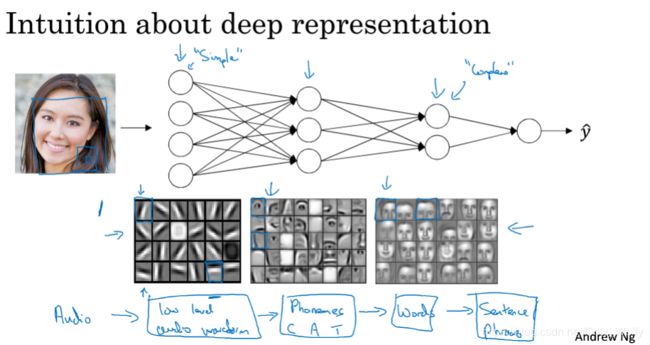
再来一个解释是,电路理论。如果有n个XOR,对于深层的,只要建一棵树,用logn的时间来完成就行。对于浅层的,比如1层隐藏层,就需要2^(n-1)个点(-1是因为n个数有n-1个圈圈(XOR)把它们连接起来),所以浅层要的时间会指数级增长。
最后,其实一开始解决问题的时候,推荐从logistic回归入手,然后效果不行再一步步增加层数。只有某些问题才需要弄很多层。
4.5 Building blocks of deep neural networks
下面讲解怎么构造deep的神经网络:
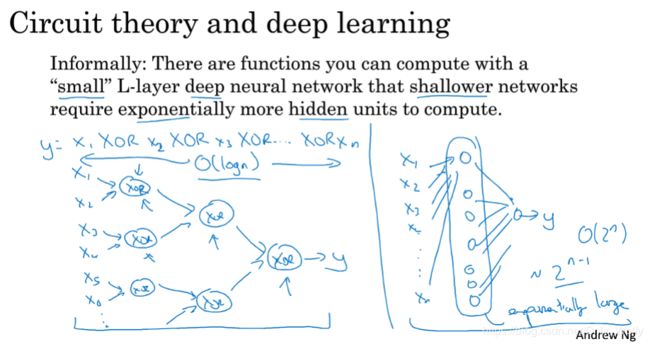
左边是forward和backward的参数,右边是大致的流程,蓝色(水平)箭头表示forward过程,红色反向箭头表示backward过程
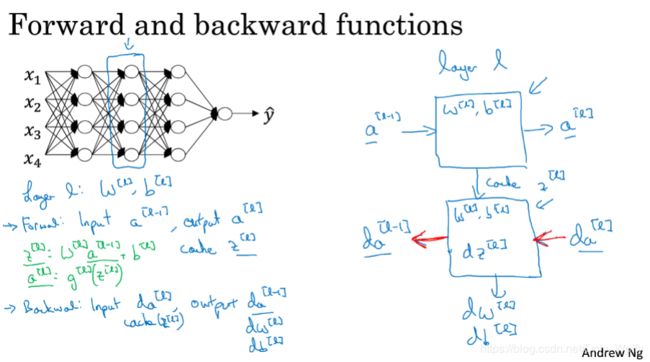
下面是更详细的神经网络forward和backward过程,绿色表示从头到尾的流程蓝色是forward,红色是backward,注意forward的时候会记录一个cache,方便backward的时候用到cache里面的参数。注意da[0]就不需要计算了。
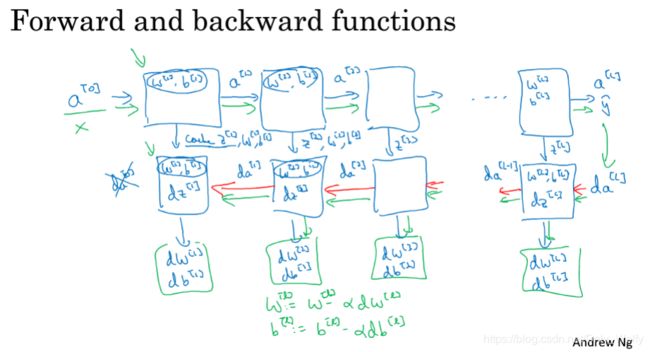
4.6 Forward and Backward Propagation
这节继续上节的内容,然后重点讲解bp的公式。这里 d a [ l − 1 ] da^{[l-1]} da[l−1]不知道怎么得来的。(其他不懂的可以看回3.10及其以下)
懂了,因为有个 z [ l ] = w [ l ] a [ l − 1 ] + b [ l ] z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]} z[l]=w[l]a[l−1]+b[l],所以 d L d a [ l − 1 ] = d L d z l ⋅ d z l d a [ l − 1 ] = d z l ⋅ w [ l ] \frac{dL}{da^{[l-1]}}=\frac{dL}{dz^l}·\frac{dz^l}{da^{[l-1]}}=dz^{l}·w^{[l]} da[l−1]dL=dzldL⋅da[l−1]dzl=dzl⋅w[l]
然后最后一行就是 d a [ l − 1 ] da^{[l-1]} da[l−1]代回第一行:

这个 d a [ l − 1 ] da^{[l-1]} da[l−1]代入 d z [ l ] dz^{[l]} dz[l]就得到绿色的式子,也就是下面3.10单层隐藏层的神经网络中的 d z [ 1 ] dz^{[1]} dz[1]式子:

总结:(又是这个图)记得字母要大写,因为有m组数据

最后再提一点:再强调一下 如果你觉得这些公式看起来有点抽象 不容易理解 我的建议是 认真完成作业 然后就会豁然开朗 但我不得不说 即便是现在 当我实现一个机器学习算法的时候 有时我也会惊讶 我的机器学习算法被证明有效 是因为机器学习的复杂度来源于数据而非一行行的代码 所以 有时候你会觉得 你写了几行代码 但不确定代码在干什么 最后它们竟然产生了神奇的结果 因为实际上大部分神奇的地方并不在你写的几行短短的代码中 可能并不是真的那么短 但不会是成千上万行 的代码而是碰巧输入了大量数据 即使我已经从事机器学习很多年了 有时候我依然感到意外 我的机器学习算法起效是因为算法的复杂度来源于数据 而不一定是你写的成千上万行的代码
神经网络的代码通常不会非常长,但却能够"work",其中的原因不一定是代码,而是大量的数据从量变引起了质变。
最后再梳理一下:首先得出 d a [ l ] da^{[l]} da[l](交叉熵情况下是 − y a + 1 − y 1 − a \frac{-y}{a}+\frac{1-y}{1-a} a−y+1−a1−y),然后得出了 d z [ l ] 、 d w [ l ] 、 d b [ l ] dz^{[l]}、dw^{[l]}、db^{[l]} dz[l]、dw[l]、db[l],然后再由 d z [ l ] dz^{[l]} dz[l]得出 d a [ l − 1 ] da^{[l-1]} da[l−1],因此就有了下一层的 d z [ l − 1 ] 、 d w [ l − 1 ] 、 d b [ l − 1 ] dz^{[l-1]}、dw^{[l-1]}、db^{[l-1]} dz[l−1]、dw[l−1]、db[l−1]……
(3.10的图:)

4.7 Parameters vs Hyperparameters
参数VS超参数:
什么是超参数?超参数就是可以控制参数的参数,比如迭代次数iter、学习率α、隐藏层的层数L、隐藏层隐藏单元的数量、对激活函数的选择,这些最终影响了 w l w^l wl和 b l b^l bl,还有以后的momentum(? 动量)、minibatch的大小,正则化参数等
超参数的选择:需要经过左边那个圈,来不断修改,比如右图,知道选择出满意的α,入手新项目时,需要用这个方法去找到最优的超参数,对于熟悉的项目,也应该隔一段时间检测一下,因为最优的超参数是会变的,因为CPU、GPU、网络和数据库在不断地更新:
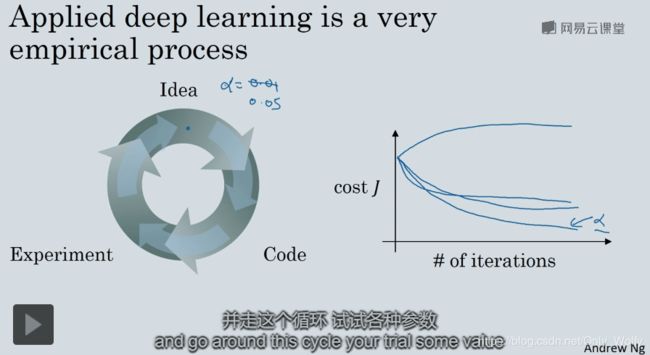
然后提到深度学习一个不太满意的地方:就是需要不断地尝试不同超参数的取值(然后在预留的交叉验证集或其他集合上进行评估,选取最优解)。在第二课中,我们会就如何系统地探索超参数空间提供一些建议。
4.8 What does this have to do with the brain?
深度学习与大脑之间有什么相似性呢?答:没有关系。
深度学习与大脑之间有什么相似性呢? 我总结之后 觉得它们之间的相似度并不高 我们先来看一下 为什么人们往往喜欢在 深度学习与人类大脑两者间进行比较 当你构建神经网络系统时 你会运用前向传播 和反向传播 由于我们很难去直观地解释 这些复杂的方程为什么能实现理想的效果 而将深度学习和人脑类比则 让这个过程过于简化却更便于说明 这种解释的简易程度让大众更轻易地 在各种媒介提及,使用或报道它 并且无疑地激发了公众的想象力 其实这之间确实有一些可对比的方向,比如说 逻辑回归单位和sigmoid激活函数 这是一个大脑神经元的图像 在这张生物意义上的神经元的图上,这个神经元 其实是你大脑的一个细胞, 它会接到其他神经元传来的电流信号 比如神经元x1,x2,x3,或者其他神经元a1,a2,a3 会做一个简单的阈值计算 然后如果这个神经元被触发 他会沿树突传送一股电流,在方向上一直传送 可能送至其他的神经元 所以存在一个简单地类比 这个类比体现在在独立的逻辑单位 神经网络中一个独立的神经元 和一个生物意义上的神经元(如右图所示)之间 但是我认为,直至今天 即便是神经学专家也几乎不清楚 哪怕是一个单一的神经元如何运作 一个神经元其实复杂得多 相比于我们用神经科学所够描述的 而它做的其中一部分工作有些像逻辑回归 但是还有很多单一神经元的工作 至今没有任何一个人,一个人类理解 比如 人脑中的神经元究竟如何学习依旧是个谜 而且至今我们不清楚到底人脑有没有一个类似 反向传播或者梯度下降的算法,亦或是 人脑运用了一个完全不同的学习原理 所以当我理解深度学习,我认为它非常善于学习 非常灵活的方程,非常复杂的方程, x到y的映射, 监督学习中输入到输出映射 而对于深度学习和大脑的类比,也许曾经是有用的 但是我认为,这个领域已经进步到了 可以打破这个类比的阶段 我倾向于不再运用这个类比 所以这就是我想说的神经网络和大脑的部分 我确实认为计算机视觉方向 相比于其他深度学习影响的学科,得到了更多的灵感 得到了更多的灵感 但是我个人比以前更少地使用人脑进行对比了 好,这就是这次课程的内容 你现在知道如何运用正向传导,反向传播和 梯度下降,以及深层的神经网络结构 希望你们能顺利做完课后练习 我期待在下节课程中和你们分享更多 GTC字幕组翻译
course1 结束啦!
