线性回归 李宏毅机器学习HW1
本文是李宏毅老师机器学习的第一次大作业,参考网上代码,写了一下自己的思路。
李宏毅 HM1:
要求:本次作業使用豐原站的觀測記錄,分成train set跟test set,train set是豐原站每個月的 前20天所有資料。test set則是從豐原站剩下的資料中取樣出來。 train.csv:每個月前20天的完整資料。 test_X.csv:從剩下的10天資料中取樣出連續的10小時為一筆,前九小時的所有觀測 數據當作feature,第十小時的PM2.5當作answer。一共取出240筆不重複的test data,請 根據feauure預測這240筆的PM2.5。

1review
首先回顾下线性回归的基本知识:
https://blog.csdn.net/ZHOUJIAN_TANK/article/details/83750105
关键的点:
step1:set a model ,很显然采用线性模型
step2:goodness of function 均方误差
step3:pick the best function Gradient descent
本次作业处理思路:
利用训练集对参数进行学习;对test data进行预测。
关键的地方(1)对train data 进行数据处理 ,数据如何存储和读取
(python 基础)
(2)向量的操作方法
下面补充一点向量的知识:

式中,N为训练集的样本数,为实际的值,x为输入值(可以为向量),w与b为训练参数(parament)。
2、分析:
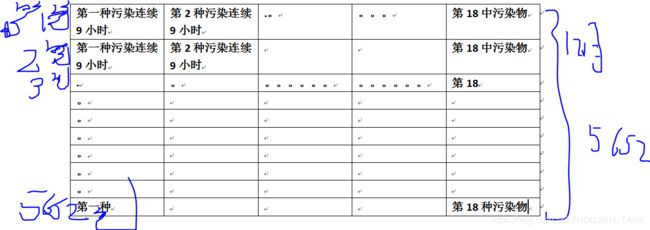
训练集中每个月20天,每天24个小时。根据前9个小时观测的所有数据(共18中污染物),
也就是18*9=162个feature输入来预测第10个小时的P,2.5值。由于数据的不连续性,
在连续取九个小时的过程中,每个月第20天的后9个小时是没有对应的实际对应的测量值的,
所以实际上每个月有 20*24-9=471笔连续9小时,也就是每个月有471笔训练数据,
一年就有 12*471=5652笔训练数据;每笔训练数据包含9个小时的18种污染物18*9=162,
也就是每笔数据有162个feature,需要162个参数外加一个bais需要163各参数。
function set 可设置为下:
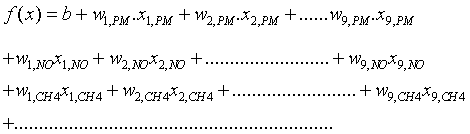
上式中,b为bias,w1,pm为PM的第一个小时观测值,w2,pm为PM的第二个小时观测值,
w3,pm为PM的第三个小时观测值。。。。。w9,PM为PM的第9个小时观测值weight值,。。。。。。。。。。。。以此类推,wi,cat 即为种类为cat的污染物第i小时的观测值的权重。。。。。。。。 18*9+1=163个paraments。
转换成向量的形式,即为:

其中 phi为训练数据集,5652笔训练数据,163个参数;第一个参数为bias,其余的为feature(污染物)。
3、代码分析
3.1对数据的处理
train数据的原始存储形式为:

处理原始的训练数据,方便对数据的使用。上图为一天的所有训练数据,为了方便操作,可以把18种污染物的所有数据,按照种类放在一个数组中data18, 每种污染物共202412=5670个数据也就是:原始表格转换为:

在数据转换为Data185670 基础上,再取的训练集与实际输出值。训练集为每个月所有可能连续9小时,共471种可能,每个训练里有 189=162个数据,怎么样取得162个数据?按照顺序 [第一种污染物连续9小时,第二种污染物连续9小时,第三种,。。。。。。。。第18种连续9小时]。得道转换后的训练集数据 X5652*162
代码如下:
################完成原始数据按按照每种污染物的类别进行存储##############
data = [] #data存什么?按类别存储 feature 共18种特征
for i in range(18):
data.append([])
n_row = 0
text = open('train.csv', 'r', encoding='big5')
row = csv.reader(text, delimiter=",")
print("type(text):", type(text))
print("type(row):", type(row))
for r in row: #遍历所有的行
# 0 cols
if n_row != 0:
for i in range(3, 27): #取所有的小时,注意数据在xls表格中的格式
if r[i] != "NR": #对 rainfall中的数据进行处理
data[(n_row - 1) % 18].append(float(r[i]))
else:
data[(n_row - 1) % 18].append(float(0)) #若不下雨则 rain 那一行加0
n_row = n_row + 1
text.close()
以上代码实现原始数据到 新的表格数据的存储转换。
# divide data
x = []
y = []
const_month = 12
a=len(data[0]) #每项指标所有的数据
src_data_in_month = int(len(data[0]) / const_month) # 5760/12
data_per_month = src_data_in_month - 9 # 471 每种特征数据每月存储的个数
# per month
a=0
for i in range(12):#12月
for j in range(data_per_month): #每月的特征数据
x.append([])
for t in range(18): #每种数据种数
for s in range(9):
x[471 * i + j].append(data[t][480 * i + j + s]) #每月的后9小时不参与预测
y.append(data[9][480 * i + j + 9]) # s=9 ;y里存储的是 PM2.5,每月第一天的前九个数据不参与预测
print("after append,x[0]:", x[0])
print("len(x):", len(x))
x = np.array(x)
y = np.array(y)
print("len(x):", len(x))
x = np.concatenate((np.ones((x.shape[0], 1)), x), axis=1) #add bias 在原来x的基础上在第一列之前添加一列每个元素值为1
3.2训练数据
w = np.zeros(len(x[0])) #参数的初始值 设置为 0,共163个参数
print("len(x[0]):", len(x[0]))
l_rate = 10 #learning-rate
repeat = 10000 #迭代次数
x_t = x.transpose()
s_gra = np.zeros(len(x[0])) #grad
for i in range(repeat): #迭代次数
hypo = np.dot(x, w) #(5652,1),这一步得到是所有训练集组成的一个预测值组成的 矩阵
loss = hypo - y #(5652,1) 预测数值-真实数值,
cost = np.sum(loss ** 2) / len(x) #loss 均方误差和
cost_a = math.sqrt(cost) #这句话和上面三句话用来求LOSS function均方根,代表的都是数据拟合的好坏
#梯度下降
gra = np.dot(x_t, loss) #这里不懂,应该是矩阵的导数
s_gra += gra ** 2 #sum_grad
ada = np.sqrt(s_gra)
w = w - l_rate * gra / ada #完成参数的一次迭代更新,具体参考上面的公式
print('iteration:%d | Cost: %f ' % (i, cost_a))
#save model
np.save('model.npy', w)
#read model
w2 = np.load('model.npy')
#完成迭代更新,得到训练的参数w。
3.3测试数据
# test
test_x = []
n_row = 0
text = open('test.csv', "r")
row = csv.reader(text, delimiter=",")
for r in row: #读取测试集的数据存储到test_x[]中
if n_row % 18 == 0: #按指每次的第一行,也就是18的倍数行
test_x.append([])
for i in range(2, 11):
test_x[n_row // 18].append(float(r[i]))
else:
for i in range(2, 11):
if r[i] != "NR":
test_x[n_row // 18].append(float(r[i]))
else:
test_x[n_row // 18].append(0)
n_row = n_row + 1
text.close()
test_x = np.array(test_x)
test_x = np.concatenate((np.ones((test_x.shape[0], 1)), test_x), axis=1)
以上实现读取测试集原始数据,完成数据的转换。
ans = []
yy=[]
for i in range(len(test_x)):
ans.append(["id_" + str(i)])
a = np.dot(w, test_x[i])
ans[i].append(a) #得到预测值
yy.append(a)
#以上得到最终的预测值。
**
代码附录:
**
#_author_:'alex zhou'
# Time: 2018/10/18 0018
import csv #读写CSV数据
import numpy as np
import math
import matplotlib.pyplot as plt
# parse data
# initial
data = [] #data存什么?按类别存储 feature 共18种特征
for i in range(18):
data.append([])
n_row = 0
# print("data:",data)
# print("type(data):",type(data))
text = open('train.csv', 'r', encoding='big5')
row = csv.reader(text, delimiter=",")
print("type(text):", type(text))
print("type(row):", type(row))
for r in row:
# 0 cols
if n_row != 0:
for i in range(3, 27): #取所有的小时
if r[i] != "NR": #对 rainfall中的数据进行处理
data[(n_row - 1) % 18].append(float(r[i]))
else:
data[(n_row - 1) % 18].append(float(0)) #若不下雨则 rain 那一行加0
n_row = n_row + 1
text.close()
# print("data[0]:", data[0][:12])
# print("data[1]:", data[1][:12])
# with open('data.csv','w') as myfile:
# mywriter=csv.writer(myfile)
# mywriter.writerows(data)
# divide data
x = []
y = []
const_month = 12
a=len(data[0]) #每项指标所有的数据
src_data_in_month = int(len(data[0]) / const_month) # 5760/12
data_per_month = src_data_in_month - 9 # 471 每种特征数据每月存储的个数
# per month
a=0
for i in range(12):#12月
for j in range(data_per_month): #每月的特征数据
x.append([])
for t in range(18): #每种数据种数
for s in range(9):
x[471 * i + j].append(data[t][480 * i + j + s])
y.append(data[9][480 * i + j + 9]) # s=9 ;y里存储的是 PM2.5,第一天的前九个数据不参与预测
print("after append,x[0]:", x[0])
print("len(x):", len(x))
x = np.array(x)
y = np.array(y)
print("len(x):", len(x))
x = np.concatenate((np.ones((x.shape[0], 1)), x), axis=1) #add bias 在原来x的基础上在第一列之前添加一列每个元素值为1 #拼接 x.shape[0]为5652 shape函数是numpy.core.fromnumeric中的函数,它的功能是查看矩阵或者数组的维数。
# with open('123.csv','w') as myfile:
# mywriter=csv.writer(myfile)
# mywriter.writerows(x)
print(len(x[0])) #为163
w2 = np.matmul(np.matmul(inv(np.matmul(x.transpose(), x)), x.transpose()), y) #matual矩阵相乘
################################################
# train
w = np.zeros(len(x[0]))
print("len(x[0]):", len(x[0]))
l_rate = 10 #learning-rate
repeat = 10000 #迭代次数
# print("w[0]:",w[0][:10])
# print("w[1]:",w[1][:10])
x_t = x.transpose()
s_gra = np.zeros(len(x[0]))
for i in range(repeat): #迭代次数
hypo = np.dot(x, w) #(5652,1)
loss = hypo - y #(5652,1) 预测数值-真实数值
cost = np.sum(loss ** 2) / len(x) #loss
cost_a = math.sqrt(cost) #这句话和上面三句话用来求LOSS function均方根,代表的都是数据拟合的好坏
#梯度下降
gra = np.dot(x_t, loss) #这里不懂,应该是矩阵的导数
s_gra += gra ** 2 #sum_grad
ada = np.sqrt(s_gra)
w = w - l_rate * gra / ada
print('iteration:%d | Cost: %f ' % (i, cost_a))
#save model
np.save('model.npy', w)
#read model
w2 = np.load('model.npy')
#######################################################
# test
test_x = []
n_row = 0
text = open('test.csv', "r")
row = csv.reader(text, delimiter=",")
for r in row: #读取测试集的数据存储到test_x[]中
if n_row % 18 == 0: #按指每次的第一行,也就是18的倍数行
test_x.append([])
for i in range(2, 11):
test_x[n_row // 18].append(float(r[i]))
else:
for i in range(2, 11):
if r[i] != "NR":
test_x[n_row // 18].append(float(r[i]))
else:
test_x[n_row // 18].append(0)
n_row = n_row + 1
text.close()
test_x = np.array(test_x)
test_x = np.concatenate((np.ones((test_x.shape[0], 1)), test_x), axis=1)
#######################################################3
# test
ans = []
yy=[]
for i in range(len(test_x)):
ans.append(["id_" + str(i)])
a = np.dot(w, test_x[i])
ans[i].append(a) #得到预测值
yy.append(a)
#############
## 这一部分是把得出的 pm2.5 的数值写入 predict.csv文件
filename = "predict.csv"
text = open(filename, "w+")
s = csv.writer(text, delimiter=',', lineterminator='\n')
s.writerow(["id", "value"])
for i in range(len(ans)):
s.writerow(ans[i])
text.close()
#plot
row_n = 0
y = []
text = open('ans.csv', 'r', encoding = 'big5')
row = csv.reader(text, delimiter = ',') # 此处 delimiter = ',' 有没有无所谓,这句话用来当一行中用 ','时分割句子的
for r in row:
if row_n != 0:
y.append(r[1])
row_n = row_n + 1
text.close()
plt.figure(figsize = (13, 7))
plt.plot(np.arange(0, 240, 1), yy, 'r', label = 'prediction pm2.5')
plt.plot(np.arange(0, 240, 1), y, 'b', label = 'ans pm2.5')
plt.legend()
plt.show()