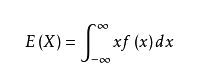小结:
(泛义的)高数很重要,高数是一切经济学和数据分析的基础。未来大数据也会用到的。含义和公式不难,比较难的是如何应用。python比较适合快速处理大量数据,excel适合边看图表边计算,顺便给销售/财务/so on做一些自动模板。
- 数学含义与公式
(1) 加权平均值
(2) 相关系数
(3) 方差
(4) 协方差
(5) 数学期望值 E - Python3.6 实现
2.1. python 计算加权平均数
2.2 python 计算分组加权平均数
2.3 相关系数 - 拓展 excel 计算
1. 数学含义与公式
(1) 加权平均值即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。
(2) 相关系数
简单相关系数:又叫相关系数或线性相关系数,一般用字母r 表示,用来度量两个变量间的线性关系。
Cov(X,Y)为X与Y的协方差,Var[X]为X的方差,Var[Y]为Y的方差
(3) 方差
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
(4) 协方差
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为E(X) = μ 与 E(Y) = ν 的两个实数随机变量X与Y之间的协方差定义
分别为m与n个标量元素的列向量随机变量X与Y,二者对应的期望值分别为μ与ν,这两个变量之间的协方差定义为m×n矩阵。
(5) 数学期望值 E
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
设连续性随机变量X的概率密度函数为f(x),若积分绝对收敛, 数学期望计算如下
(5) 标准普尔500指数
标准普尔500指数英文简写为S&P 500 Index,是记录美国500家上市公司的一个股票指数。
标准·普尔500指数具有采样面广、代表性强、精确度高、连续性好等特点,被普遍认为是一种理想的股票指数期货合约的标的。
标准普尔的实力在于创建独立的基准。通过标准普尔的信用评级,他们以客观分析和独到见解真实反映政府、公司及其它机构的偿债能力和偿债意愿,并因此获得全球投资者的广泛关注。
2. Python3.6 实现
数据集地址
https://github.com/kojoidrissa/pydata-book/tree/master/ch09
2.1. python 计算加权平均数
In [208]: test = DataFrame({'data':np.random.randn(10),
...: 'weights':np.random.rand(10)})
...:
In [209]:
In [209]: test
Out[209]:
data weights
0 1.617083 0.498272
1 -0.298687 0.431866
2 -0.587101 0.931359
3 1.215299 0.062998
4 -0.710441 0.559426
5 -0.692910 0.622395
6 -0.065183 0.732230
7 1.041070 0.750380
8 0.644148 0.065128
9 0.844851 0.144296
In [210]: np.average(test['data'],weights=test['weights'])
Out[210]: 0.057340757362767489
2.2 python 计算分组加权平均数
In [194]: list = ['a']* 4 + ['b'] * 6
In [195]: list
Out[195]: ['a', 'a', 'a', 'a', 'b', 'b', 'b', 'b', 'b', 'b']
In [196]: df = DataFrame({'category' : list,
...: 'data': np.random.randn(10),
...: 'weights': np.random.rand(10)})
In [197]: df
Out[197]:
category data weights
0 a -0.223955 0.017115
1 a 0.627805 0.204209
2 a -0.895798 0.904739
3 a 1.254223 0.551053
4 b -1.024985 0.904737
5 b -0.027101 0.263672
6 b -2.501462 0.364224
7 b 0.008169 0.805655
8 b 1.603461 0.630892
9 b -1.099844 0.596945
In [198]: grouped = df.groupby('category')
In [199]: get_wavg = lambda g : np.average(g['data'],weights=g['weights'])
In [200]: grouped.apply(get_wavg)
Out[200]:
category
a 0.003011
b -0.416120
dtype: float64
2.3 相关系数
话说这个在coursera上也有说到...excel上也可以算。感觉难的不是代码,是概念和用法。
注意底数是什么。
# 读取日收益率
In [213]: close_px = pd.read_csv('ch09/stock_px.csv',parse_dates=True,index_col
...: =0)
In [214]: close_px
Out[214]:
AAPL MSFT XOM SPX
2003-01-02 7.40 21.11 29.22 909.03
2003-01-03 7.45 21.14 29.24 908.59
2003-01-06 7.45 21.52 29.96 929.01
2003-01-07 7.43 21.93 28.95 922.93
2003-01-08 7.28 21.31 28.83 909.93
2003-01-09 7.34 21.93 29.44 927.57
2003-01-10 7.36 21.97 29.03 927.57
2003-01-13 7.32 22.16 28.91 926.26
2003-01-14 7.30 22.39 29.17 931.66
2003-01-15 7.22 22.11 28.77 918.22
2003-01-16 7.31 21.75 28.90 914.60
2003-01-17 7.05 20.22 28.60 901.78
2003-01-21 7.01 20.17 27.94 887.62
2003-01-22 6.94 20.04 27.58 878.36
2003-01-23 7.09 20.54 27.52 887.34
2003-01-24 6.90 19.59 26.93 861.40
2003-01-27 7.07 19.32 26.21 847.48
2003-01-28 7.29 19.18 26.90 858.54
2003-01-29 7.47 19.61 27.88 864.36
2003-01-30 7.16 18.95 27.37 844.61
2003-01-31 7.18 18.65 28.13 855.70
2003-02-03 7.33 19.08 28.52 860.32
2003-02-04 7.30 18.59 28.52 848.20
2003-02-05 7.22 18.45 28.11 843.59
2003-02-06 7.22 18.63 27.87 838.15
2003-02-07 7.07 18.30 27.66 829.69
2003-02-10 7.18 18.62 27.87 835.97
2003-02-11 7.18 18.25 27.67 829.20
2003-02-12 7.20 18.25 27.12 818.68
2003-02-13 7.27 18.46 27.47 817.37
... ... ... ... ...
2011-09-02 374.05 25.80 72.14 1173.97
2011-09-06 379.74 25.51 71.15 1165.24
2011-09-07 383.93 26.00 73.65 1198.62
2011-09-08 384.14 26.22 72.82 1185.90
2011-09-09 377.48 25.74 71.01 1154.23
2011-09-12 379.94 25.89 71.84 1162.27
2011-09-13 384.62 26.04 71.65 1172.87
2011-09-14 389.30 26.50 72.64 1188.68
2011-09-15 392.96 26.99 74.01 1209.11
2011-09-16 400.50 27.12 74.55 1216.01
2011-09-19 411.63 27.21 73.70 1204.09
2011-09-20 413.45 26.98 74.01 1202.09
2011-09-21 412.14 25.99 71.97 1166.76
2011-09-22 401.82 25.06 69.24 1129.56
2011-09-23 404.30 25.06 69.31 1136.43
2011-09-26 403.17 25.44 71.72 1162.95
2011-09-27 399.26 25.67 72.91 1175.38
2011-09-28 397.01 25.58 72.07 1151.06
2011-09-29 390.57 25.45 73.88 1160.40
2011-09-30 381.32 24.89 72.63 1131.42
2011-10-03 374.60 24.53 71.15 1099.23
2011-10-04 372.50 25.34 72.83 1123.95
2011-10-05 378.25 25.89 73.95 1144.03
2011-10-06 377.37 26.34 73.89 1164.97
2011-10-07 369.80 26.25 73.56 1155.46
2011-10-10 388.81 26.94 76.28 1194.89
2011-10-11 400.29 27.00 76.27 1195.54
2011-10-12 402.19 26.96 77.16 1207.25
2011-10-13 408.43 27.18 76.37 1203.66
2011-10-14 422.00 27.27 78.11 1224.58
[2214 rows x 4 columns]
# 丢弃NAN项
In [215]: rets = close_px.pct_change().dropna()
# 计算相关系数的lambda函数(主要用于分组)
In [216]: spx_corr = lambda x : x.corrwith(x['SPX'])
# 按年份分组
In [217]: by_year = rets.groupby(lambda x:x.year)
# 按年份计算各股票与SPX的相关系数
In [218]: by_year.apply(spx_corr)
Out[218]:
AAPL MSFT XOM SPX
2003 0.541124 0.745174 0.661265 1.0
2004 0.374283 0.588531 0.557742 1.0
2005 0.467540 0.562374 0.631010 1.0
2006 0.428267 0.406126 0.518514 1.0
2007 0.508118 0.658770 0.786264 1.0
2008 0.681434 0.804626 0.828303 1.0
2009 0.707103 0.654902 0.797921 1.0
2010 0.710105 0.730118 0.839057 1.0
2011 0.691931 0.800996 0.859975 1.0
# 任意两股票的相关系数如下计算
In [219]: by_year.apply( lambda g : g['AAPL'].corr(g['MSFT']))
Out[219]:
2003 0.480868
2004 0.259024
2005 0.300093
2006 0.161735
2007 0.417738
2008 0.611901
2009 0.432738
2010 0.571946
2011 0.581987
dtype: float64
3. 拓展 excel 计算
python比较快..但是excel也可以算,如果是一边做图表一边算(或者做模板),可能excel会方便点。自动化其实还可以写VBA。
用基本的Excel函数计算商业指标--杜克大学
https://www.jianshu.com/p/20a289309f21
2018.8.24
含义来自谷歌和百度的信息(高数书不在手边..)
python 代码来自 《用python进行数据分析》
Excel 来自 coursera 上的公开课