关于ID3，C4.5，CART三种决策树算法及其所用分割依据（信息增益，信息增益率，基尼不纯度）的见解

阅读本篇博客，假定你有一定高等数学，概率论（贝叶斯定理）基础.

在开始之前先推荐一个常用的机器学习数据集网站：

加州大学欧文分校UCI（University of California，Irvine）的机器学习数据集库：UCI machine learning repos

这可能是世界上最出名的机器学习数据集库.对于每份数据，都有相应的索引文件，和对数据的解释文件，包含是否有缺失数据等关键信息.

决策树（decision tree）：维基的解释是：A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements.

通俗点说，决策树就是决策的流程图，对主要的特征值进行分类，最终得到分类标签（叶子节点）.

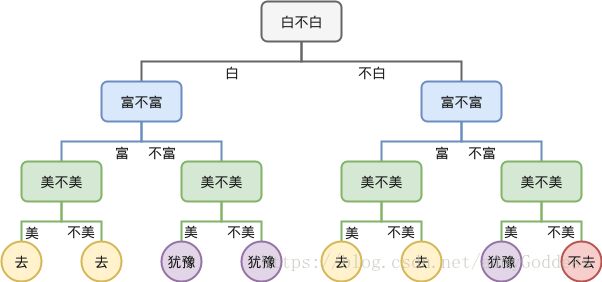
下面是一棵关于是否去相亲的决策树：

 

ID3决策树：ID3可能是目前常用的最简单的决策树算法，他有几个关键的特点，只能处理离散数据，不能用于处理连续值的特征值，其次，他对于缺失数据敏感，必须先手工处理缺失数据才能运用，最后他构造决策树的过程中分割数据值的根据是信息增益，即 info_gain = before_split_entorpy - after_split_entropy. Entropy.  即信息的量度香农熵. ID3会倾向于选择值多的特征来进行分割，ID3构造的决策树通常会有过度拟合（overfitting）的问题，即枝叶过多.

 

C4.5决策树：C4.5 algorithm是对ID3的改进，C4.5可以处理连续值，C4.5在构造决策树后会有pruning trees after creation（剪枝）的步骤.

C4.5不使用信息增益作为分割数据集的根据，改为使用信息增益率.

 

CART决策树（Classification And Regression Tree）：CART algorithm既可以用于创建分类树，也可以用于创建回归树.

他采用二分（binary split）来处理数据集，即每次都将数据集分割为两部分，依据是GIni Impurity（基尼不纯度）

下面详细解释三种分割依据：

 

1. 基尼不纯度

基尼不纯度可能是这三种分割依据里最容易理解的.基尼不纯度,是指将来自集合中的某种结果随机应用在集合中，某一数据项的预期误差率. 通俗来说。基尼不纯度代表了随机从数据集中抽取两个样本，其分类不一致的概率、

下面用贝叶斯定理和全概率公式推导基尼不纯度的计算公式：

假设数据集足够大.

基尼不纯度=IG（f）

p（c）= 随机抽取两个样本，其分类不一致

IG（f）=P（c）

p（i）表示i分类在数据集中所占的比例

V=（V1，V2，V3..Vn） Vn表示第一个随机抽到分类为n的样本

则v为全状态空间

p（c）=p（cv）=p（c | v）p（v）

由全概率公式：

p（c | v）p（v）= （c | Vi）p（Vi）=  p（i） * (1-p（i）)= p(i) - p(i)²=1 - p（i）²

 基尼不纯度=IG（f）= 1 - p（i）²

基尼不纯度越大，表示数据集越混乱，越小，表示数据集越纯。极端条件下，数据集中只有一个类别，IG（f）= 0，当有N种类别且每种均匀时，IG（f）=1 - . 也就是 离散型均匀随机变量的不纯度最大，IG（f）【0,1）左闭右开区间.

 

2.信息增益

首先是信息熵（Entropy）：信息熵是用来量化信息的工具

对于整个系统而言，熵是整个系统的平均消息量，即整个数据集的混乱程度，可以理解为为了了解一件事，需要的信息量，对于数据集：

此时的单位是bit（以2为底数）

对于一个离散型随机变量，当它是均匀分布时，其熵最大，通俗理解就是，假定一个随机变量，且概率都是25%.采用决策树类似的二元问题，从尽可能用少量的问题找出答案的角度，由于每个取值的可能性相当，所以我们相当于没有任何可用的额外信息，只能瞎猜，第一个问题是答案为a吗，第二个是答案为b吗，直至找出答案为止。

此时我们所需问题的数量的数学期望值为

但是当p（b）=85%，p（a）=p（c）=p（d）=5%时，第一个问题肯定是答案为b吗，此时我们有85%的几率只需提问一个问题就能得到答案，这时所需问题数量的数学期望值为：

这就是所谓当随机变量均匀分布时，知晓答案所需的信息量最大.  N为分类的数量

下面用拉格朗日乘子法证明这个结论：

 

是一个下凸函数（下凸函数的证明，有兴趣的可以自己尝试一下），拉格朗日乘子法是用来求约束条件下函数的极值，定义：

其中f为原函数，g为约束条件，是各变量的线性组合，它只在原函数为凸函数时保证正确。

对于熵函数：

约束条

将约束条件引入熵函数：

 

分别对p1，p2,...pn和求偏导，并令其等于0，有：

....

联立可得

证毕

将信息增益作为判断依据有个非常大的缺点，该算法倾向于选择值的种类比较多的特征值进行划分，为什么呢，因为其划分后的信息熵是各自数据集的熵的数学期望值，同一个数据集，将其划分的种类越多，自数据集内部的数据项就越少，也就越不混乱.这往往使得构造的整棵树非常庞大，C4.5正是改进了这一算法，使用信息增益率.

3.信息增益率：

信息增益率同样需要算信息增益，但它还需要计算分裂信息度量SplitInformation(S，A)。分裂信息度量其实非常简单，将分割后的数据集仍作为一个整体，此时被分割为同一个子集的数据将被视为同类.计算他的信息熵.例如一个数据集，他被分割成2部分，每部分的占比都是50%，此时它的SplitInformation(S，A)==1

信息增益率定义为：

前面说过，取值越多，越均匀的随机变量的熵越大，将其作为分母，可以抵消一部分信息增益对于多值特征的倾向.

 

下一篇博客，我将使用python分别实现这三种决策树算法，并详细比较其性能（包括使用范围，构造树的时间，分类器的准确性等）