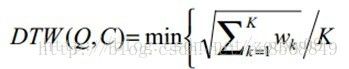DTW的基本原理及其C语言实现
DTW的原理 可以参考这篇文章,写的很详细。
http://www.cnphp6.com/archives/60574
这篇文章是没有代码的,我用C语言实现了文章里的描述的DTW方法,为了方便对照原理和代码,我将文章粘贴过来,然后附上C代码。
原理
在大部分的学科中,时间序列是数据的一种常见表示形式。对于时间序列处理来说,一个普遍的任务就是比较两个序列的相似性。
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。因为语音信号具有相当大的随机性,即使同一个人 在不同时刻发同一个音,也不可能具有完全的时间长度。而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“A”这个音拖得很长,或者把“i”发的很短。在这些复杂情况下,使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离(或者相似性)。
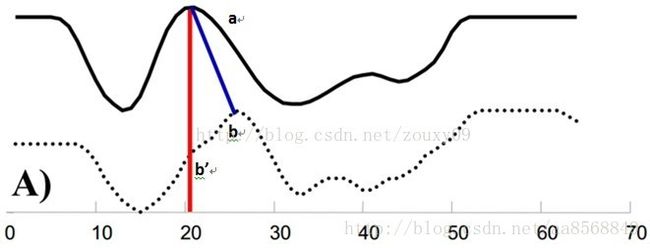
例如图A所示,实线和虚线分别是同一个词“pen”的两个语音波形(在y轴上拉开了,以便观察)。可以看到他们整体上的波形形状很相似,但在时间轴上却是不对齐的。例如在第20个时间点的时候,实线波形的a点会对应于虚线波形的b’点,这样传统的通过比较距离来计算相似性很明显不靠谱。因为很明显,实线的a点对应虚线的b点才是正确的。而在图B中,DTW就可以通过找到这两个波形对齐的点,这样计算它们的距离才是正确的。
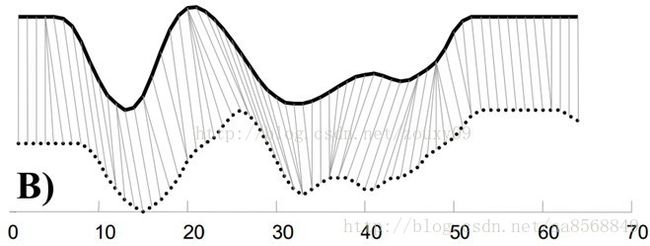
也就是说,大部分情况下,两个序列整体上具有非常相似的形状,但是这些形状在x轴上并不是对齐的。所以我们在比较他们的相似度之前,需要将其中一个(或者两个)序列在时间轴下warping扭曲,以达到更好的对齐。而DTW就是实现这种warping扭曲的一种有效方法。DTW通过把时间序列进行延伸和缩短,来计算两个时间序列性之间的相似性。
那如果才知道两个波形是对齐了呢?也就是说怎么样的warping才是正确的?直观上理解,当然是warping一个序列后可以与另一个序列重合recover。这个时候两个序列中所有对应点的距离之和是最小的。所以从直观上理解,warping的正确性一般指“feature to feature”的对齐。
注明:由B)图可以看出,模板序列中的一个点(这里的点可能是单个数值或是一个向量)可能对应测试序列中的好几个点(也有可能反过来,模板中的好几个点对应测试中的一个点),这正好反映了特征可能的延迟性。比如同一个音素,有的时候发得快,有的时候发的慢。这两种情况进行匹配时,你要把发得快的那个点完全匹配到发的慢的那几个点上。
2 原理
动态时间规整DTW是一个典型的优化问题,它用满足一定条件的的时间规整函数W(n)描述测试模板和参考模板的时间对应关系,求解两模板匹配时累计距离最小所对应的规整函数。
假设我们有两个时间序列Q和C,他们的长度分别是n和m:(实际语音匹配运用中,一个序列为参考模板,一个序列为测试模板,序列中的每个点的值为语音序列中每一帧的特征值。例如语音序列Q共有n帧,第i帧的特征值(一个数或者一个向量)是qi。至于取什么特征,在这里不影响DTW的讨论。我们需要的是匹配这两个语音序列的相似性,以达到识别我们的测试语音是哪个词)
Q = q1, q2,…,qi,…, qn ;
C = c1, c2,…, cj,…, cm ;
如果n=m,那么就用不着折腾了,直接计算两个序列的距离就好了。但如果n不等于m我 们就需要对齐。最简单的对齐方式就是线性缩放了。把短的序列线性放大到和长序列一样的长度再比较,或者把长的线性缩短到和短序列一样的长度再比较。但是这 样的计算没有考虑到语音中各个段在不同情况下的持续时间会产生或长或短的变化,因此识别效果不可能最佳。因此更多的是采用动态规划(dynamic programming)的方法。
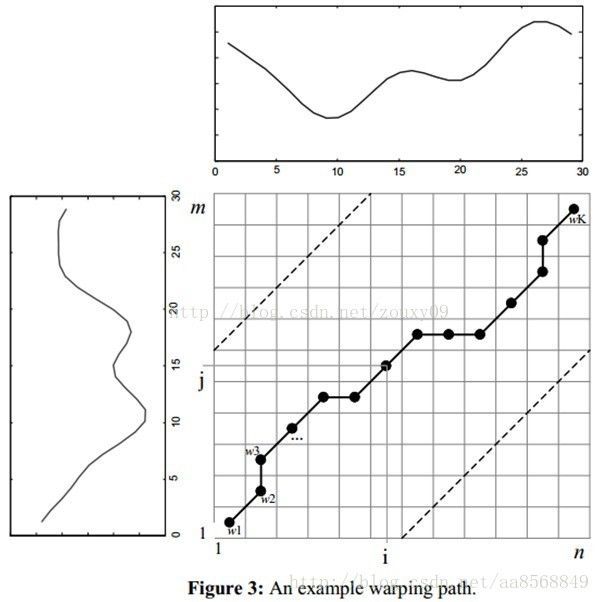
为了对齐这两个序列,我们需要构造一个n x m的矩阵网格,矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj)(也就是序列Q的每一个点和C的每一个点之间的相似度,距离越小则相似度越高。这里先不管顺序),一般采用欧式距离,d(qi, cj)= (qi-cj)2(也可以理解为失真度)。每一个矩阵元素(i, j)表示点qi和cj的对齐。DP算法可以归结为寻找一条通过此网格中若干格点的路径,路径通过的格点即为两个序列进行计算的对齐的点。
那么这条路径我们怎么找到呢?那条路径才是最好的呢?也就是刚才那个问题,怎么样的warping才是最好的。
注明:两个序列长度不同,不能使用欧氏距离进行匹配。使用dtw时,上图方格中的每个连续的点(开头(1,1)和结尾(m,n)还是要保证的)构成的曲线都有可能,这是就要找出代价最小的那条曲线,如图中标出的黑色曲线。
我们把这条路径定义为warping path规整路径,并用W来表示, W的第k个元素定义为wk=(i,j)k,定义了序列Q和C的映射。这样我们有
首先,这条路径不是随意选择的,需要满足以下几个约束:
1)边界条件:w1=(1, 1)和wK=(m, n)。任何一种语音的发音快慢都有可能变化,但是其各部分的先后次序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束。
2)连续性:如果wk-1= (a’, b’),那么对于路径的下一个点wk=(a, b)需要满足 (a-a’) <=1和 (b-b’) <=1。也就是不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。
3)单调性:如果wk-1= (a’, b’),那么对于路径的下一个点wk=(a, b)需要满足0<=(a-a’)和0<= (b-b’)。这限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。
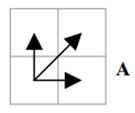
结合连续性和单调性约束,每一个格点的路径就只有三个方向了。例如如果路径已经通过了格点(i, j),那么下一个通过的格点只可能是下列三种情况之一:(i+1, j),(i, j+1)或者(i+1, j+1)。
满足上面这些约束条件的路径可以有指数个,然后我们感兴趣的是使得下面的规整代价最小的路径:
分母中的K主要是用来对不同的长度的规整路径做补偿。我们的目的是什么?或者说DTW的思想是什么?是把两个时间序列进行延伸和缩短,来得到两个时间序列性距离最短也就是最相似的那一个warping,这个最短的距离也就是这两个时间序列的最后的距离度量。在这里,我们要做的就是选择一个路径,使得最后得到的总的距离最小。
这里我们定义一个累加距离cumulative distances。从(0, 0)点开始匹配这两个序列Q和C,每到一个点,之前所有的点计算的距离都会累加。到达终点(n, m)后,这个累积距离就是我们上面说的最后的总的距离,也就是序列Q和C的相似度。
累积距离γ(i,j)可以按下面的方式表示,累积距离γ(i,j)为当前格点距离d(i,j),也就是点qi和cj的欧式距离(相似性)与可以到达该点的最小的邻近元素的累积距离之和:
![]()
注明:先把模板序列和测试序列的每个点相对应的距离算出来,构成一个m xn的矩阵。然后根据每个元素的代价计算一条最短路径。这里的计算要符合以上三个约束。即,一个点的代价=这个点的值+来自min{下、左、斜下这三个方向的值}。下、左、斜下这三个方向的值可以依次递归求得,直到(1,1)点
3 例子
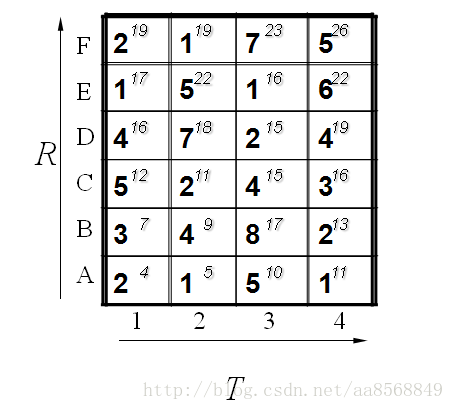
这个例子中假设标准模板R为字母ABCDEF(6个),测试模板T为1234(4个)。R和T中各元素之间的距离已经给出。如下:

既然是模板匹配,所以各分量的先后匹配顺序已经确定了,虽然不是一一对应的。现在题目的目的是要计算出测试模板T和标准模板R之间的距离。因为2个模板的 长度不同,所以其对应匹配的关系有很多种,我们需要找出其中距离最短的那条匹配路径。现假设题目满足如下的约束:当从一个方格((i-1,j-1)或者 (i-1,j)或者(i,j-1))中到下一个方格(i,j),如果是横着或者竖着的话其距离为d(i,j),如果是斜着对角线过来的则是 2d(i,j).其约束条件如下图像所示:
其中g(i,j)表示2个模板都从起始分量逐次匹配,已经到了M中的i分量和T中的j分量,并且匹配到此步是2个模板之间的距离。并且都是在前一次匹配的结果上加d(i,j)或者2d(i,j),然后取最小值。
所以我们将所有的匹配步骤标注后如下:
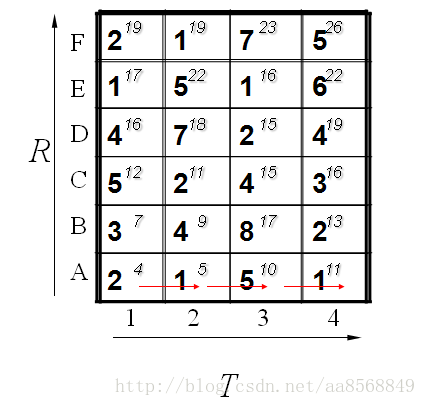
怎么得来的呢?比如说g(1,1)=4, 当然前提都假设是g(0,0)=0,就是说g(1,1)=g(0,0)+2d(1,1)=0+2*2=4.
g(2,2)=9是一样的道理。首先如果从g(1,2)来算的话是g(2,2)=g(1,2)+d(2,2)=5+4=9,因为是竖着上去的。
如果从g(2,1)来算的话是g(2,2)=g(2,1)+d(2,2)=7+4=11,因为是横着往右走的。
如果从g(1,1)来算的话,g(2,2)=g(1,1)+2*d(2,2)=4+2*4=12.因为是斜着过去的。
综上所述,取最小值为9. 所有g(2,2)=9.
当然在这之前要计算出g(1,1),g(2,1),g(1,2).因此计算g(I,j)也是有一定顺序的。
其基本顺序可以体现在如下:
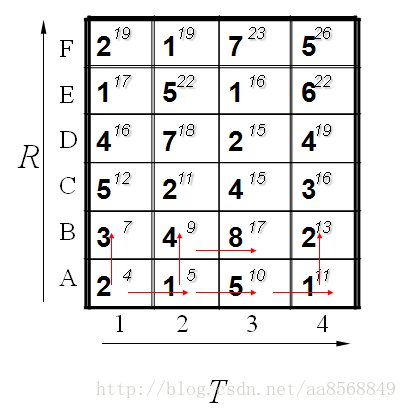
计算了第一排,其中每一个红色的箭头表示最小值来源的那个方向。当计算了第二排后的结果如下:
最后都算完了的结果如下:
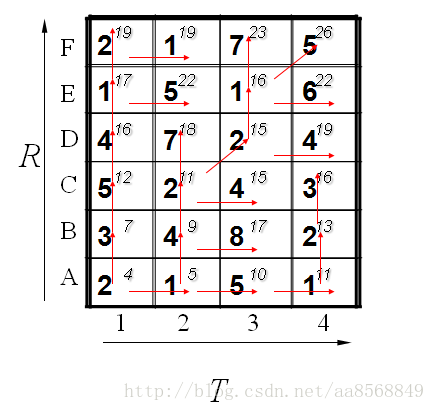
到此为止,我们已经得到了答案,即2个模板直接的距离为26. 我们还可以通过回溯找到最短距离的路径,通过箭头方向反推回去。如下所示:
注明:不管哪个方向,我都只加上了其本身的数值,即d(i j),没有x2.得出的路径是一样的。
4 matlab程序
(待续)
感谢http://blog.csdn.net/zouxy09/article/details/9140207和http://www.cnblogs.com/tornadomeet/archive/2012/03/23/2413363.html两位原作者
以上就是DTW的基本原理啦,上面我一个疑问就是为什么斜下方向过来的是加2*d,左边后下边过来的是加1*d?
我编写的C代码如下: 计算的就是文章里举的例子
C代码如下
//
// main.c
// DTW
//
// Created by 许湘扬 on 16/12/22.
// Copyright (c) 2016年 许湘扬. All rights reserved.
//
#include //最下面一横
{
*(g+(n-1)*m+i)=*(g+(n-1)*m+i-1)+*(p+(n-1)*m+i);
(pr+(n-1)*m+i)->frontI=n-1;
(pr+(n-1)*m+i)->frontJ=i-1;
}
for (int i=n-2; i>=0; i--)//最左边的一竖
{
*(g+i*m+0)=*(g+(i+1)*m+0)+*(p+i*m+0);
(pr+i*m+0)->frontI=i+1;
(pr+i*m+0)->frontJ=0;
}
//计算剩余网格的G值
for (int i=n-2; i>=0; i--)
{
for (int j=1; jint left,under,incline;
left=*(g+i*m+j-1)+*(p+i*m+j);
under=*(g+(i+1)*m+j)+*(p+i*m+j);
incline=*(g+(i+1)*m+j-1)+(*(p+i*m+j))*2;
//从左、下、斜三个方向选出最小的
int min=left;
*(g+i*m+j)=min;
(pr+i*m+j)->frontI=i;
(pr+i*m+j)->frontJ=j-1;
if (min>under)
{
min=under;
*(g+i*m+j)=min;
(pr+i*m+j)->frontI=i+1;
(pr+i*m+j)->frontJ=j;
}
if (min>incline)
{
min=incline;
*(g+i*m+j)=min;
(pr+i*m+j)->frontI=i+1;
(pr+i*m+j)->frontJ=j-1;
}
}
}
//输出G数组
for (int i=0; ifor (int j=0; jprintf("%d\t",*(g+i*m+j));
}printf("\n");
}
//输出方向数组
for (int i=0; ifor (int j=0; jprintf("(%d,%d)\t",(pr+i*m+j)->frontI,(pr+i*m+j)->frontJ);
}printf("\n");
}
}
void printPath(struct pointOritation *po,int n,int m,int *g)
{
//从最后一个点向前输出路径节点
int i=0,j=m-1;
while (1)
{
int ii=(po+i*m+j)->frontI,jj=(po+i*m+j)->frontJ;
if(i==0 && j==0)
break;
printf("(%d,%d):%d\n",i,j,*(g+i*m+j));
i=ii;
j=jj;
}
}
int main()
{
int d[6][4]={
{2,1,7,5},
{1,5,1,6},
{4,7,2,4},
{5,2,4,3},
{3,4,8,2},
{2,1,5,1},
};
int g[6][4];
struct pointOritation pOritation[6][4];//用来存放
gArray(*d,6,4,*g,*pOritation);
printPath(*pOritation, 6, 4,*g);
} PS:考虑到日后的处理的都是很大的数据,所以传递二维数组我都是传的指针,大家可以看一下谭浩强的C语言的书,查看一下二维数组的指针如何使用,以及如何当参数传递,书上面讲的很清楚