目录
- 一.基于度量来分析自己的程序结构
- 第一次作业
- 整体思路介绍
- 第二次作业
- 整体思路介绍
- 第三次作业
- 整体思路介绍
- 第一次作业
- 二.分析自己程序的bug
- 第一次作业
- 第二次作业
- 第三次作业
- 三.发现别人程序bug所采用的策略和一点感受
- 怎么找Bug?
- 我发现的Bug以及三次三种组别的体会
- 四. Applying Creational Pattern
- 初试接口
- 总结
一.基于度量来分析自己的程序结构
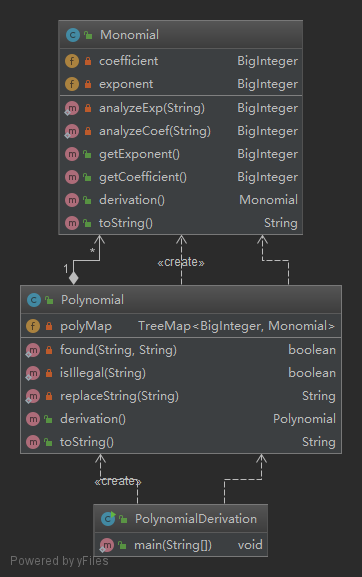
第一次作业
第一次作业的主题是简单多项式导函数的求解,其实也就是幂函数$ax^b$ 的导函数求解。
整体思路介绍
- 第一次作业整体来说较为简单,花费的总时长在4个小时左右。
- 本次设计只涉及幂函数的求导,所以抽象出单项式和多项式两个类。单项式表示的是幂函数,包含系数和指数
- 多项式是很多单项式的集合,使用
TreeMap存储,用指数作为键值key,方便优化以合并同类项。 - 满分小trick:多项式
toString()遍历输出是,把系数为正的项放在最前面
类图
度量分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Monomial.Monomial(BigInteger,BigInteger) | 1 | 1 | 1 |
| Monomial.Monomial(Monomial,Monomial) | 1 | 1 | 1 |
| Monomial.Monomial(String) | 1 | 1 | 1 |
| Monomial.analyzeCoef(String) | 1 | 2 | 3 |
| Monomial.analyzeExp(String) | 1 | 4 | 4 |
| Monomial.derivation() | 2 | 2 | 2 |
| Monomial.getCoefficient() | 1 | 1 | 1 |
| Monomial.getExponent() | 1 | 1 | 1 |
| Monomial.toString() | 1 | 6 | 6 |
| Polynomial.Polynomial() | 1 | 1 | 1 |
| Polynomial.Polynomial(String) | 1 | 4 | 4 |
| Polynomial.derivation() | 1 | 2 | 2 |
| Polynomial.found(String,String) | 1 | 1 | 1 |
| Polynomial.isIllegal(String) | 7 | 2 | 9 |
| Polynomial.replaceString(String) | 1 | 1 | 1 |
| Polynomial.toString() | 1 | 5 | 6 |
| PolynomialDerivation.main(String[]) | 1 | 1 | 1 |
| Class | OCavg | WMC |
|---|---|---|
| Monomial | 2.22 | 20 |
| Polynomial | 3.29 | 23 |
| PolynomialDerivation | 1 | 1 |
优点:
- 结构基本清晰,扩展性好,单项式这个类一直复用到第三次作业
- 优化到位,把正项放在最前面输出,可以节约一个加号,并且合并了同类项
- 基本做到了高内聚,低耦合,也就是老师上课说的“自己的东西自己拿着,不能给别人”
缺点:
- 缺少专门对于输入处理的
InputHandler类 - 对于WRONG FORMAT判断忽略了几个地方,导致出现Bug
- 没有判断
hasNextLine(),虽然不会出现Bug但是鲁棒性不够好
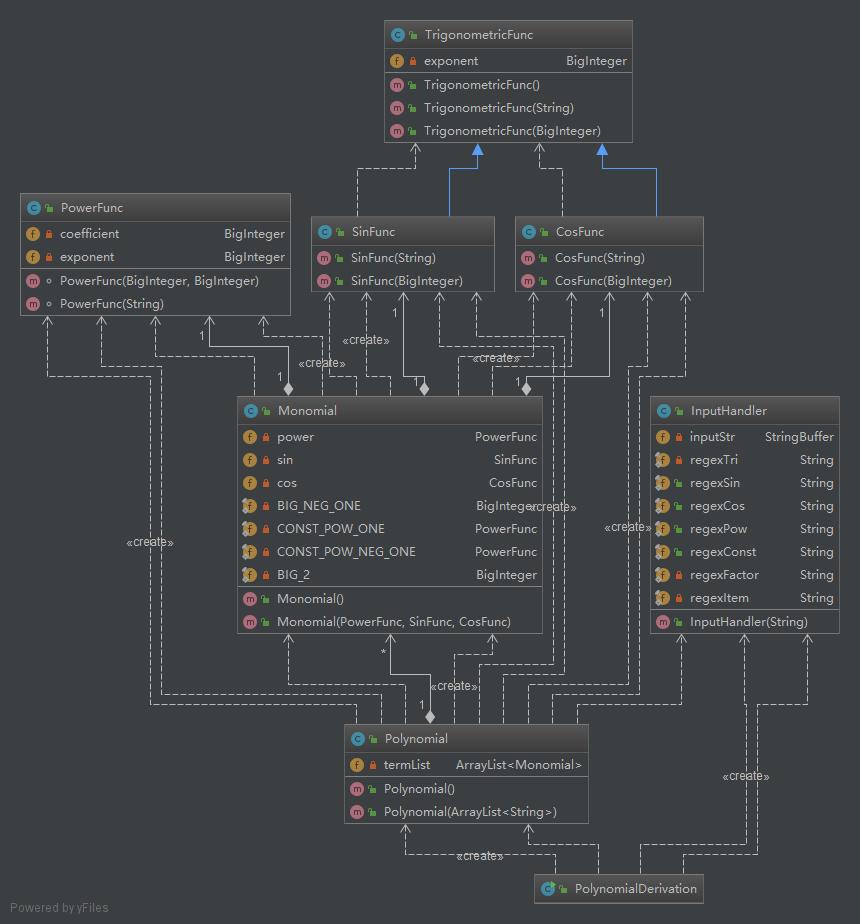
第二次作业
第二次作业的主题是包含简单幂函数和简单正余弦函数的导函数的求解,其实也就是求解形如$ax^bsin^c(x)cos^d(x)$ 类函数的求导问题。
整体思路介绍
类的构造
第二次作业只要提出来一个单项式的基础形式的$ax^bsin^c(x)cos^d(x)$ 解题就简单了。所以PowerFunction类沿用了上次作业的类,并构造了三角函数类,sin类和cos类分别继承自三角函数类
TrigonometricFunc,因为它们的数据和toString()方法是差不多的,只是求导略有不同。这次的单项式类就变成了幂函数、sin、和cos的积单项式求导根据公式,返回一个包含三项的多项式,再将这些项合并得到求导以后的新的多项式,然后合并同类项、提出
sin(x)^2+cos(x)^2=1来化简表达式。为了检索方便,所以采用
ArrayList<>()来保存数据。
类图
度量分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| CosFunc.CosFunc(BigInteger) | 1 | 1 | 1 |
| CosFunc.CosFunc(String) | 1 | 1 | 1 |
| CosFunc.add(BigInteger) | 1 | 1 | 1 |
| CosFunc.add(CosFunc) | 1 | 1 | 1 |
| CosFunc.equals(Object) | 2 | 2 | 2 |
| CosFunc.isSimilar(CosFunc) | 1 | 1 | 1 |
| CosFunc.toString() | 1 | 1 | 1 |
| InputHandler.InputHandler(String) | 1 | 1 | 1 |
| InputHandler.emptyInput() | 1 | 1 | 1 |
| InputHandler.errorFormat() | 1 | 1 | 1 |
| InputHandler.found(String,String) | 1 | 1 | 1 |
| InputHandler.illegalCharacter() | 1 | 1 | 1 |
| InputHandler.stringExtract() | 1 | 9 | 9 |
| Monomial.Monomial() | 1 | 1 | 1 |
| Monomial.Monomial(PowerFunc,SinFunc,CosFunc) | 1 | 1 | 1 |
| Monomial.add(Monomial) | 1 | 1 | 1 |
| Monomial.canMerged(Monomial) | 1 | 5 | 5 |
| Monomial.derivation() | 1 | 1 | 1 |
| Monomial.getCos() | 1 | 1 | 1 |
| Monomial.getPower() | 1 | 1 | 1 |
| Monomial.getSin() | 1 | 1 | 1 |
| Monomial.isSimilar(Monomial) | 1 | 3 | 3 |
| Monomial.mergeWith(Monomial) | 1 | 1 | 1 |
| Monomial.toString() | 3 | 9 | 9 |
| Polynomial.Polynomial() | 1 | 1 | 1 |
| Polynomial.Polynomial(ArrayList) | 1 | 7 | 7 |
| Polynomial.derivation() | 1 | 2 | 2 |
| Polynomial.merge() | 1 | 9 | 9 |
| Polynomial.toString() | 1 | 6 | 6 |
| PolynomialDerivation.main(String[]) | 1 | 2 | 2 |
| PowerFunc.PowerFunc(BigInteger,BigInteger) | 1 | 1 | 1 |
| PowerFunc.PowerFunc(String) | 1 | 1 | 1 |
| PowerFunc.add(PowerFunc) | 1 | 1 | 1 |
| PowerFunc.analyzeCoef(String) | 1 | 2 | 3 |
| PowerFunc.analyzeExp(String) | 1 | 4 | 4 |
| PowerFunc.derivation() | 2 | 2 | 2 |
| PowerFunc.equals(Object) | 3 | 4 | 4 |
| PowerFunc.getCoefficient() | 1 | 1 | 1 |
| PowerFunc.getExp() | 1 | 1 | 1 |
| PowerFunc.isSimilar(PowerFunc) | 1 | 1 | 1 |
| PowerFunc.multiply(PowerFunc) | 1 | 1 | 1 |
| PowerFunc.toString() | 1 | 6 | 6 |
| SinFunc.SinFunc(BigInteger) | 1 | 1 | 1 |
| SinFunc.SinFunc(String) | 1 | 1 | 1 |
| SinFunc.add(BigInteger) | 1 | 1 | 1 |
| SinFunc.add(SinFunc) | 1 | 1 | 1 |
| SinFunc.equals(Object) | 2 | 2 | 2 |
| SinFunc.isSimilar(SinFunc) | 1 | 1 | 1 |
| SinFunc.toString() | 1 | 1 | 1 |
| TrigonometricFunc.TrigonometricFunc() | 1 | 1 | 1 |
| TrigonometricFunc.TrigonometricFunc(BigInteger) | 1 | 1 | 1 |
| TrigonometricFunc.TrigonometricFunc(String) | 1 | 2 | 2 |
| TrigonometricFunc.equals(Object) | 3 | 3 | 3 |
| TrigonometricFunc.getExp() | 1 | 1 | 1 |
| TrigonometricFunc.toString(String) | 2 | 2 | 3 |
| Class | OCavg | WMC |
|---|---|---|
| CosFunc | 1.14 | 8 |
| InputHandler | 1.83 | 11 |
| Monomial | 1.64 | 18 |
| Polynomial | 4.8 | 24 |
| PolynomialDerivation | 2 | 2 |
| PowerFunc | 2.08 | 25 |
| SinFunc | 1.14 | 8 |
| TrigonometricFunc | 1.83 | 11 |
优点:
- 采用了InputHandler统一处理输入,包括格式判断、单项式切割
- 学习了第一次作业互测时别人的代码,判断WRONG FORMAT的方法是:匹配出符合标准的式子就这部分从字符串中删除,判断最后是否是空串
- 运用了继承的思想,提高了代码的复用性
- 优化效果较好:
- 合并了同类项
- 提出了$sin(x)^2+cos(x)^2$ ,将2项化简为1项,减小了长度
缺点:
- 粗心大意,合并同类项写了个Bug,但是自己测试和中测都没有测试出来
- 扩展性不够好,面向对象的思想运用不够到位
- 合并同类项的方法名较为混乱,有的返回新的对象有的是修改原有对象,有加法有乘法,导致出错
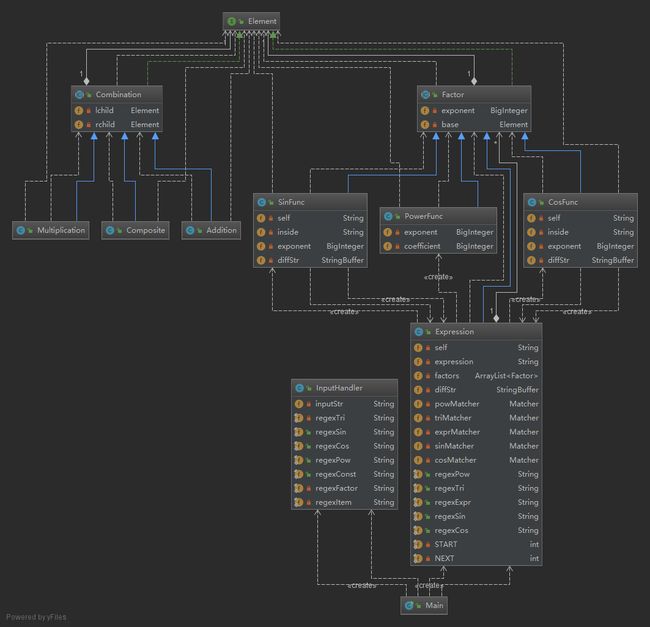
第三次作业
第三次作业的主题是包含简单幂函数和简单正余弦函数的导函数的求解,也就是在第二次作业的基础上,要求支持嵌套求导。
整体思路介绍
第三次作业我个人感觉难度较大。本来想实现表达式树,但是自己思考了很久仍然没有很好的处理办法。最后是学习同学的做法,边解析字符串边求导,所有数据使用字符串保存。
- 建立一个统一的接口,实现求导
derivation()和获得它本身getIt()两个方法 - 建立两个抽象类,一个是组合规则
Combination,一个是因子类Factor - 乘法、加法、复合三种组合规则继承自组合类(最后没有用上)
- 幂函数
PowerFunc因子、sin/cos因子、表达式Expression因子继承自因子类,实现每个因子的求导方法,方便调用 - 把字符串看作一个表达式,用
ArrayList<>()存储Factors,一边解析一边求导
类图
度量分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| InputHandler.InputHandler(String) | 1 | 1 | 1 |
| InputHandler.emptyInput() | 1 | 1 | 1 |
| InputHandler.errorFormat() | 1 | 1 | 1 |
| InputHandler.found(String,String) | 1 | 1 | 1 |
| InputHandler.illegalCharacter() | 1 | 1 | 1 |
| InputHandler.illegalIndex() | 3 | 2 | 3 |
| InputHandler.illegalOp() | 1 | 2 | 2 |
| InputHandler.illegalSpace() | 1 | 2 | 2 |
| InputHandler.stringExtract() | 1 | 7 | 7 |
| InputHandler.unMatchedBrackets() | 1 | 1 | 4 |
| Main.main(String[]) | 1 | 2 | 2 |
| nohair.Addition.Addition(Element,Element) | 1 | 1 | 1 |
| nohair.Addition.derivation() | 1 | 1 | 1 |
| nohair.Addition.getIt() | 1 | 1 | 1 |
| nohair.Addition.toString() | 1 | 1 | 1 |
| nohair.Combination.Combination(Element,Element) | 1 | 1 | 1 |
| nohair.Combination.derivation() | 1 | 1 | 1 |
| nohair.Combination.getIt() | 1 | 1 | 1 |
| nohair.Combination.getLchild() | 1 | 1 | 1 |
| nohair.Combination.getRchild() | 1 | 1 | 1 |
| nohair.Combination.setLchild(Element) | 1 | 1 | 1 |
| nohair.Combination.setRchild(Element) | 1 | 1 | 1 |
| nohair.Combination.toString() | 1 | 1 | 1 |
| nohair.Composite.Composite(Element,Element) | 1 | 1 | 1 |
| nohair.Composite.derivation() | 1 | 1 | 1 |
| nohair.Composite.getIt() | 1 | 1 | 1 |
| nohair.Composite.toString() | 1 | 1 | 1 |
| nohair.CosFunc.CosFunc(BigInteger,Element) | 1 | 1 | 1 |
| nohair.CosFunc.CosFunc(String) | 1 | 2 | 2 |
| nohair.CosFunc.derivation() | 1 | 8 | 8 |
| nohair.CosFunc.errorFormat() | 1 | 1 | 1 |
| nohair.CosFunc.getInsideType() | 1 | 4 | 5 |
| nohair.CosFunc.getIt() | 1 | 1 | 1 |
| nohair.CosFunc.toString() | 1 | 1 | 1 |
| nohair.Expression.Expression(String) | 1 | 1 | 1 |
| nohair.Expression.checkEmpty() | 1 | 2 | 2 |
| nohair.Expression.derivation() | 1 | 15 | 16 |
| nohair.Expression.errorFormat() | 1 | 1 | 1 |
| nohair.Expression.findBrackets(String) | 3 | 5 | 13 |
| nohair.Expression.getIt() | 1 | 1 | 1 |
| nohair.Expression.getString() | 1 | 3 | 3 |
| nohair.Expression.makeDiff(char) | 1 | 11 | 11 |
| nohair.Expression.simplify() | 1 | 2 | 2 |
| nohair.Expression.toString() | 1 | 1 | 1 |
| nohair.Expression.updateMatcher() | 1 | 1 | 1 |
| nohair.Factor.Factor(BigInteger,Element) | 1 | 1 | 1 |
| nohair.Factor.derivation() | 1 | 1 | 1 |
| nohair.Factor.getBase() | 1 | 1 | 1 |
| nohair.Factor.getExp() | 1 | 1 | 1 |
| nohair.Factor.getIt() | 1 | 1 | 1 |
| nohair.Factor.setBase(Element) | 1 | 1 | 1 |
| nohair.Factor.setExponent(BigInteger) | 1 | 1 | 1 |
| nohair.Factor.toString() | 1 | 1 | 1 |
| nohair.Multiplication.Multiplication(Element,Element) | 1 | 1 | 1 |
| nohair.Multiplication.derivation() | 1 | 1 | 1 |
| nohair.Multiplication.getIt() | 1 | 1 | 1 |
| nohair.Multiplication.toString() | 1 | 1 | 1 |
| nohair.PowerFunc.PowerFunc(BigInteger,BigInteger) | 1 | 1 | 1 |
| nohair.PowerFunc.PowerFunc(BigInteger,BigInteger,Element) | 1 | 1 | 1 |
| nohair.PowerFunc.PowerFunc(String) | 1 | 1 | 1 |
| nohair.PowerFunc.analyzeCoef(String) | 1 | 2 | 3 |
| nohair.PowerFunc.analyzeExp(String) | 1 | 4 | 4 |
| nohair.PowerFunc.derivation() | 2 | 2 | 2 |
| nohair.PowerFunc.getCoef() | 1 | 1 | 1 |
| nohair.PowerFunc.getExp() | 1 | 1 | 1 |
| nohair.PowerFunc.getIt() | 1 | 1 | 1 |
| nohair.PowerFunc.toString() | 1 | 6 | 6 |
| nohair.SinFunc.SinFunc(BigInteger,Element) | 1 | 1 | 1 |
| nohair.SinFunc.SinFunc(String) | 1 | 2 | 2 |
| nohair.SinFunc.derivation() | 1 | 8 | 8 |
| nohair.SinFunc.errorFormat() | 1 | 1 | 1 |
| nohair.SinFunc.getInsideType() | 1 | 4 | 5 |
| nohair.SinFunc.getIt() | 1 | 1 | 1 |
| nohair.SinFunc.toString() | 1 | 1 | 1 |
| Class | OCavg | WMC |
|---|---|---|
| InputHandler | 1.7 | 17 |
| Main | 2 | 2 |
| nohair.Addition | 1 | 4 |
| nohair.Combination | 1 | 8 |
| nohair.Composite | 1 | 4 |
| nohair.CosFunc | 2.57 | 18 |
| nohair.Expression | 3.82 | 42 |
| nohair.Factor | 1 | 8 |
| nohair.Multiplication | 1 | 4 |
| nohair.PowerFunc | 2.1 | 21 |
| nohair.SinFunc | 2.57 | 18 |
优点:
- 结构还算清晰吧
- 使用了接口、抽象类,方便保管不同的对象,具有面向对象的思维
- 递归求导,实现起来比较简单
缺点:
- 没有实现出表达式树
- 化简的时候没有考虑周全而出错
- 输出数据为了保证正确性,存在很多冗余的括号
- 大部分数据都以字符串保存,复用性极差,很难化简表达式。这一点也不面向对象!!!
二.分析自己程序的bug
总的来说,Bug都是考虑情况不完全或者是粗心大意造成的。
说到底还是自己的测试不够完全,过于依赖中测而自己测试不够全面
第一次作业
这次虽然强测满分,但是仍存在两个Bug
- 在判断“符号整数存在空格”这一非法情况是,忽略了指数存在符号且与数字部分存在空格这一非法情况,导致诸如
+3*x ^ + 123这种非法情况也会正常计算。 - 关于项的正则表达式存在漏洞,改进后的算法是每一项前必须有一个符号(如果第一项最前面没有符号则添加一个符号),才能正确匹配,即把正则表达式
[+-]?regexPow更改为[+-]regexPow,否则诸如+x x这种情况仍能正确输出。
这是两个没有考虑完全导致的Bug,最难受的是我被Hack了17次,而Bug修复阶段对“合并修复”以及“非合并修复”的理解存在偏差,导致提交了非合并修复是的被扣了17分。吃一堑长一智,以后要好好注意啊!
第二次作业
这次的Bug纯粹是写代码太过粗枝大叶+测试不充分导致的
- 合并同类项(即x, sin(x), cos(x)的指数均相同的项)时,本应只相加幂函数部分的系数,结果不小心把sin(x)和cos(x)的指数也相加了,犯了个非常低级的错误。
由于学习了互测屋中其他同学的第一次作业,采用了删除最后看字符串是否为空的方法,没有了WRONG FORMAT错误,但是这个合并同类项时产生的致命错误导致强测直接爆炸,只有70多分。Bug修复阶段直接注释了两行多余的方法就完成了。
这说明了提交前自己进行充分测试的必要性!!!!!!
第三次作业
这次出现了WRONG FORMAT错误,以及化简导致的错误。
- 由于解析字符串是采用一个类似于状态机的方式,根据符号来判断是否求导,最后没有判断读取到符号以后是否还存在因子,即形如
1*x +这种形式的错误表达式不会被判为"WRONG FORMAT"。所以在解析到因子再判断后面的符号以后,要检查符号+-*后面的子串是否是空串。 - 化简不仅没有得分,还给自己造成了很多Bug。比如化简的时候想去除
1*的因子,结果会造成比如cos(x)^1*sin(x)这样的表达式被错误的化简。这归根结底是没有考虑清楚可以化简的情况使得正则表达式出错。所以这种情况的正则表达式应该修改为"[+-*\(]1\*"
错误的化简导致出错。以后还是求稳比较好,毕竟安全性和正确性是优先于性能的。
三.发现别人程序bug所采用的策略和一点感受
怎么找Bug?
学习了讨论区编写测试脚本的方法,我采用如下的方式来发现别人的Bug:
- 把所有人的代码编译打包为.jar文件
- 编写测试数据(人工或自动生成),保存在
testData.txt文件中 - 编写bash脚本,在Windows平台使用
Git bash执行 - 编写Python脚本
sympy用来计算标准答案,以及互测屋所有输出的答案 - 将第三步和第四步的数据输出保存到
log.txt文件中,人工比对
使用到的工具包括:Python Sympy, Git bash, VS code等。
bash脚本的整体架构如下:
touch $result
cat $inputfile | while read line
do
echo "">>$result
echo "input: $line">>$result
echo "$line" | python getDiff.py>>$result
echo "==================================">>$result
echo "$alterego">>$result
echo "$line" | java -jar $alterego>>$result
echo "$line" | java -jar $alterego | python getAns.py>>$result
echo "----------------------------------">>$result
#############此处省略相同的内容###################
donePython 脚本如下:
# getAns.py
from sympy import *
from sympy.abc import x
if __name__ == "__main__":
formula = input()
formula = formula.replace("^", " ** ")
x = Symbol('x')
fx = sympify(formula)
res = fx.subs('x', 10.0)
print(res)最终得到的的数据如下所示:
input: 1*x^1-sin(cos(x)^1)^1
diff: sin(x)*cos(cos(x)) + 1
value: 0.636510163539491
==================================
Alterego.jar
(1-cos(cos(x)^1)*((-sin(x)*((1)))))
0.636510163539491
----------------------------------
Saber.jar
-(-sin(x)*cos(cos(x)^1))+1
0.636510163539491
----------------------------------
Lancer.jar
+(+(0)*(x^1)+(1*x^0)*(1))-(+(1*sin((cos((x^1))^1))^0*cos((cos((x^1))^1))*(-1*cos((x^1))^0*sin((x^1))*(1*x^0))))
0.636510163539491
----------------------------------
Archer.jar
WRONG FORMAT!
----------------------------------
Rider.jar
WRONG FORMAT!
----------------------------------
Caster.jar
((((0)*(x^1))+((1)*(1)))+(((((-1*cos(cos(x)^1)^1))*((1*sin(cos(x)^1)^0))))*(-1*sin(x))))
0.636510163539491
----------------------------------
Assassin.jar
+1*1+1*sin(cos(x))^0*cos(cos(x))*cos(x)^0*sin(x)*1
0.636510163539491
----------------------------------
Berserker.jar
WRONG FORMAT!
1*
----------------------------------这种半自动化的黑盒测试能大大提高互测的效率。
但这样的互测并不代表不存在任何弊端。
这样的互测省略了读别人代码的环节,是一种纯粹依靠喂数据来发现bug的行为。可能这种形式的互测有些背离这门课互测的初衷了吧。我觉得互测应该是:阅读别人的代码、了解别人的解题思路、从而提升自己的水平,防止自己下次犯同样的错误。
我发现的Bug以及三次三种组别的体会
三次作业我分别进入了A, C, B组,从代码质量可以看得出来三组之间的代码质量的差距非常巨大。
- 第一次作业,A组。我是本组第一个被找到Bug的(被集火17刀),也是这组找Bug最少的(只找到2个,因为当时还没有半自动测试脚本)。所以认真阅读了屋子里的代码,在学习了别人的做法,也找到了别人的正则表达式的漏洞,帮助对我第二次作业的正则表达式有很大的帮助。
- 第二次作业,C组。有了测试脚本的加持,我成了这组最“狼”的人,Hack了17次,甚至一组数据hack了5/6(7人间)。后来翻开代码看了看,与第一次A组的差距非常大,有很多非常明显和低级的错误(当然,我也是犯了低级错误进入了C组)。
- 第三次作业,B组。整体的代码水平都挺好的。这里总共找了10个Bug,问题大多出现在小的、短的表达式上,比如
1*x^1都有朋友输出错误。
这三次的互测后,我相对现在的互测制度提一点小小的建议:
- 仍然划分A, B, C三档,但是分组把这三组混合编组,例如8人间可以{2A, 3B, 3C},7人间{2A, 3B, 2C}
- 找到某个等级的Bug得对应等级得分,而与自己得分数无关
- 这样做得好处是:每个人都可以看到不同水平的代码,给C组和B组的同学更多学习的机会;避免了高段位“大眼瞪小眼”的尴尬,还有低段位“菜鸡互啄”的无趣;找到高段位的Bug更有成就感和分数奖励
- 缺点是:规则较为复杂,助教实现起来可能比较麻烦,而且不一定每个人都接受这种制度
有同学说:“经过这三次互测,我的bash脚本和Python 写的比原来好多了。”
当然,这些都只是我个人的想法,抛砖引玉,还请助教组学长学姐和老师们能研究出更好的制度,回归互测的本质。
四. Applying Creational Pattern
初试接口
继承很好理解,但是接口这一全新的概念着实让人摸不着头脑,显得比较抽象。
下面摘录一段来自讨论区的话:
类继承关系,应当用于主干的逻辑关系
接口可以任意跨越多个继承层次,通过接口获得归一化的数据处理能力。
接口及其实现其实就两个层次,对于实现接口的类没有任何额外的要求,包括数据和原有的方法,只要实现相应接口即可。因为在这种归一化处理下,只会使用接口所定义的方法。换句话说,可以任意跨越多个继承层次,通过接口获得归一化处理能力。
在第三次作业中应用了继承、接口、抽象类等Java语言的特征。抽象父类实现了数据的统一管理,接口将每种因子和组合类型的求导方法统一地管理起来。
Java语言有很多著名的设计模式,课上的PPT也对一些设计模式有介绍。网上可以查阅到很多设计模式的相关资料。这方面需要我加以学习,应用在以后的作业中。
总结
第一单元终于结束了。走了些弯路,花了不少时间
希望以后可以更加面向对象。