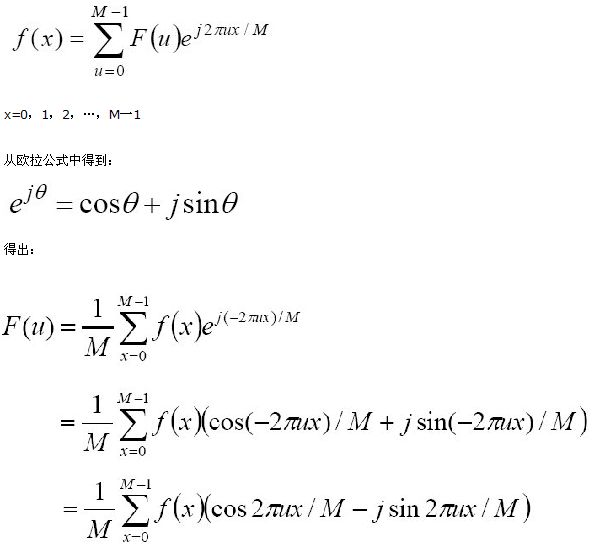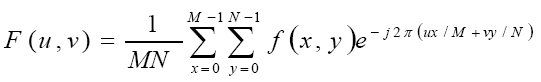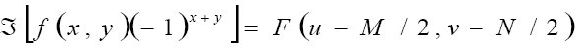傅里叶变换与数字图像处理
转自: http://blog.sina.com.cn/s/blog_8df0c75501015vuw.html
傅里叶变换是将时域信号分解为不同频率的正弦和/余弦和的形式。傅里叶变换是数字图像处理技术的基础,其通过在时域和频域来回切换图像,对图像的信息特征进行提取和分析。
一维傅里叶变换及其反变换
单变量连续函数,f(x)的傅里叶变换F(u)定义为等式:
同样,给出F(u), 能用反DFT来获得原函数:
其中,u=0,1,2,…,M一1。因此,我们看到傅里叶变换的每项[即对于每个u值,F(u)的值由f(x)函数所有值的和组成。f(x)的值则与各种频率的正弦值和余弦值相乘。F(u)值的范围覆盖的域(u的值)称为频率域,因为u决定了变换的频率成分(x也作用于频率,但它们相加,对每个u值有相同的贡献)。F(u)的M项中的每一个被称为变换的频率分量。使用术语“频率域”和“频率成分”与“时间域”和“时间成分”没有差别,如果x是一个时间变量,可以用它来表示f(x)的域和值。
二维DFT及其反变换
一维离散傅里叶变换及其反变换向二 维扩展是简单明了的。一个图像尺寸为M×N的函数f(x,y)的离散傅里叶变换由以下等 式给出:
像在一维中的情形一样,此表达式必须对u值(u=0,1,2,…,M-1)和v值(v=0,1,2,…,N-1)计算。同样,给出F(u,v),可以通过反傅里叶变换获得,f(x,y),由表 达 式给 出:
其中,x=0,1,2,…,M-1,y=0,1,2,…,N-1。变量u和v是变换或频率变量,x和y是空间或图像变量。正如在一维中的情形那样,常量1/MN的位置并不重要,有时它在反变换之前。其他时候,它被分为两个相等的常数1/根号MN,分别乘在变换和反变换的式子前。
定 义傅里叶谱、相角和频率谱:
并且其功率谱为:
其 中,R(u,v)和I(u,v)分别是F(u,v)的实部和虚部。
通 常在进行傅里叶变换之前用(-1)x+y乘以输入的图像函数。由于指数的性质,很容易看出:
其中Ζ[·]表示引文中的傅里叶变换。这个等式说明f(x,y)(-1)x+y傅里叶变换的原点[即F(0,0)]被设置在u =M/2和v=N/2上。换句话说,用(-1)x+y乘以f(x,y)将F(u,v)原点变换到频率坐标下的(M/2;N/2),它是二维DFT设置的M×N区域的中心。我们将此频率域的范围指定为频率矩形,它从u=0到u=M-1从v=0到v=N-1(u和v是整数)。为了确保移动后的坐标为整数,要求M和N为偶数。当在计算机中使用傅里叶变换时,总和的范围为u从1到M,v从1到N。实际的变换中心将为u=(M/2)+1和v=(N/2)十1。
当(u,v)=(0,0)时 的变换值为:
即f(x,y)的平均值。换句话说,如果f(x,y)是一幅图像,在原点的傅里叶变换即等于图像的平均灰度级。因为 在原点处常常为零,F(0,0)有时称做频率谱的直流成分。
了解了傅里叶变化,下面看看为什么要在频率域研究图像增强。
1.可以利用频率成分和图像外表之间的对应关系。一些在空间域表述困难的增强任务,在频率域中变得非常普通。
2.滤波在频率域更为直观,它可以解释空间域滤波的某些性质。
3.可以在频率域指定滤波器,做反变换,然后在空间域使用结果滤波器作为空间域滤波器的指导。
4.一 旦通过频率域试验选择了空间滤波,通常实施都在空间域进行。
在 冈萨雷斯版<数字图像处理>里面的解释就非常的形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它 的光谱或频率谱。同样,傅立叶变换使我们能通过频率成分来分析一个函数。
傅立叶变换在图像处理中有非常非常的作用。因为不仅傅立叶分析涉及图像处理的很多方面,傅立叶的改进算法,比如离散余弦变换,gabor与小波在图像处理中也有重要的分量。傅立叶变换在图像处理以下几个话题都有重要作用:
1.图像增强与图像去噪
绝大部分噪音都是图像 的高频分量,通过低通滤波器来滤除高频——噪声; 边缘也是图像的高频分量,可以通过添加高频分量来增强原始图像的边缘;
2.图像分割之边缘检测
提取图像高频分量
3.图 像特征提取:
形状特征:傅里叶描述子
纹 理特征:直接通过傅里叶系数来计算纹理特征
其他特征:将提取的特征值进行傅里叶变换来使特 征具有平移、伸缩、旋转不变性
4.图像压缩
可以直接通过傅里叶系数来压缩数据;常用的离散余弦变换是傅立叶变换的实变换;
5.信号在频率域的表现
在频域中,频率越大说明原始信号 变化速度越快;频率越小说明原始信号越平缓。当频率为0时,表示直流信号,没有变化。因此,频率的大小反应了信号的变化快慢。高频分量解释信号的突变部分,而低频分量决定信号的整体形象。
在图像处理中,频域反应了图像在空域灰度变化剧烈程度,也就是图像灰度的变化速度,也就是图像的梯度大小。对图像而言,图像的边缘部分是突变部分,变化较快,因此反应在频域上是高频分量;图像的噪声大部分情况下是高频部分;图像平缓变化部分则为低频分量。也就是说,傅立叶变换提供另外一个角度来观察图像,可以将图像从灰度分布转化到频率分布上来观察图像的特征。书面一点说就是,傅里叶变换提供了一条从空域到频率自由转换的途径。对图像处理而言,以下概念非常的重要:
图像高频分量:图像突变部分;在某些情况下指图像边缘信息,某些情况下指噪声,更多是两者的混合;
低频分量:图像变化平缓的部分,也就是图像轮廓信息
高通滤波器:让图像使低频分量抑制,高频分量通过
低 通滤波器:与高通相反,让图像使高频分量抑制,低频分量通过
带通滤波器:使图像在某一部分 的频率信息通过,其他过低或过高都抑制
还有个带阻滤波器,是带通的反。
6.图像去噪
图像去噪就是压制图像的噪音部分。因此,如果噪音是高频额,从频域的角度来看,就是需要用一个低通滤波器对图像进行处理。通过低通滤波器可以抑制图像的高频分量。但是这种情况下常常会造成边缘信息的抑制。常见的去噪模板有均值模板,高斯模板等。这两种滤波器都是在局部区域抑制图像的高频分量,模糊图像边缘的同时也抑制了噪声。还有一种非线性滤波-中值滤波器。中值滤波器对脉冲型噪声有很好的去掉。因为脉冲点都是突变的点,排序以后输出中值,那么那些最大点和最小点就可以去掉了。中值滤波对高斯噪音效果较差。
椒盐噪声:对于椒盐采用中值滤波可以很好的去除。用均值也可以取得一定的效果,但是会引起边缘的模糊。
高 斯白噪声:白噪音在整个频域的都有分布,好像比较困难。
7.图像增强
有时候感觉图像增强与图像去噪是一对矛盾的过程,图像增强经常是需要增强图像的边缘,以获得更好的显示效果,这就需要增加图像的高频分量。而图像去噪是为了消除图像的噪音,也就是需要抑制高频分量。有时候这两个又是指类似的事情。比如说,消除噪音的同时图像的显示效果显著的提升了,那么,这时候就是同样的意思了。
常见的图像增强方法有对比度拉伸,直方图均衡化,图像锐化等。前面两个是在空域进行基于像素点的变换,后面一个是在频域处理。我理解的锐化就是直接在图像上加上图像高通滤波后的分量,也就是图像的边缘效果。对比度拉伸和直方图均衡化都是为了提高图像的对比度,也就是使图像看起来差异更明显一些,我想,经过这样的处理以后,图像也应该增强了图像的高频分量,使得图像的细节上差异更大。同时也引入了一些噪音。
最 后讨论一下图像傅立叶变换的物理意义
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。如:大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值很低;而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域,对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
最后附上傅里叶变换的一个例子。
通过上面的DFT变换可以看到:图像信号能量将集中在系数矩阵的四个角上。这是由二维傅立叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。
经过变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大。