紫薯P229
棋盘覆盖问题
问题描述:
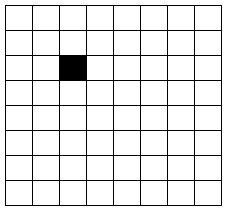
在一个2^k×2^k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何k≥0,有4^k种不同的特殊棋盘.
下图–图(1)中的特殊棋盘是当k=3时16个特殊棋盘中的一个:
图(1)
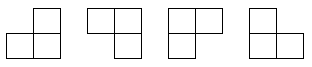
题目要求在棋盘覆盖问题中,要用下图-图(2)所示的4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖.
图(2)
题目包含多组测试数据,输入包含测试数据组数N,下面输入N组数据,每组数据,包括边长m和特殊方格的位置x,y。
input sample
2
2
0 0
8
2 2
output sample
CASE:1
0 1
1 1
CASE:2
3 3 4 4 8 8 9 9
3 2 2 4 8 7 7 9
5 2 0 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
分析:设(x,y)为有棋子的点,则可以将棋盘平均分成四份,(x,y)必在其中的一份,对于其他的三份就可以覆盖分割点处的位置,这样其他的三份也可以看做带棋子的,从而可以递归覆盖
1 #include2 #include 3 using namespace std; 4 const int N = 1000; 5 int q[N][N]; 6 int cnt; 7 // cover的参数分别是棋子的坐标(x,y);棋盘的开始坐标(sx,sy),终点坐标(ex,ey) 8 void cover(int x, int y, int sx, int sy, int ex, int ey) 9 { 10 if (sx == ex && sy == ey) //如果只有一个点,返回 11 return; 12 int tx = ( ex - sx ) / 2 + sx; //求出分割的坐标点 13 int ty = ( ey - sy ) / 2 + sy; 14 if (x <= tx && y <= ty) // 如果棋子在棋盘的左上方 15 { 16 if (ty + 1 <= ey && tx + 1 <= ex) 17 { 18 cnt++; 19 q[tx][ty + 1] = q[tx + 1][ty] = q[tx + 1][ty + 1] = cnt; 20 cover(x, y, sx, sy, tx, ty); 21 cover(tx, ty + 1, sx, ty + 1, tx, ey); 22 cover(tx + 1, ty, tx + 1, sy, ex, ty); 23 cover(tx + 1, ty + 1, tx + 1, ty + 1, ex, ey); 24 } 25 26 } 27 else if (x <= tx && y > ty) // 棋子在棋盘的右上方 28 { 29 if (tx + 1 <= ex && ty + 1 <= ey) 30 { 31 cnt++; 32 q[tx][ty] = q[tx + 1][ty] = q[tx + 1][ty + 1] = cnt; 33 cover(tx, ty, sx, sy, tx, ty); 34 cover(x, y, sx, ty + 1, tx, ey); 35 cover(tx + 1, ty, tx + 1, sy, ex, ty); 36 cover(tx + 1, ty + 1, tx + 1, ty + 1, ex, ey); 37 } 38 } 39 else if (x > tx && y <= ty) //棋子在棋盘的左下方 40 { 41 if (ty + 1 <= ey && tx + 1 <= ex) 42 { 43 cnt++; 44 q[tx][ty] = q[tx][ty + 1] = q[tx + 1][ty + 1] = cnt; 45 cover(tx, ty, sx, sy, tx, ty); 46 cover(tx, ty + 1, sx, ty + 1, tx, ey); 47 cover(x, y, tx + 1, sy, ex, ty); 48 cover(tx + 1, ty + 1, tx + 1, ty + 1, ex, ey); 49 } 50 } 51 else if (x > tx && y > ty) //棋子在棋盘的右下方 52 { 53 if (ty + 1 <= ey && tx + 1 <= ex) 54 { 55 cnt++; 56 q[tx][ty] = q[tx][ty + 1] = q[tx + 1][ty] = cnt; 57 cover(tx, ty, sx, sy, tx, ty); 58 cover(tx, ty + 1, sx, ty + 1, tx, ey); 59 cover(tx + 1, ty, tx + 1, sy, ex, ty); 60 cover(x, y, tx + 1, ty + 1, ex, ey); 61 } 62 } 63 } 64 int main() 65 { 66 int n, t; 67 int x, y; 68 scanf("%d", &t); 69 while (t--) 70 { 71 scanf("%d", &n); 72 scanf("%d%d", &x, &y); 73 cnt = 0; 74 q[x][y] = 0; 75 cover(x, y, 0, 0, n - 1, n - 1); 76 for (int i = 0; i < n; i++) 77 { 78 for (int j = 0; j < n - 1; j++) 79 printf("%d ", q[i][j]); 80 printf("%d\n", q[i][n - 1]); 81 } 82 } 83 return 0; 84 }