OpenGL学习: 光照系列1-光照基础(phong模型)

从本节开始，我们可以开始学习OpenGL中包括光照、模型加载等主题。光照是一个复杂的主题，本节学习简单的Phong reflection model.本节示例程序https://github.com/wangdingqiao/noteForOpenGL/tree/master/lighting。

本节内容整理自: 
1. learnopengl.com Basic Lighting 
2.Modern OpenGL 06 – Diffuse Point Lighting

通过本节可以了解到

• 颜色与光照的关系
• 简单实现的Phong Reflection Model
• Gouraud shading和Phong Shading的对比

颜色与光照的关系

我们看到的物体的颜色，实际上是光照射物体后反射的光进入眼睛后感受到的颜色，而不是物体实际材料的颜色。太阳的白光包含了所有我们可以感知的颜色，可以将这个白光通过棱镜折射后分离为各种颜色的光。一束白光照射到红颜色的车身上，光经过车身，一部分被吸收，一部分被反射进入人的眼睛，我们感知到的颜色就是这个反射后进入眼睛的光的颜色，如下图左所示：

       
图中，红色的表面吸收了蓝色和绿色成分，将红色反射出来。颜色吸收和反射的过程可以表示为： 
LightIntensity∗ObjectColor=Reflectcolor  
计算为: 
(R,G,B)∗(X,Y,Z)=(XR,YG,ZB)  
则上面的过程表示为: 
(1,1,1)∗(1,0,0)=(1,0,0)  
如果将cyan (blue + green) 颜色光束照射到车身，车身会是什么颜色呢？会是黑色的，因为 (0,1,1)∗(1,0,0)=(0,0,0) ,这个过程如上图右所示

如果将cyan (blue + green) 颜色照射到magenta (red + blue) 颜色的表面，那么结果会是什么颜色呢？同理，我们可以得到结果颜色为蓝色

在实际场景中，光的强度的各个分量可以在[0,1]之间变化，材料表面的颜色分量也可以在[0,1]之间变化，例如光照射到一个玩具表面的计算过程为：

glm::vec3 lightColor(0.33f, 0.42f, 0.18f);
glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
glm::vec3 result = lightColor * toyColor; // = (0.33f, 0.21f, 0.06f);
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
   
   
   
   

Phong Reflection Model

要模拟现实的光照是困难的，例如实际光照中，一束光可以经过场景中若干物体反射后，照射到目标物体上，也可以是直接照射到目标物体上。其中经过其他物体反射后再次照射到目标物体上，这是一个递归的过程，将会无比复杂。因此实际模拟光照过程中，总是采用近似模型去接近现实光照。Phong Reflection Model是经典的光照模型，它计算光照包括三个部分：环境光+漫反射光+镜面光，一共三个成分，如下图所示(来自wiki ,作者Brad Smith)： 

环境光成分

环境光是场景中光源给定或者全局给定的一个光照常量，它一般很小，主要是为了模拟即使场景中没有光照时，也不是全部黑屏的效果。场景中总有一点环境光，不至于使场景全部黑暗，例如远处的月亮，远处的光源。 
环境光的实现为：

// 环境光成分
float   ambientStrength = 0.1f;
vec3    ambient = ambientStrength * lightColor * objectColor;
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
   
   
   
   

给定环境光后，场景效果如下图所示： 
 
这里使用了两个着色器绘图。一个着色器用来绘制光源，光源用一个缩小的立方体来模拟，如图中白色立方体所示；另一个着色器用来绘制我们的物体，这里只显示了一个大的立方体。当场景中只有环境光时，立方体只能很暗的显示。

漫反射光成分

漫反射光成分，是光照中的一个主要成分。漫反射光强度与光线入射方向和物体表面的法向量之间的夹角 θ 相关。当 θ  = 0时，物体表面正好垂直于光线方向，这是获得的光照强度最大；当 θ  = 90时物体表面与光线方向平行，此时光线照射不到物体，光的强度最弱；当 θ>90 后，物体的表面转向到光线的背面，此时物体对应的表面接受不到光照。入射角度如下图所示： 

这里需要的向量包括: 
1.光源和顶点位置之间的向量L 需要计算。 
2.法向量N 通过顶点属性里指定 经过模型和视变换后需要重新计算。

作为本节的简单示例程序，我们在顶点属性中指定法向量，例如立方体的正面ABCD这个面的顶点属性如下所示：

// 顶点属性 位置 纹理坐标  法向量
GLfloat vertices[] = {
        -0.5f, -0.5f, 0.5f, 0.0f, 0.0f, 0.0f, 0.0f,1.0f,    // A
        0.5f, -0.5f, 0.5f, 1.0f, 0.0f,  0.0f, 0.0f, 1.0f,   // B
        0.5f, 0.5f, 0.5f,  1.0f, 1.0f,   0.0f, 0.0f, 1.0f,  // C
        0.5f, 0.5f, 0.5f,  1.0f, 1.0f,   0.0f, 0.0f, 1.0f,  // C
        -0.5f, 0.5f, 0.5f,  0.0f, 1.0f,  0.0f, 0.0f, 1.0f,  // D
        -0.5f, -0.5f, 0.5f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f,   // A
    ...省略
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
   
   
   
   

和顶点位置属性一样，我们需要将法向量数据发送到GPU，并且使用glVertexAttribPointer告诉OpenGL数据的解析方式。这些内容在前面已经介绍了，这里不再赘述。

将顶点属性传递到着色器后，需要在着色器中开始我们的光照计算。有两种方法执行向量L和N的计算。一种方式是在世界坐标系中计算，另一种是在相机坐标系中计算，两种方法都可以实现。

在世界坐标系中计算光照

这里以在世界坐标系中计算L和N为例进行说明，在相机坐标系中计算也有类似操作。在世界坐标系中，计算L时，光源lightPos是在世界坐标系中指定的位置，直接使用即可。顶点位置需要变换到世界坐标系中，利用Model矩阵即可，使用式子: 
FragPos=vec3(model∗vec4(position,1.0));(变换后顶点位置)
在计算N时需要注意，我们不能直接利用 Model∗normal 来获取变换后的法向量，应该使用式子: 
Normal=mat3(transpose(inverse(model)))∗normal(变换后法向量) 。
这个式子的具体推导过程，可以参考The Normal Matrix。 
综上所述，顶点着色器中计算顶点位置和法向量代码为：

#version 330
layout(location = 0) in vec3 position;
layout(location = 1) in vec2 textCoord;
layout(location = 2) in vec3 normal;

out vec3 FragPos;
out vec2 TextCoord;
out vec3 FragNormal;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
gl_Position = projection * view * model * vec4(position, 1.0);
FragPos = vec3(model * vec4(position, 1.0)); // 在世界坐标系中指定
TextCoord = textCoord;
mat3 normalMatrix = mat3(transpose(inverse(model)));
FragNormal = normalMatrix * normal; // 计算法向量经过模型变换后值
}
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
    
    
    
    
12
    
    
    
    
13
    
    
    
    
14
    
    
    
    
15
    
    
    
    
16
    
    
    
    
17
    
    
    
    
18
    
    
    
    
19
    
    
    
    
20
    
    
    
    
21
   
   
   
   

在片元着色器中，计算漫反射光成分的代码为：

// 漫反射光成分 此时需要光线方向为指向光源
vec3    lightDir = normalize(lightPos - FragPos);
vec3    normal = normalize(FragNormal);
float   diffFactor = max(dot(lightDir, normal), 0.0);
vec3    diffuse = diffFactor * lightColor * objectColor;
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
   
   
   
   

这里使用max(dot(lightDir, normal), 0.0)主要是为了防止当光线和法向量夹角大于90后，取值为负的情况，因此使用max保证漫反射光照系数在[0.0,1.0]范围内。 
添加了漫反射光成分后的效果如下图所示： 

镜面反射光成分

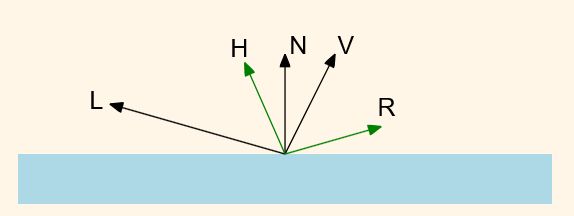
镜面光成分模拟的是物体表面光滑时反射的高亮的光，镜面光反映的通常是光的颜色，而不是物体的颜色。计算镜面光成分时，要考虑光源和顶点位置之间向量L、法向量N、反射方向R、观察者和顶点位置之间的向量V之间的关系，如下图所示(来自:Lighting and Material)： 
 
当R和V的夹角 θ 越小时，人眼观察到的镜面光成分越明显。镜面反射系数定义为: 
specFactor=cos(θ)s  
其中 s 表示为镜面高光系数（shininess ），它的值一般取为2的整数幂，值越大则高光部分越集中，例如下面图中，测试了几种不同的高光系数，效果如下所示： 

计算镜面光成分过程为：

// 镜面反射成分 此时需要光线方向为由光源指出
float   specularStrength = 0.5f;
vec3    reflectDir = normalize(reflect(-lightDir, normal));
vec3    viewDir = normalize(viewPos - FragPos);
float   specFactor = pow(max(dot(reflectDir, viewDir), 0.0), 32); // 32为镜面高光系数
vec3    specular = specularStrength * specFactor * lightColor * objectColor;
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
   
   
   
   

这里需要注意的是，利用reflect函数计算光的出射方向时，要求入射方向指向物体表面位置，因此这里翻转了lightDir，计算为：

   vec3 reflectDir = normalize(reflect(-lightDir, normal));
   
   
   
   

    
    
    
    
1
   
   
   
   

将上述三种光成分叠加后，成为最终物体的颜色，片元着色器中实现为：

   vec3 result = ambient + diffuse + specular 
   color = vec4(result , 1.0f);
   
   
   
   

    
    
    
    
1
    
    
    
    
2
   
   
   
   

绘制效果如下图所示： 

per-vertex 和per-fragment实现光照的对比

上面我们实现的光照计算是在片元着色器中进行的，这种是基于片元计算的，称之为Phong shading。在过去OpenGL编程中实现的是在顶点着色器中进行光照计算,这是基元顶点的计算的，称之为Gouraud Shading。Gouraud Shading和Phong shading，两者的效果对比如下图所示(来自learnopengl.com Basic Lighting)： 

基于顶点计算光照的优势在于顶点数目比片元数目少，因此计算速度快，但是基于顶点计算的光照没有基元片元的真实，主要是顶点计算时，只计算了顶点的光照，而其余片元的光照由插值计算得到，这种插值后的光照显得不是很真实，需要使用更多的顶点来加以完善。例如下面的图中，分别显示了使用少量和大量顶点的基于顶点的光照计算效果:

             

使用基于片元的光照计算时能够获取更为平滑的光照效果。实现基元顶点的光照计算过程，即将上述在片元着色器中的光照计算过程迁移到顶点着色器中执行。

Phong不能处理的情况

我们知道，Phong模型在计算镜面光系数为：

float   specFactor = pow(max(dot(reflectDir, viewDir), 0.0), 32); // 32为镜面高光系数
   
   
   
   

    
    
    
    
1
   
   
   
   

这里的计算由反射向量和观察向量决定，当两者的夹角 θ 超过90时，截断为0.0，则没有了镜面光成分。因此Phong模型能处理的是下面的左图中( θ≤90 )的情况，而对于右图中( θ>90 )的情况则镜面光成分计算为0(来自Advanced-Lighting)。 

而右图的这种情况实际上是存在的，将镜面光成分取为0，没有很好地体现实际光照情况。例如下面的图表示的是，镜面光系数为1.0，法向量为(0.0,1.0,0.0)的平面位置在-0.5,光源在原点时，观察者在(0,0,4.0)位置时，光照展示的情形：

这里我们看到，Phong的镜面光成分，在边缘时立马变暗，这种对比太明显，不符合实际情形。

---

Blinn-Phong

Blinn-Phong模型镜面光的计算，采用了半角向量(half-angle vector)，这个向量是光照向量L和观察向量V的取中向量，如下图所示(来自Blinn-Phong Model)：

计算为:  H=L+V||L+V||

当观察向量与反射向量越接近，那么半角向量与法向量N越接近，观察者看到的镜面光成分越强。

对比Phong和Blinn-Phong计算镜面光系数为：

 vec3   viewDir = normalize(viewPos - fs_in.FragPos);
float   specFactor = 0.0;
if(blinn)  // 使用Blinn-Phong specular 模型
{
vec3 halfDir = normalize(lightDir + viewDir);
specFactor = pow(max(dot(halfDir, normal), 0.0), 32.0); 
}
else    // 使用Phong specular模型
{
vec3    reflectDir = normalize(reflect(-lightDir, normal)); // 此时需要光线方向为由光源指出
specFactor = pow(max(dot(reflectDir, viewDir), 0.0), 8.0); 
}
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
    
    
    
    
12
   
   
   
   

使用半角向量后，保证了半角向量H与法向量N的夹角在90度范围内，能够处理上面对比图中右图所示的情形。下面左是镜面高光系数为0.5时使用Blinn-Phong渲染效果：

      

右图是镜面高光系数为0.5时使用Phong渲染效果:

一般地，使用Blinn-Phong模型时要得到相同强度的镜面光，镜面系数需要为Phong模型的2-4倍，例如Phong模型的镜面高光系数设置为0.8，可以设置Blinn-Phong模型的系数为32.0。

关于Phong和Blinn-Phong模型更多地对比，可以参考Relationship between Phong and Blinn lighting model。

最后的说明

在计算光照的过程中，注意使用的向量一定要单位化，因为 cosθ 值的计算依赖于两个参与点积的向量是单位向量这一事实，否则计算会出错。另外在世界坐标系还是在相机坐标系中进行光照计算都是可以的，这个取决于你的喜好，但是要注意将顶点位置、法向量都变换到同一个坐标系下进行光照计算。

本节实现的Phong reflection model还不够完善，一方面从光源角度看，属于点光源，但是缺少随着距离的衰减；另一方面从物体的材质角度看，没有反映出物体不同部分对光感受的强度不同这一特点，需要使用材质属性加以改进。这些内容将放在下一节中进行学习。