三大抽样分布——卡方分布、t分布、F分布

卡方分布

定义
设$(X_1,X_2,...,X_n)$是来自总体$X\sim N(0,1)$的一个样本，则称统计量：$${\chi }^2=\sum _{i=1}^n{X}_i^2$$所服从的分布是自由度为$n$的卡方(${\chi }^2$)分布，记作${\chi }^2\sim {\chi }^2(n)$。自由度是指独立正态随机变量的个数，它是随机变量分布中的一个重要参数。

卡方随机变量${\chi }^2(n)$的概率密度函数为：$$f_{{\chi }^2}=\{\begin{array}{ll}\frac{1}{2^{\frac{n}{2}}\Gamma (\frac{n}{2})}{x}^{\frac{n}{2}-1}{e}^{-\frac{x}{2}},& \text{x>0}\\ 0,& \text{x⩽0}\end{array}$$其中，$\Gamma (\frac{n}{2})={\int }_0^{\infty }{x}^{\frac{n}{2}-1}{e}^{-x}dx，\Gamma (\frac{1}{2})=\sqrt{\pi }$

卡方分布的性质

1. ${\chi }^2(x,n)⩾0$
2. ${\int }_{-\infty }^{+\infty }{\chi }^2(x,n)dx=1$
3. ${\chi }^2$分布的可加性。设${\chi }_1^2\sim {\chi }^2(n_1)$，${\chi }_2^2\sim {\chi }^2(n_1)$，且${\chi }_1^2$与${\chi }_2^2$相互独立，则：$${\chi }_1^2+{\chi }_2^2\sim {\chi }^2(n_1+n_2)$$
4. 若${\chi }^2\sim {\chi }^2(n)$，则$E({\chi }^2)=n，D({\chi }^2)=2n$

上$\alpha$分位数
设随机变量$X$的分布函数为$F(x)$，对于给定的正数$\alpha (0<\alpha <1)$，若有$x_{\alpha }$满足$$F(x_{\alpha })=P(X⩾x_{\alpha })=\alpha$$则称$x_{\alpha }$为分布$F(x)$的上的$\alpha$分位数(或上$\alpha$分位点)

${\chi }^2$分布上的$\alpha$分位数
对于不同自由度$n$及不同的数$\alpha (0<\alpha <1)$，定义${\chi }_{\alpha }^2$是自由度为$n$的${\chi }^2$分布的上$\alpha$分位数，如果其满足$$P({\chi }^2⩾{\chi }_{\alpha }^2)={\int }_{{\chi }_{\alpha }^2}^{+\infty }{f}_{{\chi }^2}(x)dx=\alpha$$${\chi }^2$分布的上$\alpha$分位数的值可以通过查表得出，当$n$较大($n⩾45$)时，有近似公式$${\chi }_{\alpha }^2\approx \frac{1}{2}(u_0+\sqrt{2n-1}{)}^2$$其中$u_0$为标准正态分布的上$\alpha$分位数

t分布

定义
设$X\sim N(0,1)，Y\sim {\chi }^2(n)$，且$X$与$Y$相互独立，则称统计量：$$T=\frac{X}{\sqrt{\frac{Y}{n}}}$$所服从的分布是自由度为$n$的$t$分布，记为$T\sim t(n)$，$t$分布又称为学生氏分布。

$t$分布的概率密度函数为$$f_T(x)=\frac{\Gamma (\frac{n+1}{2})}{\sqrt{n\pi }\Gamma (\frac{n}{2})}(1+\frac{x^2}{n}{)}^{-\frac{n+1}{2}}，-\infty <x<+\infty$$

t分布图像的性质

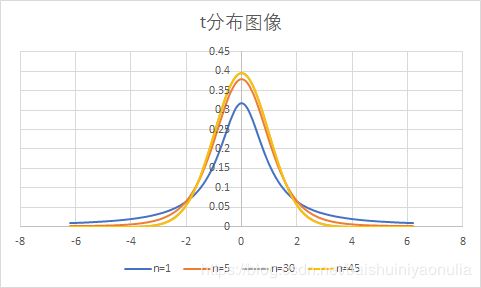
1. 概率密度函数曲线关于$x=0$对称
2. 概率密度函数在$x=0$处达到最大值
3. 概率密度函数曲线的水平渐近线为$x$轴
4. 当自由度$n\to \infty$时，$t$分布将趋于$N(0,1)$

t分布的性质

1. 若$T\sim t(n)$，则当$n>1$时，有$E(T)=0$；当$n>2$时，有$D(T)=\frac{n}{n-2}$
2. 当自由度$n\to \infty$时，$t$分布将趋向于$N(0,1)$
3. 对于不同自由度$n$及不同的数$\alpha (0<\alpha <1)$，若满足$$P(T⩾t_{\alpha })={\int }_{t_{\alpha }}^{+\infty }{f}_T(x)dx=\alpha$$则定义$t_{\alpha }$是自由度为$n$的$t$分布的上$\alpha$分位数。$t_n$分布的上$\alpha$分位数$t_{\alpha }(n)$可查表得出。
4. $t_{\alpha }(n)=t_{1-\alpha }(n)$

F分布

定义
设$X\sim {\chi }^2(n_1)$，$Y\sim {\chi }^2(n_2)$，且$X$与$Y$相互独立，则称统计量$$F=\frac{\frac{X}{n_1}}{\frac{Y}{n_2}}$$服从自由度为$n_1$和$n_2$的$F$分布，记作：$F\sim F(n_1,n_2)$

$F$分布的概率密度函数为：$$f_F=\{\begin{array}{ll}\frac{\Gamma (\frac{n_1+n_2}{2})}{\Gamma (\frac{n_1}{2})\Gamma (\frac{n_2}{2})}{n}_1^{\frac{n_1}{2}}{n}_2^{\frac{n_2}{2}}\frac{x^{\frac{n_1}{2}-1}}{(n_{1}x+n_2{)}^{\frac{n_1+n_2}{2}}},& \text{x>0}\\ 0,& \text{x⩽0}\end{array}$$

$F$分布的性质

1. $F$分布的概率密度函数图像与${\chi }^2$分布的概率密度函数类似，都是只取非负值的偏态分布
2. 对于不同自由度$n_1$和$n_2$及不同的数$\alpha (0<\alpha <1)$，若满足：$$P(F⩾F_{\alpha })={\int }_{F_{\alpha }}^{+\infty }{f}_F(x)dx=\alpha$$定义$F_{\alpha }$是自由度为$n_1$和$n_2$的$F$分布的上$\alpha$分位数。