圆形靶内的最大飞镖数量

题目

1453. 圆形靶内的最大飞镖数量

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。
投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。
请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

数据规模：点的个数N<=100,r<=5000

对题目进行解析，就是要找一个圆心，使得以该圆心为中心、r为半径的圆能够覆盖（在圆内或者圆上）更多的给定的点。求能覆盖的最多的点的数目。

思路

由于圆心是在二维坐标平面，是无限可能的，所以不能直接用暴力的方法。

换一种思路，如果找到这个圆（这个圆能覆盖最多的点），那么一定满足至少有两个点在这个圆上。用反证法可以证明：
如果有0个点在这个圆上，可以通过移动圆心，使得有1个点在圆上，并且被覆盖的点不会变少。
如果有1个点在这个圆上，可以通过移动圆心，使得有2个点在圆上，并且被覆盖的点不会变少。可以通过固定这个点在圆上，然后进行旋转。

所以遍历两两的点，找到他们的圆心，求这个圆心覆盖的点的个数。

从圆上两个点找到圆心的公式是：

实现代码如下：

class Solution {
    double precision=1e-10;
    public int numPoints(int[][] points, int r) {
        int n=points.length;
        int max=1;
        for(int i=0;i2*r){
            return null;
        }
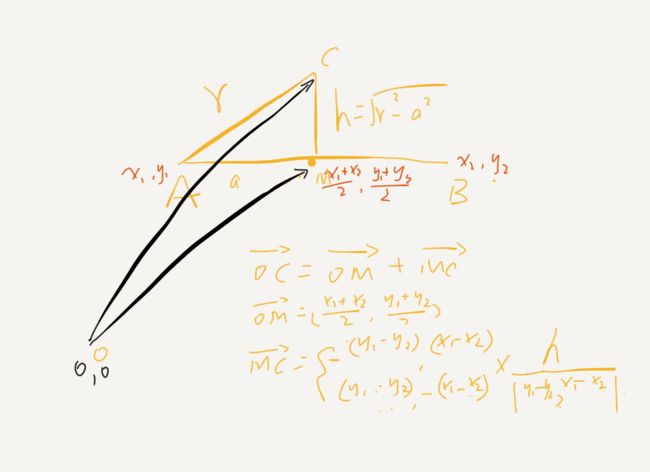
        double a=dist/2;
        double h=Math.sqrt(r*r-a*a);
        double[] OM=new double[]{(p0[0]+p1[0])/2.0,(p0[1]+p1[1])/2.0};
        double[] MC=new double[]{p0[1]-p1[1],-(p0[0]-p1[0])};
        double factor=h/getDist(MC,new double[]{0,0});
        MC[0]*=factor;
        MC[1]*=factor;
        return new double[]{OM[0]+MC[0],OM[1]+MC[1]};
    }

    private double getDist(double[] p1,double[] p2){
        double x=p1[0]-p2[0];
        double y=p1[1]-p2[1];
        return Math.sqrt(x*x+y*y);
    }
}

还有另一种叫做Angular Sweep的算法，以后有空再看看。

参考：
关于为什么一定会有两个点在圆上
Angular Sweep
Angular Sweep