-
前言
小小书生,开始写下小小记录。其实写博客不知天高地厚的分享给朋友,单纯就第一次认真写博客的猎奇行为,可能有人觉得菜和其他莫名其妙的意义等等,也无所谓,大佬们多点包容,菜鸡瑟瑟发抖。
-
冒泡算法(优化) 参考来源
冒泡排序Bubble Sort,顾名思义,就像汽水中常常有许多小小的气泡,哗啦哗啦飘到上面来。这是因为组成小气泡的二氧化碳比水要轻,所以小气泡可以一点一点向上浮动。
考虑下面例子:
在经过几次冒泡后,变成以下状态(紫色为已经排序好的):
再经过一次冒泡后,如下所示:
此时我们可以发现,整个数组已经是有序状态了,接下来的排序都是再做无用功,那么,其实我们在每一轮的冒泡中,可以用一个boolean变量来判断是否产生交换位置过,当没有交换过,我们就可以提前结束排序。
第一版优化代码:
public static void sort(int[] arr) {
int l=arr.length;
for(int i=0;iarr[j+1]){
swap(arr, j, j+1);
//产生交换
isSorted=false;
}
}
if(isSorted){
//没有交换,表明数组已经有序,跳出循环
break;
}
}
}
那么我们接下来继续优化,考虑下面例子:
我们发现,此时经过两轮冒泡后,右边有序区间长度为2(紫色部分),但我们认真看看,可以看到,前面的 3 4 5 6 部分其实已经有序了,实际上右边有序区间长度已经大于2了,但我们却依然接下来冒泡还要进行无意义的比较。那么,怎么避免这种情况呢? 其实,只要在每一轮的冒泡比较中,记录最后一次交换的位置,那么该位置右边的部分必然已经有序。
第二版优化代码:
public static void sort(int[] arr) {
int l=arr.length;
//无序序列的右边界
int border=l-1;
int p=0;
for(int i=0;iarr[j+1]){
swap(arr, j, j+1);
//产生交换
isSorted=false;
p=j;
}
}
border=p;
if(isSorted){
//没有交换,表明数组已经有序,跳出循环
break;
}
}
}
-
快排算法(三分优化)
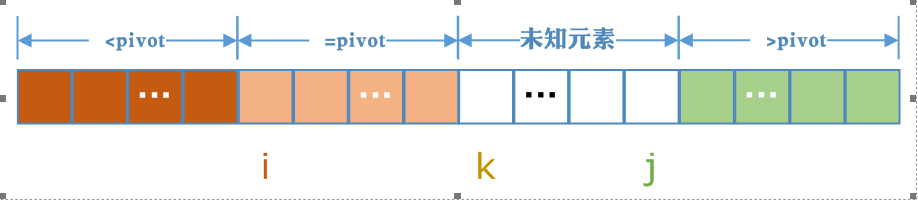
快排算法,是以一个数为基准,将小于等于基准的数放在左边,大于等于基准的数放在右边,以此递归排序的算法。考虑一种情况,就是当大量出现与基准相同的数,其实相等的数没有必要放入左边或者右边部分进行递归。因此,就出现了三分划分的优化方法。三向切分快速排序的基本思想,用i,j,k三个将数组切分成四部分,a[L, i-1]表示小于pivot的部分,a[i, k-1]表示等于pivot的部分,a[j+1]表示大于pivot的部分,而a[k, j]表示未判定的元素(即不知道比pivot大,还是比中轴元素小)。我们要注意a[i]始终位于等于pivot部分的第一个元素,a[i]的左边是小于pivot的部分。
那么初始化的情况就是,i = L,k = L+1,j=R(L表示最左边元素的索引,R表示最右边元素的索引)
在k的扫描过程中我们可以对a[k]分为三种情况讨论
(1)a[k] < pivot 交换a[i]和a[k],然后i和k都自增1,k继续扫描
(2)a[k] = pivot k自增1,k接着继续扫描
(3)a[k] > pivot 这个时候显然a[k]应该放到最右端,但由于我们由于不知道a[j]的大小情况,因此,应该将a[k]与a[j]交换,并且j--,然后重新从a[k]扫描,
三向切分代码:
public static void sort(int[] arr,int l,int r) {
/*省略掉元素长度为0和左边界>=有边界的情况*/
if(l>=r || l<0 || arr==null || arr.length==0){
return;
}
/*取最左边 最右边 中间 的三个数中的中位数为基准*/
int mid=l+(r-l)/2;
if(arr[mid]